第一章：绪论

计算

计算=信息处理
计算：借助某种工具，遵照一定规则，以明确而机械的方法进行
计算模型=计算机=信息处理工具

算法

算法：特定计算模型下，解决特定问题的指令序列

正确性：的确可以解决指定的问题
确定性：基本操作组成的序列
可行性：每一基本操作可实现，可以在常数时间内完成
有穷性：对于任何输入，经过有穷次基本操作可以得到输出；下例

$\begin{align} Hailstone(n)= \left\{ \begin{array}{l} \{1\} ,n\leq1 \\ \{n\} \cup Hailstone(n/2),\ n \ is \ even\\ \{n\} \cup Hailstone(3n+1),\ n \ is \ odd \end{array}\right. \end{align}\\$ $|Hailstone(n)|<\infty \ ?$

int hailstone(int n){
	int len=1;
	while(1<n){
	(n%2)?n=3*n+1;n/=2;
	len++;
	}
	return len;
}

$程序\neq算法$

好的算法

正确性
健壮性
可读
效率：速度快；存储空间尽可能少
- 算法+数据结构=程序

计算模型

性能测度：To measure is to know.

算法分析

正确性
成本：运行时间+所需空间
- 如何进行度量？划分等价类
- 如何划分？问题规模
- 规模接近，计算成本接近；规模增加；计算成本上升
- $T_A(n)=用算法A求解某一问题规模为n的实例$
- 可能存在较好/较坏的情况
- $T_A(n)=用算法A求解某一问题规模为n的实例，T(n)=max\{T(P)||P|=n\}$

理想模型

如何评价针对同一问题多种算法的优劣？

实验统计不准确；采用理想的模型

图灵机模型

tape：分为很多cell，默认均标记为特定符号
alphabet：有限字符表
head：读写头，任何时刻对准某一个cell
state：有限种状态中的某一种；
transition function：状态转移函数；

RAM

无限空间，顺序编号的寄存器：$R[0],R[1],…,R[n]$
每一操作仅需要常数时间
- R[i] <- c
- R[i] <- R[j]
- R[i] <- R[R[j]]
- R[R[i]] <- R[j]
- R[i] <- R[j] +/- R[k]
- IF … GOTO; GOTO; STOP

提供简化的计算工具，独立于平台进行比较合评判

算法的运行时间算法需要执行的基本操作次数

$T(n)$ 算法为求解规模为n的问题，所需执行的基本操作次数

实例：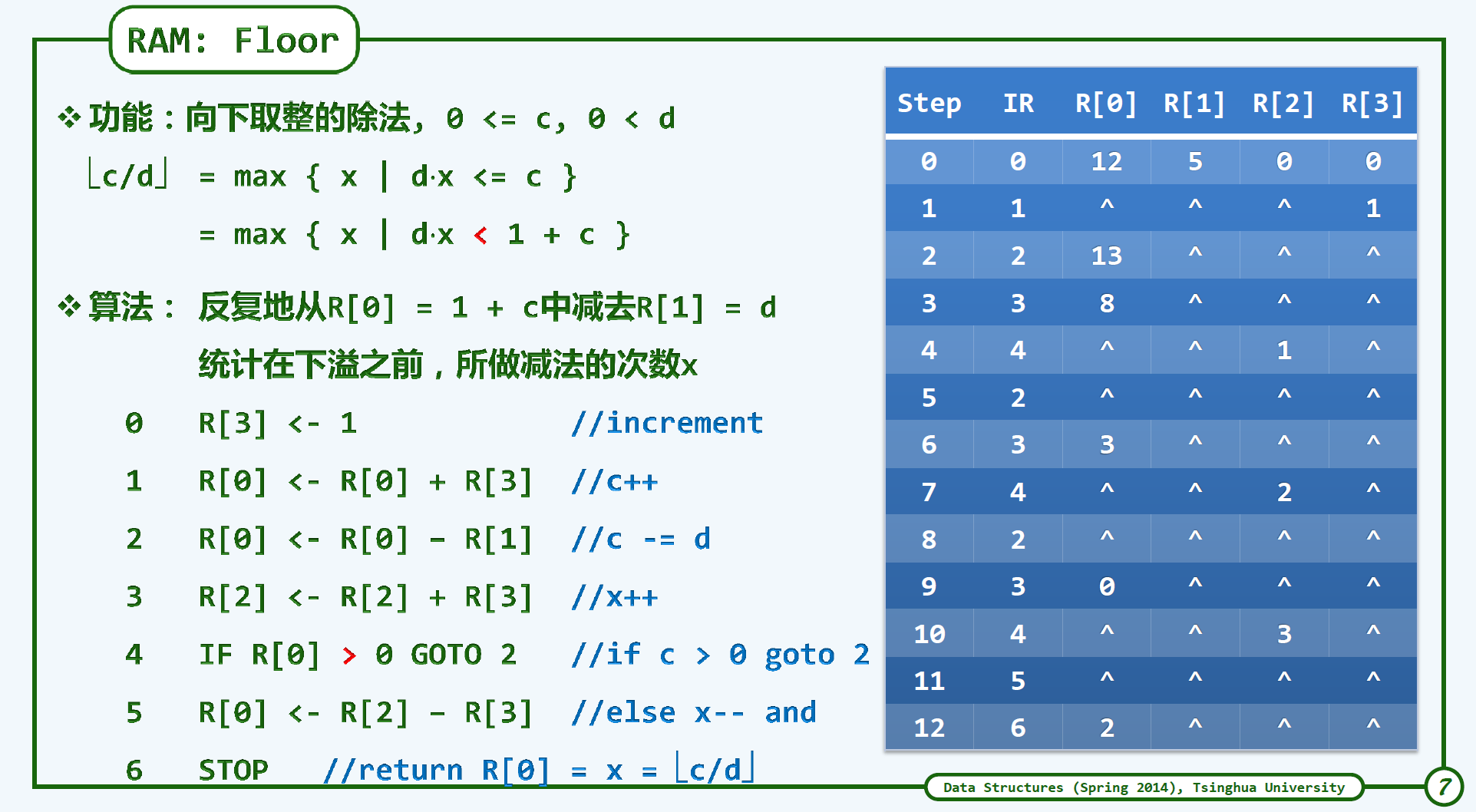

渐进复杂度

将输入规模视作决定计算成本的主要因素

大$O$记号

长远、主流：好读书不求甚解每有会意便欣然忘食

渐进上界定义：$T(n)=\mathcal{O}(f(n)),if\ \exist c>0,n\gg2,T(n) < c\cdot f(n)$

$T(n)$更加简洁，依然能够反映前者的增长趋势

常系数可以忽略 $\mathcal{O}(f(n))=\mathcal{O}(c \cdot f(n))$
低次项可以忽略 $\mathcal{O}(n^a+n^b)=\mathcal{O}(n^a),a>b>0$

大$\Omega$记号

大$\Omega$代表渐进的下界，算法运行的最好情况

大$\Theta$表示算法的确界

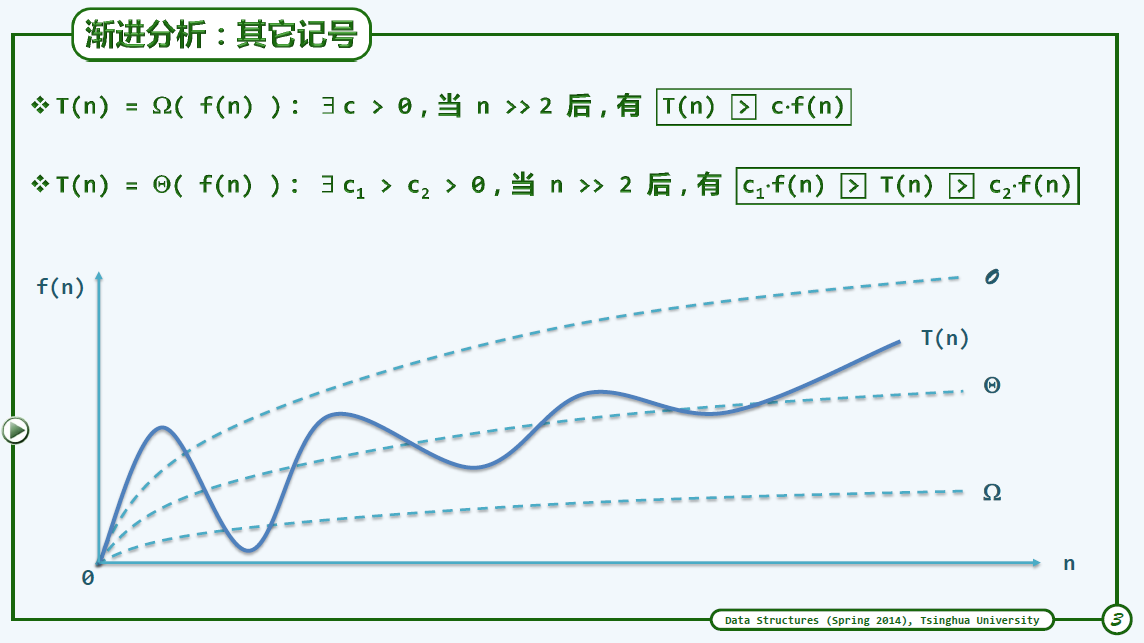
刻度

$\mathcal{O}(1)$
- 常数复杂度
- 甚至包括高阶的常数$2022^{2022}$
- 效率最高
- 特征：不含循环、调用、递归（不严谨
$\mathcal{O}(\log^cn)$
- 常数无所谓（换底公式）
- $n$常数次幂无所谓
- 非常高效，复杂度无限接近于常数
$\mathcal{O}(n^c)$
- 多项式复杂度
- 由多项式中次数最高的项决定
- $\mathcal{O}(n)$
  - 线性复杂度
  - 实际的编程问题
- 令人满意的复杂度
$\mathcal{O}(2^n)$
- 指数复杂度
- 增长过快，不可接受的
- 问题在于指数复杂度的算法显而易见，设计出多项式时间的算法极其不易
- 实例：幂集的个数$|2^s|=s^{|s|}=2^n$
  - 子集的划分是NPC问题，不存在多项式时间内回答此问题的算法

复杂度分析

学习目的：去粗存精的估算

算法分析

算法分析的任务=正确性（不变性、单调性）+复杂度

c++的基本指令等效于常数条RAM的基本指令，渐进意义下两者大体相当

主要的分析方法：

迭代：级数求和
递归：递归跟踪+递推方程
猜测+验证

级数

算数级数：与末阶平方同阶
幂方级数：比幂次高一阶
几何级数：与末项同阶
收敛级数：$\mathcal{O}(1)$
调和级数：$\Theta(\log n)$
对数级数：$\Theta(n\log n)$

利用二维图形理解复杂度，面积即是需要执行的时间

虽然面积减少了，但是根据复杂度是相同的

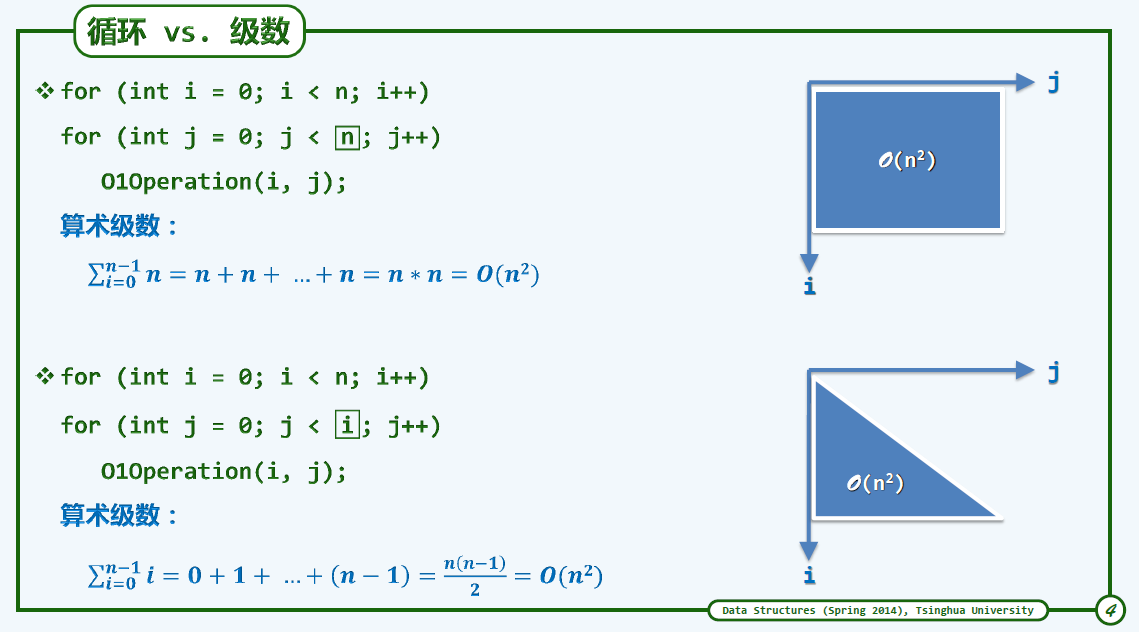
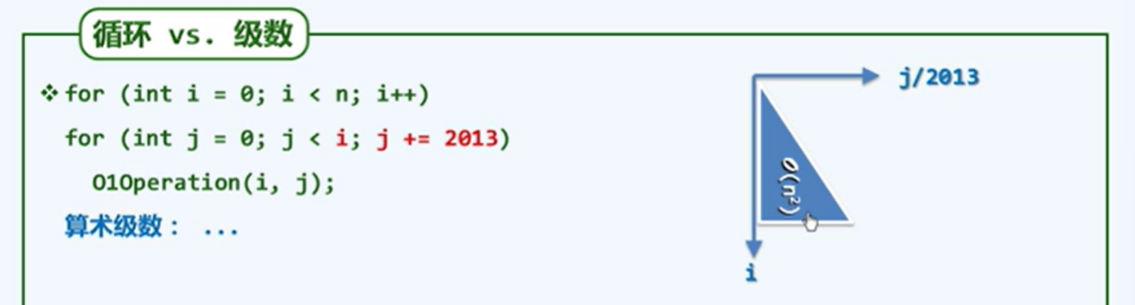
实例：Bubble Sort

消除相邻逆序元素

void bubble_sort(int A[],int n){
    for(bool sorted=false;sorted=!sorted;n--){
        for(int i=0;i<n-1;i++){
            if(A[i]>A[i+1]){
                swap(A[i],A[i-1]);
                sorted=false;
            }
        }
    }
}

接下来证明算法的正确性中止复杂度

不变性：当经过$k$轮扫描后，最大的$k$个元素必然已经出现在集合最后
单调性：当经过$k$轮扫描后，问题的规模缩减至$n-k$
正确性：经过至多$n$次扫描后，算法必然中止且能给出正确解答

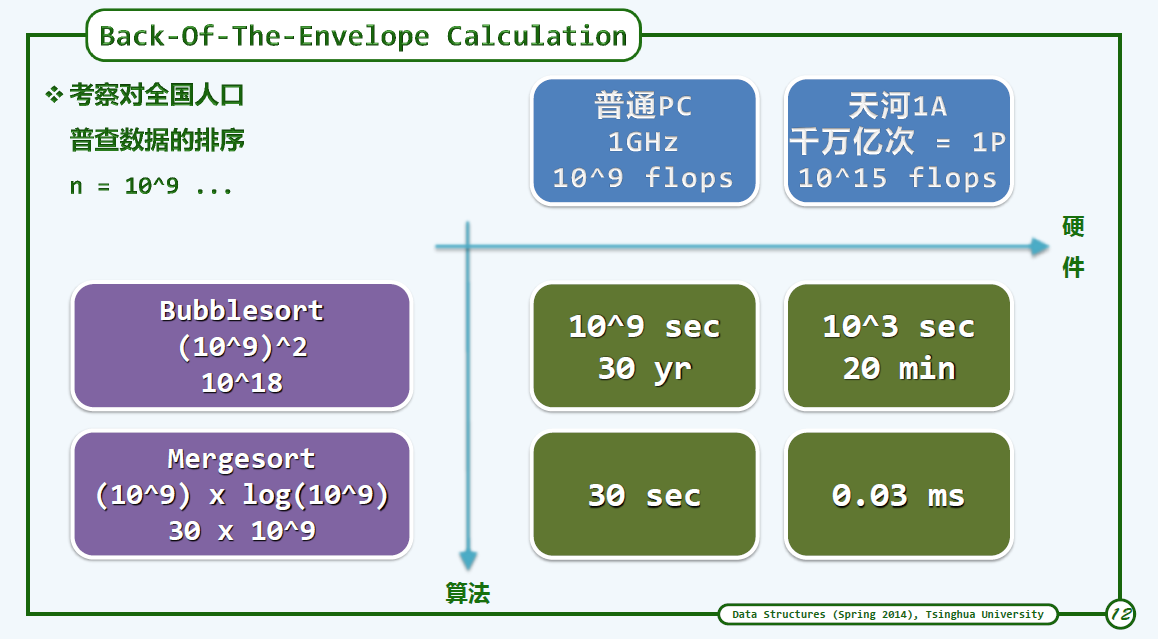
封底运算

Back of the envelope calculation

1天=$10^5$秒

1生=1世纪=$3\times10^9$秒

三生三世=$10^{10}$秒

CPU 1GHZ 每秒进行的运算$10^9$

迭代与递归

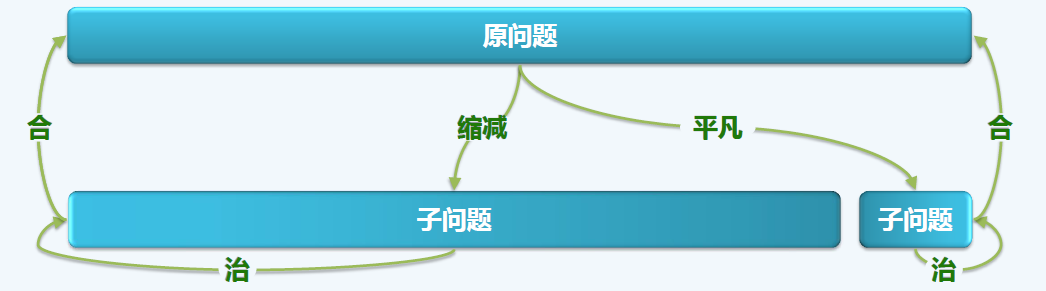
核心思想：削减问题有效规模

为求解一个大规模的问题，可以将其划分为两个子问题：

一个平凡
另一个规模递减

分别求解子问题，由子问题的解得到原问题的解

1
2
3

int sum(A[],n){
	return (n<1)?0:sum(A,n-1)+A[n-1];
}

累积所需递归实例所需的时间即可获得算法执行时间

Alleysira's blog

Algorithm and Data Structure

第一章：绪论

计算

算法

好的算法

计算模型

算法分析

理想模型

图灵机模型

RAM

渐进复杂度

大$O$记号

大$\Omega$记号

复杂度分析

算法分析

级数

实例：Bubble Sort

封底运算

迭代与递归