Notes on CCS 17 Practical Secure Aggregation for Privacy-Preserving Machine Learning
学习论文(https://eprint.iacr.org/2017/281.pdf)
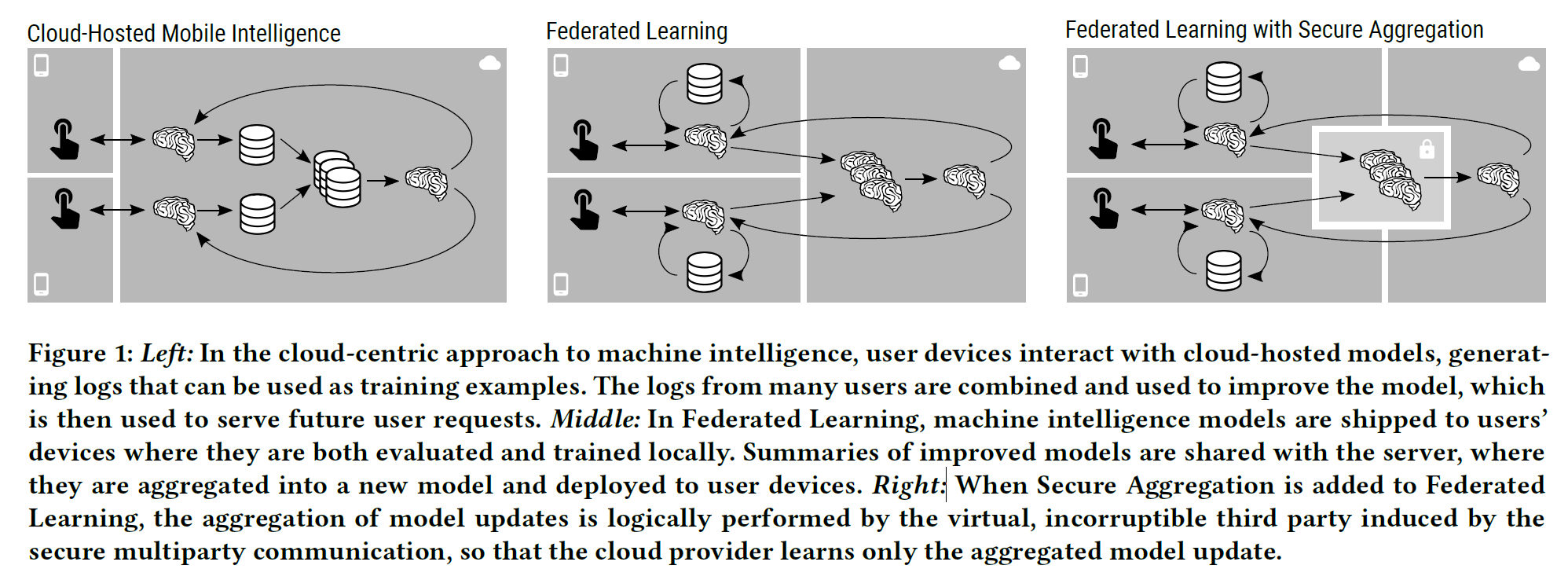
安全模型
- honest-but-curious
- active adversary
Secure aggregation for federated learning
利用用户的输入习惯训练神经网络,预测用户下一个可能输入的词
用户上传的参数是基于私人数据库的高维向量
使用mini-batch随机梯度下降算法
考虑中央服务器可能会观察某个用户多次上传的参数来学习该用户最常输入的词汇;实际上服务器只需要获得全体用户的子集的向量的加权平均即可
采用安全聚合协议能够保证服务器只可能学习到随机选取的子集用户群体的特征,但无法确定是哪一个用户
挑战
- 移动设备可能随时掉线,需要保证协议的鲁棒性
- 由于上传的参数可能比较大,对流量计费的用户来说是额外负担
- 移动设备无法直接与其他移动设备建立通信信道(通常需要服务器)
安全聚合协议的需求:
- 在高维数据上运行
- 通信效率高,甚至包括对于每个实例上新的一群用户的情况
- 对用户掉线鲁棒
- 在服务器协调有限、无认证的网络中的提供尽可能强的安全性
Cryptographic primitives
Secret sharing
本文采用Shamir的秘密分享方案
参数
有限域$\mathbb{F}=\mathbb{Z}_p,p$是公开的大素数,有限域的大小$l>2^k$,$k$是方案的安全参数(由于协议需要秘密分享参与者的私钥)
秘密分享算法
$SS.share(s,t,\mathcal{U})\to \{(u,s_u)\}_{(u\in\mathcal{U})}$
$\mathcal{U}$是$n$个用户ID的集合,$t$是门限,满足$|t|\leq \mathcal{U}$。算法输出秘密碎片和用户id对的集合
秘密重构算法
$SS.recon(\{(u,s_u)\}_{u\in \mathcal{U}},t)\to s$
需要保证此时输入的秘密碎片和用户id对的集合$\mathcal{|V|}\geq t$
正确性
如果
满足
即不同的密文产生的碎片是同分布的
Key agreement
密钥协商协议包括3个算法$(KA.param,KA.gen,KA.agree)$,具体采用了DH密钥协商协议和哈希函数
$KA.param()$产生公开参数,$KA.gen()$允许用户生成公私钥对,$KA.agree()$允许用户采用自己的私钥和另一用户的公钥协商一个新的密钥
- $KA.param(k)\to (\mathbb{G^{‘}},g,q,H)$
- $KA.gen(\mathbb{G^{‘}},g,q,H)\to(x,g^x),x \in \mathbb{Z}_q$
- $KA.aggree(x_u,g^{x_v})\to s_{u,v}=H(g^{x_ux_v})$
面对honest-but-curious的敌手,安全性参考DDH假设

考虑active adversary,敌手可以获得任意$s_u^{PK},s_v^{PK},KA.agree(s_u^{SK},s^{PK}),KA.agree(s_v^{SK},s^{PK})$,仍然无法分辨$s_{u,v}$和随机串($s^{PK}$显然不能是$u/v$的)

Authenticated Encryption
参考Introduction to Modern Cryptography中的定义,满足CCA安全和不可伪造
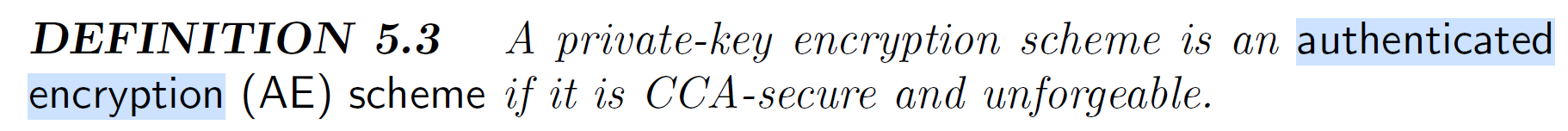

不可伪造的非形式化理解是敌手可以任意查询带有正确密钥的加密算法Oracle,最后输出密文,满足密文正确解密且不在之前查询的序列中
CCA安全的非形式化理解是敌手可以查询加解密Oracle,自行生成2个明文无法区分加密结果


提供保密性和完整性
包括三个算法:$Key.gen(),AE.enc(),AE.dec()$
满足IND-CPA与IND-CTXT
考虑使用MAC和symmetric encryption认证加密的三种实现方式:
加密和MAC同时执行:$c\gets Enc_{k_E}(m),t\gets MAC_{K_M}(m)$
先加密再MAC:$c\gets Enc_{k_E}(m),t\gets MAC_{K_M}(c)$
- 先MAC再加密:$t\gets MAC_{K_M}(m),c\gets Enc_{k_E}(m|t)$
PRG
保证接受定长的种子,输出和输出空间内随机均匀取值计算上不可区分
Signature Scheme
UF-CMA secure signature scheme
包括三个算法$(SIG.gen,SIG.sign,SIG.ver)$
PKI
防止服务器模拟任意的数量的客户端,需要引入PKI使得客户端注册身份,注册得到$(u,d_u^{PK})$
Technical Intuition
协议的目标:server只能得到来自大部分用户的$\sum_{u\in \mathcal{U}}x_u$,用户无法得知任何其他人的信息
Masking with One-Time Pads.
aggregato# r计算并发送$y_u$
server计算
存在的问题是用户必须交换$s_{u,v}$即与其他用户协商的密钥,带来的通信开销是$|\mathcal{U}|\times|x|$;以及用户不能离线
Efficient Communication and Handling Dropped Users
- 优化通信开销——令$s_{u,v}$为伪随机数生成器的输出,只需要约定种子即可
- 解决离线问题,最朴素的做法是要求其余在线用户上传和离线用户协商的种子。如此做可能带来大的通信开销以及可能存在在线用户也掉线的情况,轮数可能等于用户个数$n$
- 采用门限秘密分享来解决这个问题,但可能用户的隐私信息可能会被服务器恢复,即$y_u-恢复的值$。恶意的敌手可以通过宣称用户掉线来获得该用户的隐私
Double-Masking to Protect Security
- 通过添加新的值$b_u$来防御中心服务器不可信的情况,同样采用秘密分享分享出去
- 服务器对于每个用户$u$,必须选择向在线用户$v$请求$b_u$碎片还是$s_{u,v}$碎片;
- 诚实的用户$v$不会同时泄露同一个用户的两个碎片
Putting it all Together
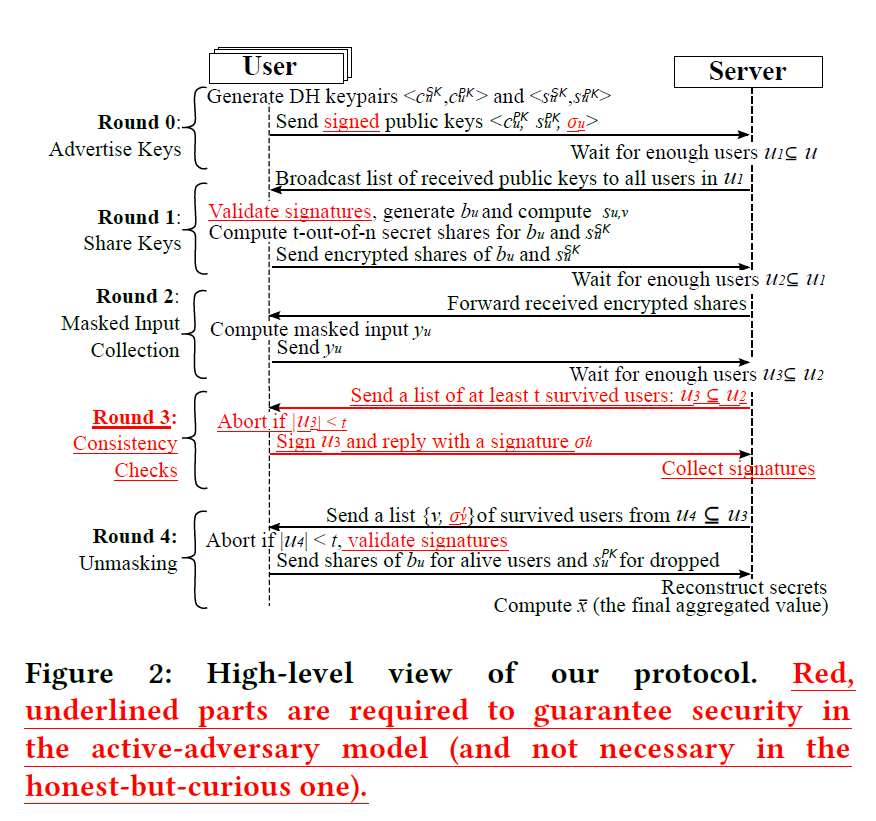
A Practical Secure Aggregation Protocol
Set up

此处标记的算法应该是$KA.para(k)$
考虑参与的用户列表
- $\mathcal{U_1}$是指正确生成了两对公私钥并发送给服务器的用户,$\mathcal{U_1} \subseteq \mathcal{U}$
- $\mathcal{U_2}$是指收到了服务器下发的用户公私钥集合,生成了自己的$b_u$并将$b_u \ s_u^{SK}$进行了秘密分享,与另一用户进行密钥协商并认证加密两者之间的对应关系和两个秘密分享的碎片,上传密文之后的用户 $\mathcal{U_2} \subseteq \mathcal{U_1}$
- $\mathcal{U_3}$是指协商$s_{u,v}$计算并加密上传了自己的参数之后的用户 $\mathcal{U_3} \subseteq \mathcal{U_2}$
- $\mathcal{U_4}$指的是上传之后掉线的用户,该用户的$s_{u,v}$已经被计算在结果中需要减去;$\mathcal{U_4} \subseteq \mathcal{U_3}$(方便理解,与原文记号不同)
- $\mathcal{U_5}$是指未掉线的用户(与原文记号不同)
Advertise keys
每个用户生成两对公私钥,$c$用于进行密钥协商作为认证加密的密钥;$s$进行密钥协商后作为伪随机数生成器的种子

Share Keys
$e_{u,v}$采用用户$u,v$协商的密钥加密了用户间的对应关系以及$u\to v$的私钥碎片和$b_u$的碎片,服务器无法解密

MaskedInput Collection
用户之间协商出PRG的种子$s_{u,v}$之后,在本地计算$y_u\gets x_u+PRG(b_u)+\sum_{v\in\mathcal{U_2}}P_{u,v}$并发送

Unmasking
服务器进行求和,由于服务器维护参与者的集合,能够发现用户掉线。对于掉线的用户,重构$s_u^{SK}$来计算需要加上的值

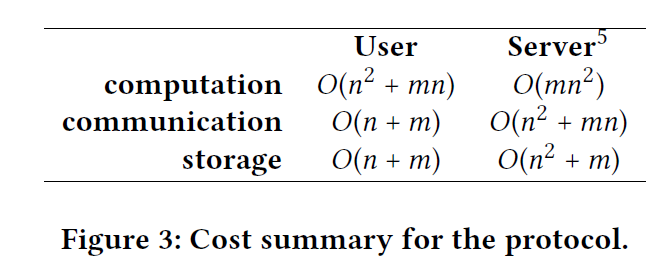
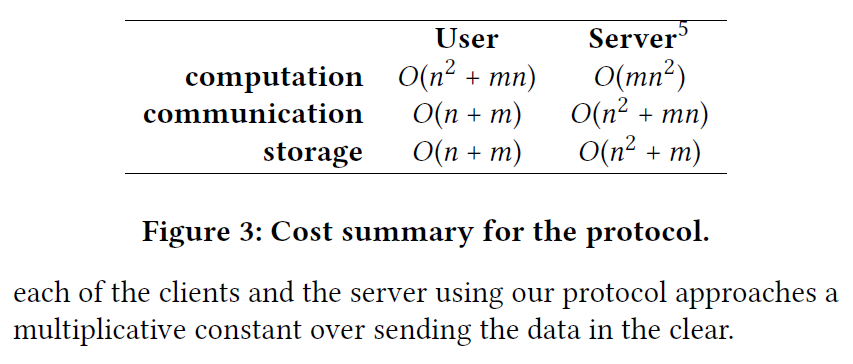
Performance analysis
考虑单一服务器和$n$个用户的情况,用户数据的维度为$m$
Related work
基于MPC的方案
基于混淆电路的MPC适用于2-3个参与者
基于秘密分享的MPC可以扩展到数百规模的用户
- 通信开销比较高
基于Dining Cryptographers Networks
- 有待学习
基于门限同态加密的方案
- 计算昂贵/需要额外的安全假设