Alleysira's blog
0%

Security proof

Posted on Edited on In

密码学安全归约技术：壬寅年的见解

学习郭福春老师面向西电的安全规约分享录屏： https://www.bilibili.com/video/BV1AY4y1n775?share_source=copy_web&vd_source=4487439a1220fa77bb4a6f0079c98794

Outputs Force Inputs.

image-20221019170832942

小白成长路线

密码学对安全的定义

PPT的敌手只能以可忽略的概率解决问题

计算安全：随着时间投入增加，解决问题的概率增加（公钥密码常用的概念）

信息论安全：one-time pad（无法实际使用）

安全规约

  • 假设存在PPT敌手能够在安全模型下攻破方案
  • 构造一个中间方案，面对已知的困难问题，敌手可以攻破该困难问题
  • 困难问题确实是困难的，假设错误

规约基础问题

simulated game和proposed game之间需要满足不可区分，两者的区别在于敌手同时得到了两个公钥，而不是有先后顺序

image-20221019171830985

image-20221019172439903

abort和不可区分：敌手是一个算法，没有记忆，可以重新初始化

小专如何看看待研究问题和研究内容

image-20221019174231071

image-20221019174507793

image-20221019174756033image-20221019174756092

安全规约相关的研究内容

安全规约究竟好不好

考虑以下4部分

  • security model
  • proof model
  • reduction cost
  • strong/week assumption

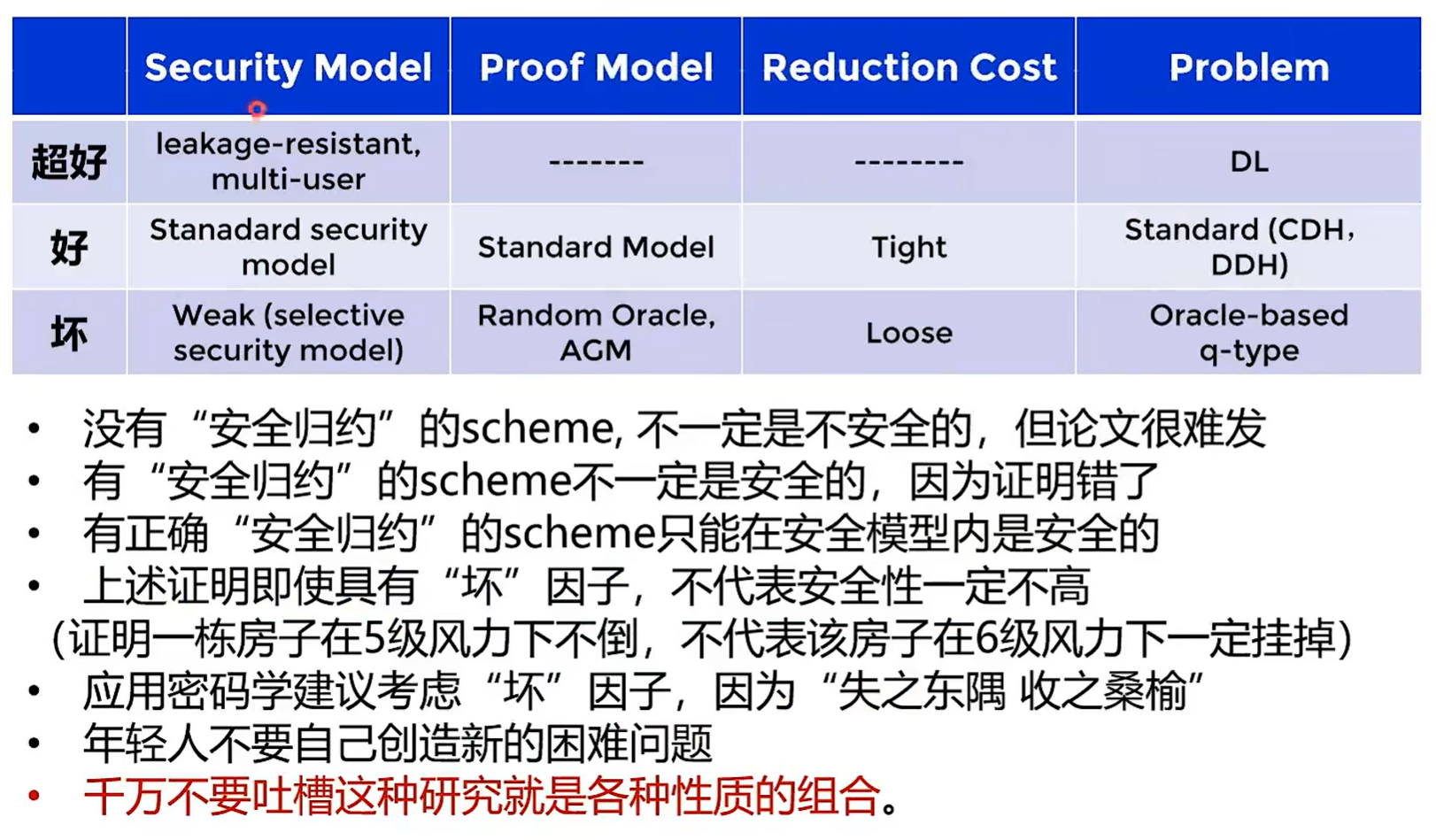
image-20221019175153652

（之前的签名论文就是q type）

有安全证明的方案只在安全模型内安全

安全规约和其他证明的区别

  • game-based proof
  • simulation-based proof

image-20221019175859049

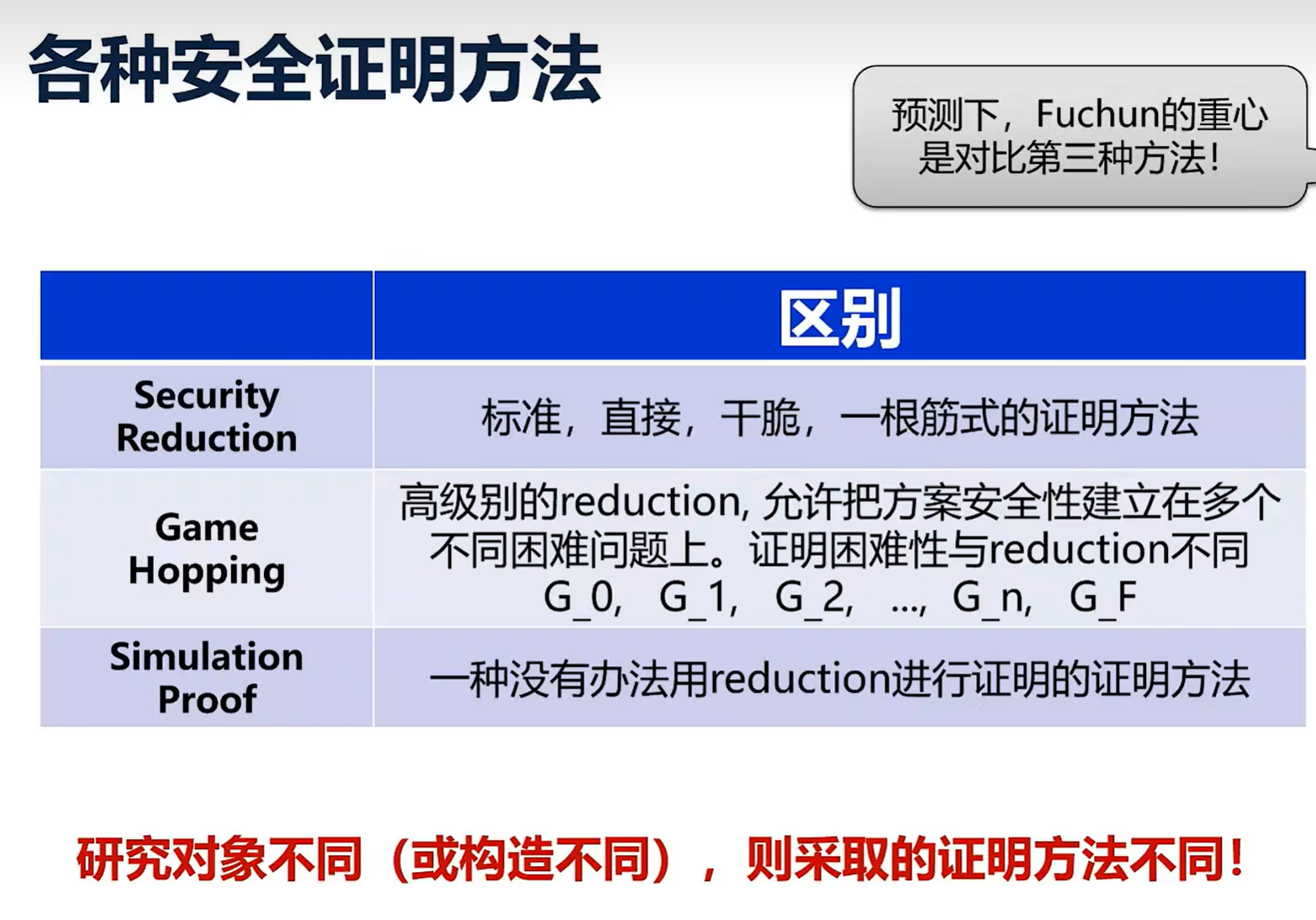
image-20221019175948438

game hopping类似于Hybrid

image-20221019180319854

清楚定义了敌手会输出什么，能够知晓哪些信息

image-20221019180355680

敌手没有特定的输出

image-20221019180616201

image-20221019180653862

image-20221019180908743

Random oracle

Overview

An idealized model ，尚无人证明random oracle存在，但可以使用可信方的形式来实现

假设存在一个完全随机、公开可访问的哈希函数，只能通过查询oracle来取值

可采用以下形式化的方法来设计密码方案：

  • 假设世界上存在random oracle，并且方案在random oracle模型下可证明安全
  • 需要在现实世界中实现方案时，采用一个恰当设计的密码学哈希函数$H(x)$即可，即当需要查询random oracle时，计算$H(x)$

以上的设计需要实际上使用的密码学哈希函数能够足够好地模拟random oracle，所以第一步的证明在现实世界中是安全的。问题在于没有理论证明以上的模拟是足够好的，具体的哈希函数代码实现也不能与随机函数的行为一致

random oracle下的证明实际是在证明方案没有固有的设计缺陷，并没有证明任何实际的方案实现是安全的

Details

将random oracle理解为一个黑盒，接收输入为比特串，输出为比特串，内部的工作机理是未知且不可构造的，任何参与者（包括敌手）可以和黑盒交互；查询是隐私的，其他人无法观察参与者的输入$x$，甚至无法得知某个参与者是否查询过（合理性在于，参考本地调用哈希函数）

黑盒具有一致性，对于同一输入的输出保证不发生变化

如何构造$H$,考虑一个初始为空的$(x_i,y_i)$表，对于输入$x\neq x_i \in box$，随机选择$y\in \{0,1\}^l$并存入表内即可；如果输入$x = x_i \in box$，则输出对应的$y_i$。显然需要提前定义输出的域

Cons

  • 存在方案在RO下安全但是使用任何现实的哈希函数时都不安全

  • 在许多现有方案中可能安全性要求过高

Pros

  • 没有已知的在RO下安全但在现实世界中受到攻击的方案
  • 如果攻击被发现了，可以更换哈希函数
  • 有证明总比没有好（摆烂.jpg）

参考 Page187 Introduction to Modern Cryptography, 3rd edition

UC安全计算

基本概念

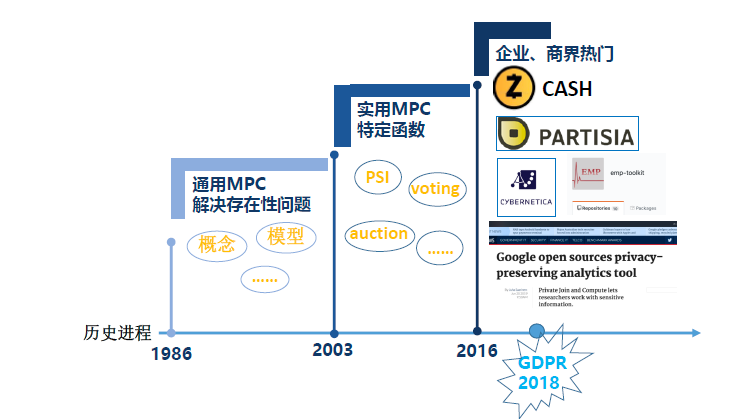
image-20230910094647770

03年之后出现了针对具体特定功能的函数

functionality的概念比函数更宽泛

image-20230910095011047

函数和功能

函数的随机性会导致结果的分布，功能就是输出为分布的函数

image-20230910095337791

考虑协议的安全性的三个维度

image-20230910095359646

  • 自适应和静态
  • 恶意和半诚实
  • PPT和计算能力无上限

MPC一般考虑蓝色的敌手

image-20230910095911654

理想现实模型

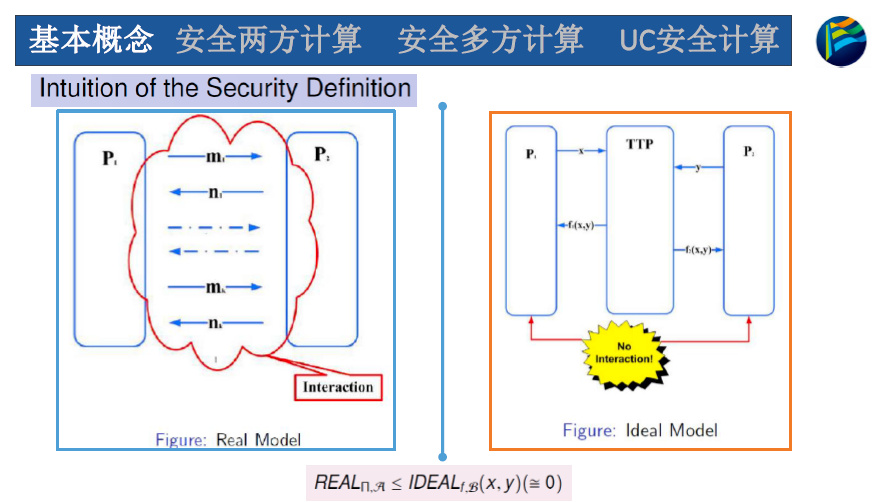
image-20230910100006539

攻击现实模型

理想模型没有信息泄露

image-20230910100728399

参与者的输出不包含在view中（可以根据输入推导出）

安全两方计算

image-20230910101050638

隐私性分f是确定性和一般情况

  • 确定性：设计两个算法$S_1,S_2$能够根据输入输出模拟出view
  • 引入随机性，多维随机变量，$S_1$需要模拟出view和output，因为随机性可能在对方输出内
    • 因为view和output具有相关性

image-20230910101429624

安全性

至少一方是诚实的

image-20230910102628943

image-20230910102720461

任意的A存在B

存在性：存在陷门置换，任何功能都能被安全计算

image-20230910103642915

以半诚实安全下OT的例子进行介绍

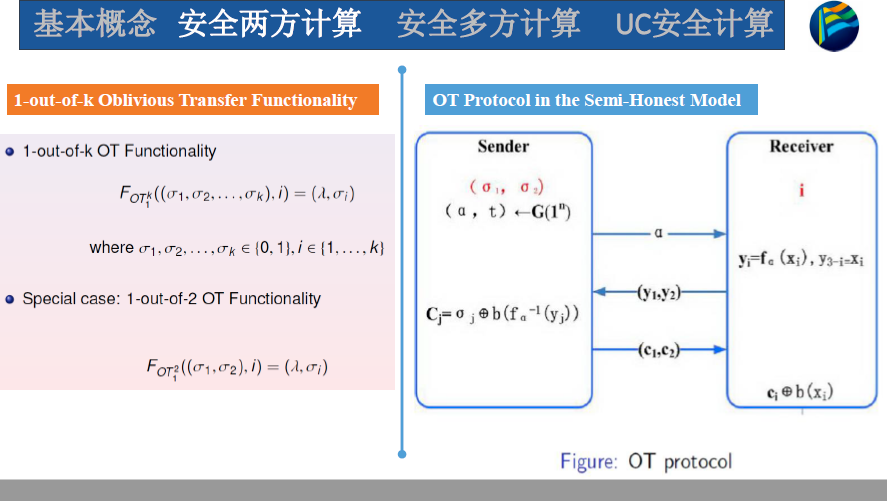
image-20230910105050387

单向置换，G是采样算法

这里利用到了hardcore predicate，参考https://zhuanlan.zhihu.com/p/588114150

image-20230910105011183

发送方 发送的时候要无差别的对$\sigma_1,\sigma_2$ 加密

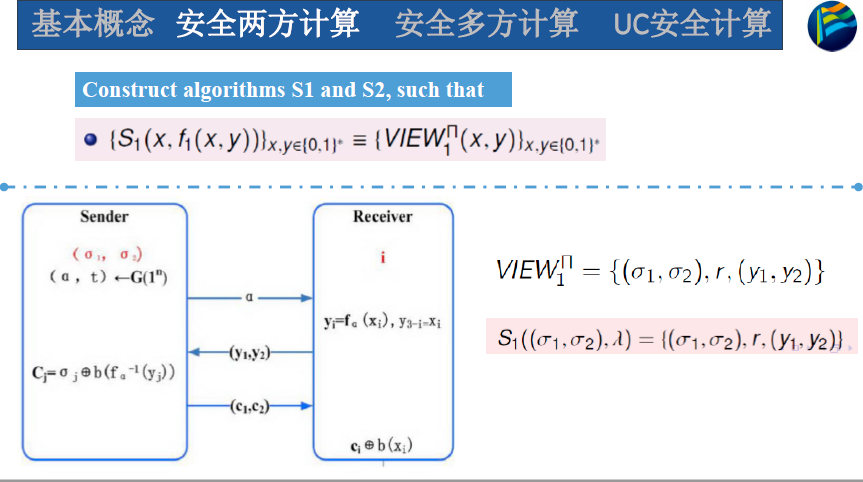
image-20230910112101925

S1只需要额外随机在定义域内选择$y_1,y_2$就可以了

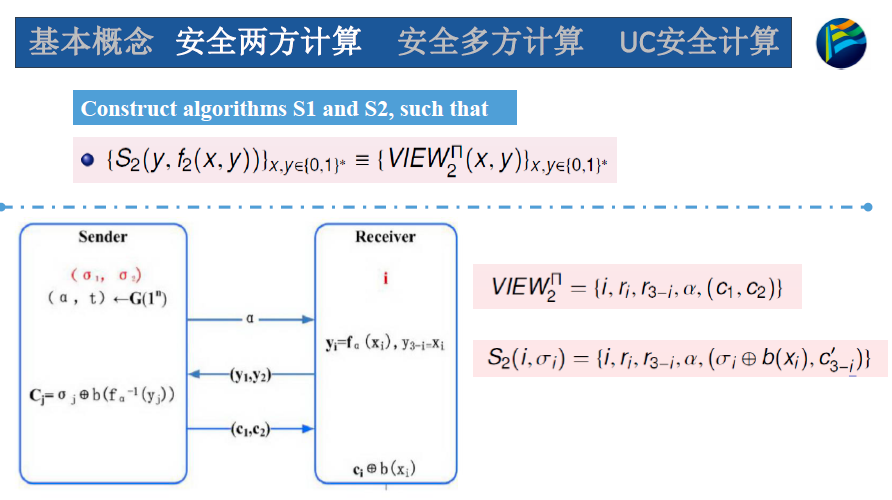
真实世界中r2和c2具有相关性，但是S2中r2和c‘2没有相关性，因此需要enhanced陷门置换

image-20230910114818996

半诚实模型的组合定理

证明了某个组件的安全性后，后续在复杂协议中利用Oracle代替组件即可

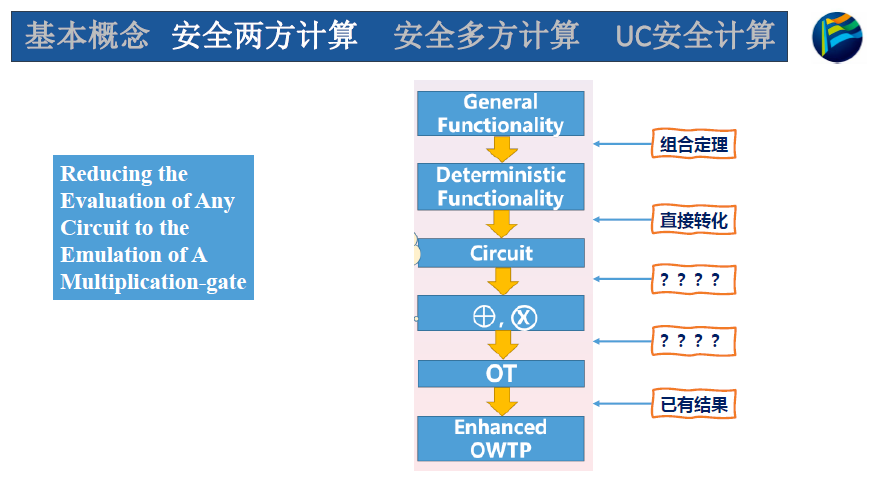
image-20230910115544604

存在性的思路

将随机性显式化，放在输入里面

电路规约为计算加法和乘法

one way trapdoor permutation

关键问题是如何能转换为计算加法和乘法的电路

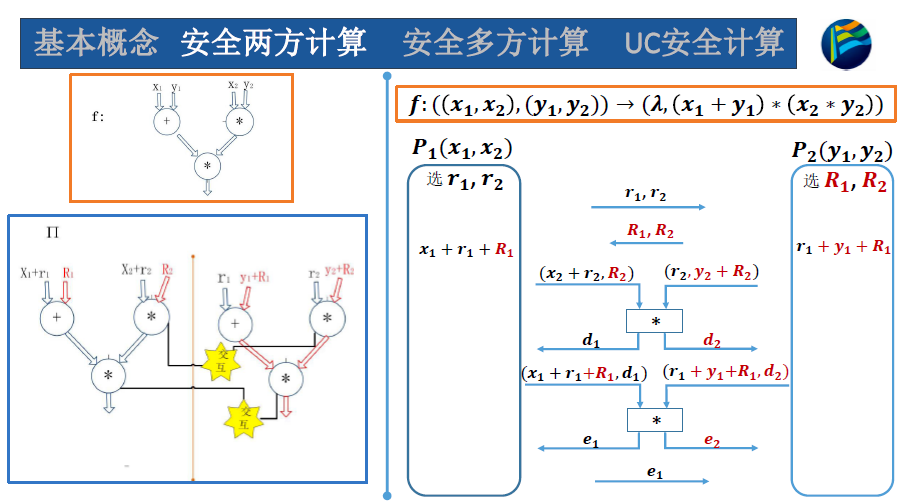
image-20230910120323000

乘法无法直接本地计算，只能交互再保证线性关系

安全多方计算

UC安全计算

引入了环境Z

  • 生成输入
  • 读输出
  • 能够自由和敌手交互

STOC01

后续应该学习这个课程 (1) UC Tutorial 1.1 - Background: Introduction - YouTube