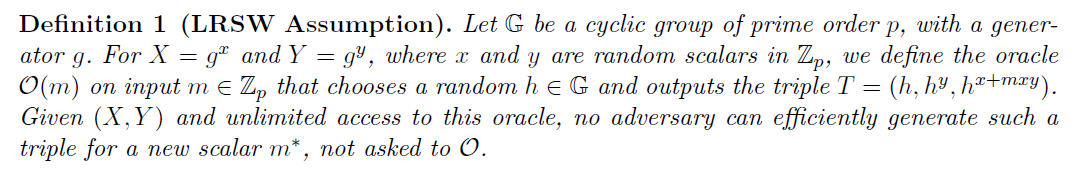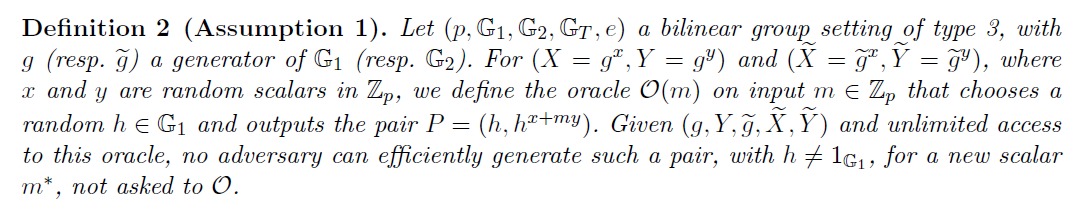Introduction

数字签名的要点在于提高效率以及适配协议（blind signature在隐私保护协议中）

Preliminaries

三个素数阶$p$的循环群$\mathbb{G_1,G_2,G}_T$之间存在如下双线性映射$e:\mathbb{G_1}\times\mathbb{G_2}\to\mathbb{G}_T$并满足三条性质：

双线性：for all $g\in\mathbb{G_1},\tilde{g}\in\mathbb{G_2}$ and $a,b\in\mathbb{Z}_p,e(g^a,\tilde{g}^b)=e(g,\tilde{g})^{a\cdot b}$
非退化性：for $g\neq 1_{\mathbb{G}_1}$ and $\tilde{g} \neq 1_{\mathbb{G}_2},e(g,\tilde{g})\neq 1_{\mathbb{G}_T}$
可计算性：for all $g\in\mathbb{G_1},\tilde{g}\in\mathbb{G_2}$存在多项式时间算法可高效计算$e(g,\tilde{g})$

[GPS08] 定义了以下三类双线性群

Type 1：$ \mathbb{G_1=G_2}$，对称双线性群
Type 2：$ \mathbb{G_1\neq G_2}$但存在efficient的同态映射$\phi:\to \mathbb{G_2} \to \mathbb{G_1}$;另一个方向不存在efficient的映射
Type 3：$ \mathbb{G_1\neq G_2}$并且任何方向都不存在高效可计算的的同态映射

Type 1正在逐渐被弃用，Type 3 具有更好的效率并和 XDH assumption 协调

一个数字签名方案由四个算法定义：

existential unforgeability under chosen message attacks

$AS.setup(k)\to pp$
$AS.keygen(pp)\to(sk,pk)$
$AS.sign(\sigma,m,sk)\to\sigma’$，其中$\sigma\gets sign((m_1,m_2,\cdots,m_n),(sk_1,sk_2,\cdots,sk_n))$此处相当于追加了一条消息再签名，且使用的私钥不能和$\{m_i\}^n$签名时使用的私钥对应
$AS.verify((m_1,m_2,\cdots,m_n),\sigma,(pk_1,pk_2,\cdots,pk_n))\to True \ or\ False$

以下是LMRS04定义的聚合签名方案

安全性类似普通签名的EUF-CMA，由如下游戏定义:

LRSW假设