Secret_sharing

秘密分享经典方案

基本定义

秘密分享的概念最早由Shamir和Blakley提出，秘密分享主要由两个算法构成：

• 分配算法：分发者将秘密$s$分割成若干个份额，在一组参与者$P=\{P_1,P_2,\cdots,P_n\}$中进行分配，是得每一个参与者都得到关于该秘密的一个份额
• 恢复算法：保证只有$P$的一部分特定的子集才能有效地恢复秘密，甚至可能得不到关于$s$的任何有用信息

(12条消息) 秘密共享(Secret Sharing,SS)_闭眼神的博客-CSDN博客

(12条消息) 【隐私计算笔谈】MPC系列专题（十五）：三方复制秘密分享_PlatON技术团队的博客-CSDN博客

Addition secret sharing

安全两方计算$a+b$，两个参与者分别持有秘密$a=a_1+a_2+a_3,b=b_1+b_2+b_3$，抗$n-1$方合谋

$server_1:c_1=a_1+b_1$

$server_2:c_2=a_2+b_2$

$server_3:c_3=a_3+b_3$

输出$c_1+c_2+c_3=a+b$

Replicated secret sharing

秘密$a=a_1+a_2+a_3$，任意两方不能合谋

$server_1:a_1,a_2,c_1=a_1+a_2$

$server_2:a_2,a_3,c_2=a_2+a_3$

$server_3:a_3,a_1,c_3=a_3+a_1$

Multiplication secret sharing

两个秘密$a=a_1+a_2+a_3，b=b_1+b_2+b_3$，分享$ab$，任意两方不能合谋（防止单点故障？）

$server_1:a_1,a_2,b_1,b_2,c_1=a_1b_1+a_1b_2+a_2b_1$

$server_2:a_2,a_3,b_2,b_3,c_2=a_2b_2+a_2b_3+a_3b_2$

$server_3:a_3,a_1,b_3,b_1,c_3=a_3b_3+a_3b_1+a_1b_3$

$c_1+c_2+c_3=ab$

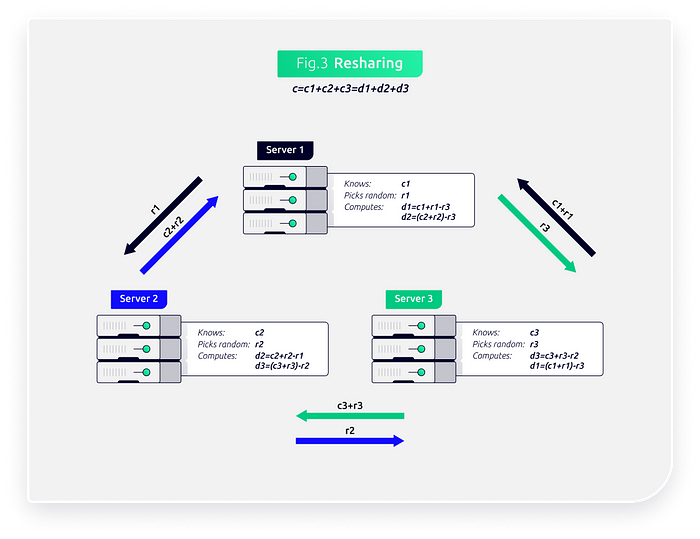
注意到此时$c_1,c_2,c_3$不再是重复秘密分享的形式（每个人有秘密的两个份额），无法继续做乘法，需要进行扩展，本地选择随机数$r_i$

$server_1 \to server_2,server_3:r_1,c_1+r_1$

$server_2 \to server_3,server_1:r_2,c_2+r_2$

$server_3 \to server_1,server_2:r_3,c_3+r_3$

$c_1’=c_1+r_1-r_3,c_2’=c_2+r_2-r_1,c_3’=c_3+r_3-r_2$

此时$server_1$知道$c_1’,c_2’$，$server_2$知道$c_2’,c_3’$，$server_3$知道$c_3’,c_1’$

门限秘密分享

如果秘密分发为$n$份且分配给一个参与者后满足：

• $n$个参与者中任何$k$个或者多于$k$个合作可以恢复秘密
• 任何少于$k$个参与者都无法获得该秘密

称以上方案为$(k,n)$秘密分享门限方案，其中$k$称为方案的门限值

如果满足任何少于$k$个参与者的子秘密都无法获得该秘密的任何信息，则称该方案是完善的(perfect)

朴素构造秘密分享方案

思想

考虑一个$n$次多项式$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0$，若有$t$对$(x_i,f(x_i))满足x_i\neq x_j,i\neq j$

$$\left( \begin{matrix} x_{0}^{n} & x_0^{n-1} & \cdots& x_0 & 1\\ x_{1}^{n} & x_1^{n-1} & \cdots& x_1 & 1\\ \vdots & \vdots & \vdots &\vdots & \vdots\\ x_{t}^{n} & x_t^{n-1} & \cdots& x_t & 1\\ \end{matrix} \right) \left( \begin{matrix} a_{n}\\ a_{n-1}\\ \vdots\\ a_0\\ \end{matrix} \right) = \left( \begin{matrix} f(x_{0})\\ f(x_{1})\\ \vdots\\ f({x_t})\\ \end{matrix} \right)$$

若设此时的秘密值为常系数$a_n,a_{n-1},\cdots,a_0$，则解线性方程组即可恢复秘密

考虑解非齐次线性方程组，由于此时等式左侧为范德蒙矩阵，

对于$n$阶的范德蒙行列式，有

$$D_n=\prod\limits_{1\leq j<i\leq n}(x_i-x_j)$$

行列式的值不为0，系数矩阵满秩，增广矩阵满秩

由于有$n+1$个未知数，需要满足$t\geq n$

构造

• 秘密分享阶段：随机选择一个$Z_q$上的$n$次多项式$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0$，并随机选取$t$个点对$(x_i,f(x_i))满足x_i\neq x_j,i\neq j,t\geq n$，将点对分发给$t$个用户，此时的门限值为$n$

• 秘密恢复阶段：任意$n$个用户或多于$n$个用户合作可以求解线性方程组恢复出常系数

Shamir门限秘密分享

Lagrange插值公式

$$f(x)=\sum\limits_{j=1}^{k}[f(i_j)\prod\limits_{l=1,l\neq j}^k \frac{x-i_l}{i_j-i_l}]\bmod q$$

满足$f(x_i)=y_i,i=1,2,\cdots,k,x_i\neq x_j$的$k-1$次多项式$f(x)=a_{k-1}x^{k-1}+a_{k-2}x^{k-2}+\cdots+a_0$是存在且唯一的

和平凡的秘密分享不同的是直接$a_0$作为秘密，只需要计算$f(0)$

利用插值公式，可以直接计算

$$f(0)=(-1)^{k-1}\sum\limits_{j=1}^{k}[f(i_j)\prod\limits_{l=1,l\neq j}^k \frac{i_l}{i_j-i_l}]\bmod q$$

基于中国剩余定理的门限方案

CRT

中国剩余定理可用于求解多个线性同余方程组

设$m_1,m_2,\cdots,m_k$是k个两两互素的自然数，令$m=m_1m_2\cdots m_k,\ m=m_iM_i,\ M_iM_i^{‘}\equiv1 \bmod m_i$

则方程组

$$\left \{ \begin{align*} x \equiv & b_1 \bmod m_1 \\ x \equiv & b_2 \bmod m_2 \\ \vdots &\\ x \equiv &b_k \bmod m_k \end{align*}\right.$$

解为

$$x\equiv M_1M_1^{'}b_1+M_2M_2^{'}b_2+\cdots+M_kM_k^{'}b_k \bmod m$$

选择参数

取$m_1<m_2<\cdots<m_n$满足

• $gcd(m_i,m_j)=1$

• $m_1m_2\cdots m_k>m_{n-k+2}\cdots m_{n-1}m_n$最小的k个数的乘积也大于最大的$k-1$个数，保证了任意的$k$个数的乘积也大于$k-1$个数的乘积

秘密分割

保证$m_{n-k+2}\cdots m_{n-1}m_n<s<m_1m_2\cdots m_k$

满足在$k-1$个数乘积和$k$个数乘积下做模运算数值不等

$s_i\equiv s \bmod m_i$

子秘密包括$\{(s_i,m_i,m)\}$

秘密恢复

任意$k$个参与者求解中国剩余定理即可

可验证的秘密分享

允许参与者验证收到份额的正确性

• 防止dealer作恶
• 防止在秘密恢复阶段上传错误份额

Feldman’s VSS

引入承诺使得参与者能够验证多项式的取值

$$v_0 v_1^i v_2^{i^2} \ldots v_t^{i^t}=g^{\sigma+a_1 i+a_2 i^2+\ldots a_t i^t} \equiv g^{f(i)}\bmod p$$

Hence $v_0 v_1^i v_2^{i^2} \ldots v_t^{i^t} \equiv g^{s_i}(\bmod p)$ if and only if $s_i \equiv f(i)\bmod q$

The Joint-Feldman DKG protocol

每个参与者在一轮中作为Dealer，其他轮作为接收者

n个参与者，每个参与者随机选择$f_i(x)=\sum_{j=0}^t a_{i,j}x^j \bmod q,f_i(0)=a_{i,0}=secret$

$pk=g^{\sum^t_1 a_{i,0}},sk=\sum^t_1 a_{i,0}$

每个参与者的私钥份额为$sk_j=\sum f_i(j)$

公开验证参数 $A_k=g^{\sum a_{i,k}}$

恢复秘密

定义$h(x)=\sum f_i(x),sk_j=h(j)$，$h(x)$极大概率是t阶多项式，因此需要t+1个份额即可恢复h(x)

验证份额正确性

$$\begin{aligned} A_1^{j^1} \cdots A_t^{j^t} & \equiv\left(g^{a_{11}} \cdots g^{a_{r 1}}\right)^j \cdots\left(g^{a_{1 t}} \cdots g^{a_{r t}}\right)^{j^t} \\ & \equiv g^{\sum_{k=0}^t \sum_{\ell=1}^r a_{\ell k} j^k} \\ & \equiv g^{\sum_{\ell=1}^r \sum_{k=0}^t a_{\ell k} j^k} \\ & \equiv g^{\sum_{\ell=1}^r\left(a_{0 k}+a_{1 k} j+\ldots+a_{t k} j^t\right)} \\ & \equiv g^{\sum_{\ell=1}^r f_{\ell}(j)} \equiv g^{s k_j}(\bmod p) . \end{aligned}$$

Gennaro et al. (2006) 指出了这种构造不安全，敌手可以多次利用投诉机制来控制公钥的最后一个比特，因此JF DKG不能用做安全的DKG方案