Jia M, Chen J, He K, et al. Redactable Blockchain From Decentralized Chameleon Hash Functions[J]. IEEE Transactions on Information Forensics and Security, 2022, 17: 2771-2783.
去中心化变色龙哈希函数的构造
包含五个算法:
$Key\ generation$ 密钥生成算法:需要$t$个参与者$\{P_1,\dots,P_t\}$在线合作共同生成密钥,$g$是循环群生成元,参与者$P_i$ 如下执行
随机生成$t-1$阶多项式:$f_i(x)=\sum_{j=0}^{t-1}a_{i,j}x^j$,秘密为常数项$f_i(0)$
给参与者$P_j$发送$f_i(ID(P_j)),(g^{f_i(ID(P_1))},\dots,g^{f_i(ID(P_t))}),g^{f_i(0)}$,类似于拉格朗日插值法,把秘密放在了幂指数上
- $f_i(x)$是否有必要放在幂指数上?如果不放在指数上任何参与者都可以拿到输出私钥的值了
- $f_i(ID(P_j))$的意义在于构建系统的私钥,由于私钥是$s_i=\sum^t_{j=1}f_j(ID(P_i))$,需要其他人的多项式在自己身份处的取值
参与者$P_i$收到参与者$P_j$发送的$f_j(ID(P_i)),(g^{f_j(ID(P_1))},\dots,g^{f_j(ID(P_t))}),g^{f_j(0)}$后,计算拉格朗日插值判断是否正确,即计算是否成立
输出公钥$g^s=\prod_{j=1}^t f_j(0),s=\sum^t_{j=1}a_{j,0}$,相当于$t$个参与者每个人私钥的和,但任何参与者都无法计算出公钥的$s$;输出私钥$s_i=\sum^t_{j=1}f_j(ID(P_i))$,私钥可以用来恢复公钥
- 公私钥生成体现了公平性,$t$个参与者
- 考虑敌手$P_j$偷听,尝试恢复$P_i$的私钥$s_i=\sum^t_{k=1}f_i(ID(P_k))$缺一个份额$f_i(ID(P_i)$,以下秘密分享同理,缺少对自己的取值
- 密钥生成阶段通信复杂度为$O(t^2)$
$Hashing$ 哈希算法:输入公钥$g^s$,任意长度消息m,先计算$\mu\gets H(g^s,m)$,$H$是密码学哈希函数,满足$H:\mathbb{G} \times \{0,1\}^{\star} \to \mathbb{G} $,随机选择$e\in \mathbb{Z}_p^*$,输出随机数$r=(g^e,g^{se})$,输出哈希$h=g^e\mu^m$
- 此处的$H$选择会影响安全性
- 哈希算法里用到了两次m,密码学哈希函数的输入m相当于提供随机性,$\mu^m$保证难以寻找碰撞,m在外面方便计算,实际上并不是想要修改的内容,用的是$header$
$Rehashing$算法:给定公钥$g^s$和原始的消息-随机数对$(m,r=g^e,g^{se})$,计算哈希$h\gets g^e\mu^m$并输出
$Adaptation$算法:输入私钥份额$s_i$,原始的消息-随机数对$(m,r=g^e,g^{se})$,新的消息$m’\in\{0,1\}^\star$,参与者$P_i,i\in[t]$如下执行:
计算$g^{e’}\gets g^e\mu ^{m-m’}$
计算$\eta_i\gets(g^{e’})^{\lambda_i \cdot s_i },\lambda_i=\prod^t_{l=1,l\neq i}\frac{ID(P_l)}{ID(P_l)-ID(P_i)}$,把$\eta_i$发送给参与者$P_j,j\in[t],j\neq i$
参与者$P_i$收到$\eta_1,\dots,\eta_{i-1},\eta_{i+1},\dots,\eta_{t}$后,计算$g^{se’}\gets\prod^t_{j=1}\eta_j$,输出更新后的随机数$r’=(g^{e’},g^{se’})$
其实就是用$t$个私钥恢复出公钥的指数
通信复杂度为$O(t^2)$
$Verification$:输入公钥$g^s$和原始的消息-随机数对$(m,r=g^e,g^{se})$以及修改后的消息-随机数对$(m’,r’=g^{e’},g^{se’})$,如果计算的哈希值$g^e\mu^m=g^{e’}\mu^{m’}$相等且$(g,g^s,g^{e’},g^{se’})$是DH组,输出1,否则输出0
密钥更新阶段
目的:节点可能动态加入或离开,敌手可能掌握超过$t$个份额,需要在不改变秘密的情况下扩大门限到$t’$
目前已经有n个节点掌握多项式$F(ID(i),y)$,需要$t$个份额就能恢复秘密
全节点$\{P_i,\dots,P_{2t’}\}$执行$Zero(\{F(ID(P_i),y),t’-1\}^{t})$
随机选择$(t’-1,2t’-1)$阶多项式$R(x,y)$,满足$R(0,0)=0$
$\{F(x,ID(i))\}^{2t’} \gets Handout\{F(ID(i),y)\}^t$
$\{R(ID(i),y)\}^{2t’}\gets Transform\{R_i(x,ID(i))\}^{2t’},R_i(x,ID(i)$是$t’-1$阶
$\{R(x,ID(i))\}^{2t’} \gets Handout\{R(ID(i),y)\}^{2t’}$
实现了对份额的更新,新的$t’-1$阶多项式满足$F’(x,ID(P_i))=F(x,ID(P_i))+R(x,ID(i))$
现在分发给$n’$即可,执行$\{F’(ID(i),y\}^{n’} \gets Handout\{F’(x,ID(i))\}^{2t’}$
- $F’(x,y)=F(x,y)+R(x,y),F’(0,0)=F(0,0)=s$
- 更新份额相较于重新生成私钥再分配的区别在于,省去了执行$DCH.KeyGen()$的时间
RSA累加器
主要参考知乎这篇文章理解,本文写的不够清楚
- acc字段存当前RSA累加器的值,RSA累加器把所有区块的$last_hash$编码进去,同一高度的区块acc值一样
- 当区块2内的编辑请求$tx_{req1}$修改$tx1$为$tx1’$后,生成区块3,区块2内的acc值更新
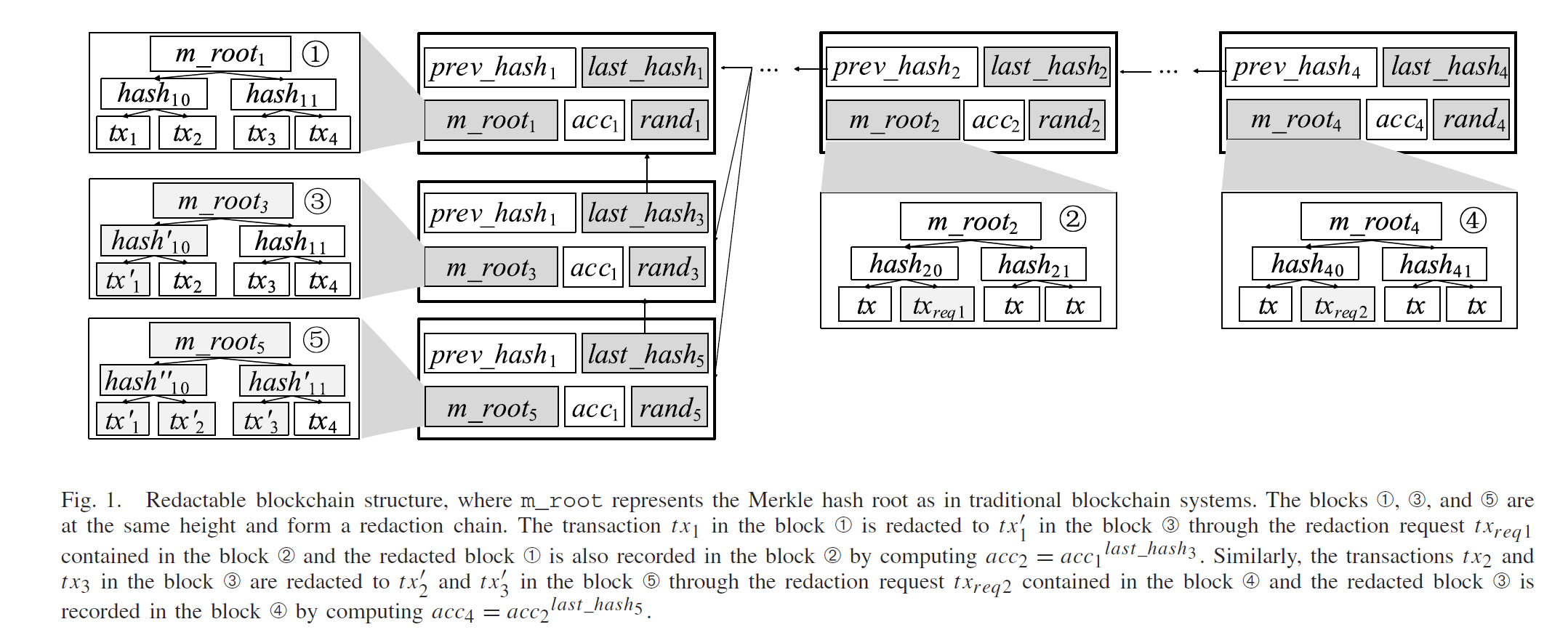
一致性检查
编辑会导致同一区块高度可能存在不同的区块,客户端需要检查是否区块被编辑过
- 客户端发送想要查询的区块$header,hash(header)$给任意节点,节点本地查询RSA累加器
- 节点收到成员证明或者非成员证明后验证即可
安全性分析
Decentralization
如果敌手试图通过$(m,r=g^e,g^{se})$来恢复$s$实现高效寻找碰撞,考虑到在系统稳定时,密钥作为常数项
$F(x,0)=s+\sum_{i=1}^{t-1}a_ix^i$被分享给$n$个节点,节点拥有份额$(IP(P_i),F(IP(P_i),0))$,超过$t$个节点同意即可恢复私钥。由于敌手只能控制$t-1$个节点,无法恢复私钥
在私钥更新阶段,每个节点最多同时掌握$2t-1$阶多项式$F(i,y)$和$t-1$阶$F(x,i)$,节点能够获得$t-1$阶多项式
敌手最多获得$t-1$份$F(x,0)$和$F’(x,0)$,无法恢复私钥
Traceability
考虑到同一高度所有被编辑的区块组成一条编辑链,所有编辑可以被高效审计(RSA累加器的必要性体现在一致性检查)
问题
- 提到新的创世区块,应该是是自己新建一条链,如何集成到现有的区块链系统中
- 最初$t$个掌握变色龙哈希函数私钥的节点怎么选,安全性
- 直接用节点身份的哈希值,属于半中心化信标
- 在包含修改请求的交易上链后,其他区块链上的节点如何修改$header \to header’$
- 修改区块头的结构后,增加的3个字段会带来额外的存储开销
- RSA累加器的必要性在哪里
- 将编辑后的区块加入到RSA累加器中
- 每次生成新的区块,节点本地更新RSA累加器的值
- 节点验证区块的有效性时想要知道该区块是否被编辑过
- 如果不是使用RSA累加器,其他方案如何解决区块的区分问题
- RSA累加器的值能保证同步吗?可能存在某个恶意节点的未即时更新acc,客户端向恶意节点查询本已经被修改过的区块,该恶意节点返回该区块未被编辑。如果不同步,下一次生成区块的acc计算会错误;如果编辑对自己不利,可能在出块时才更新acc
- [LMW+23]提到了扩展头部的作用是保证类似的本地数据结构的同步
- 初始化的RSA的$N$和$g_1$也需要分布式生成,论文给了参考的算法,没有仔细了解
需要的映射哈希函数,将$x$映射为素数$SH(x)$,这种映射怎么找
- github的RSA accumulator已找到
last_hash字段是新产生区块更新后的头部的哈希,如果是对之前区块的编辑,$last_hash$是该区块的头部哈希,不是编辑的区块是否该字段为空?
- 每次秘密分享都是可验证的,不是公开可验证
- 如果将RSA累加器替换为bloom filter?
- 思考可行性:布隆过滤器提供高效的成员证明,非成员证明很可能不出错
- 如何保证参与者的bloom filter一致,区块头加上布隆过滤器的哈希值?类似于RSA的acc
- https://zhuanlan.zhihu.com/p/601973839