LMW23

Li J, Ma H, Wang J, et al. Wolverine: A Scalable and Transaction-Consistent Redactable Permissionless Blockchain[J]. IEEE Transactions on Information Forensics and Security, 2023.

Introduction

区块链中有两种链接关系：hash链接和签名链接

• 哈希链接存在于不同区块的区块头之间
• 签名链接存在于不同区块的区块体的交易之间，签名链接是满足了之前交易的challenge script的见证

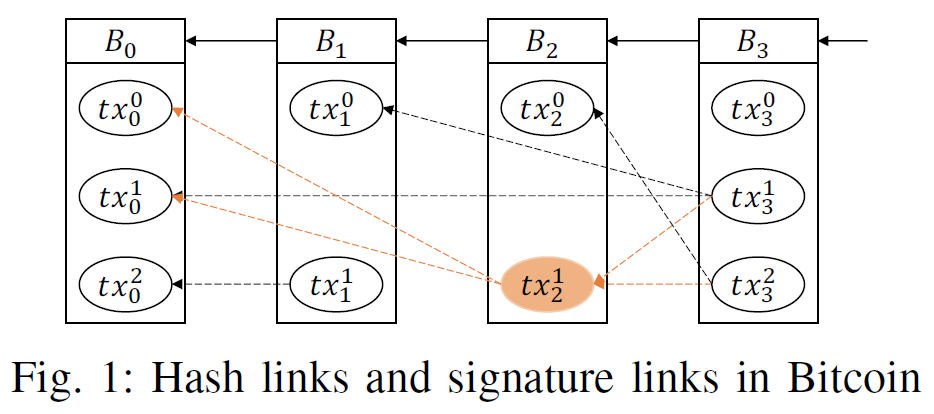
考虑删除区块$B_2$内的交易$tx^1_2$，可能导致四条交易链接失效$tx^0_0\gets tx^1_2,tx_0^1\gets tx^1_2,tx^1_2\gets tx_3^1 ,tx^1_2\gets tx_3^2 $

其中交易$tx^0_0\gets tx^1_2,tx_0^1\gets tx^1_2$可能被双花

交易$tx^1_2\gets tx_3^1 ,tx^1_2\gets tx_3^2$可能会失效

Related work

[DMT19]为了实现追责，扩展了区块头增加了$old_merkle_root$字段，Reparo相当于将这个字段单独存储在数据库中而不修改区块结构，存在投票周期长和$n=3f+1$；这两篇文章都考虑+了交易的一致性问题，因此将编辑操作限制在非金融字段，不适用于UTXO

Preliminary

DRB

对于参与者$\{P_1,\dots,P_n\}$，$(t,n)$去中心化随机信标包含如下算法：

• $Setup(1^\lambda)\to pp$
• $CmteGen(pp,t,n)\to(cpk,sk_1,\dots,sk_n)$:交互式协议，输出委员会的公钥和参与方对应的私钥
• $PartialRand(cpk,sk_i,st_{l-1})\to s_i$：输入$l-1$轮状态$st_{l-1}$，计算部分值$\sigma_{l,i}$和对应的证明$\pi_{l,i}$，并且$s_i=(i,\sigma_{l,i},\pi_{l,i})$
• $CombRand(cpk,st_{l-1},\varepsilon)\to (\sigma_l,\pi_l)$：输入$\varepsilon=\{s_i\}_{i\in I},|I|\geq t+1$
• $VerifyRand(cpk,st_{l-1},\sigma_l,\pi_l)\to d\in\{0,1\}$
• $UpdState(cpk,st_{l-1},\sigma_l,\pi_l)\to st_l$：输入上一轮的状态，输出更新后的当前轮的状态

Overview

System model

考虑在$N$个节点的p2p网络中，存在监管委员会$R$人数$n\ll N$

假设委员会大多数诚实，委员会成员之间共享变色龙哈希函数密钥

• 区块链节点首先通过抗女巫攻击的方式生成身份（$pk，sk$）

• 执行去中心化自举协议协商委员会的大小（开销很大但是只执行一次）

• 网络中任何人都可以将编辑指令放进区块中来发起编辑请求
• 委员会成员根据编辑策略验证编辑指令
• 如果满足策略，委员会成员投票并作为交易广播
• 矿工检查投票并且将有效投票打包进下一个区块
• 来自不同委员会成员的投票超过$n/2$之后，每个参与者本地组合份额恢复变色龙哈希函数私钥，执行编辑
• 每轮epoch重新选举委员会，重新分发陷门密钥

Network and Threat model

同步网络，公有链广泛采用的假设，诚实节点之间的信道延迟至多为$\delta$

存在同步广播信道（区块链本身）

考虑PPT的拜占庭敌手，任意时刻腐化的敌手数量满足$\rho < 1/2$，被腐化的敌手可以任意偏离协议，发送错误的消息或者保持沉默

假设敌手slowly adaptive，敌手可以在每一轮开始或中间选择腐化的集合，但是直到该轮结束腐化才能生效

NITCH

给出非交互式变色龙哈希函数的构造和在RO下的安全证明

• 部分更新算法$Partial\ Adapt(sk_i,vk_i,m,m’)\to s_i=(i,c_i,\pi_i)$，输出更新后的份额$c_i$和对应的证明
• 部分验证算法$Partial \ Verify(pk,vk_i,s_i,m,m’)\to 0/1$
• $Combine(VK,(h,m,r),m’,\varepsilon) \to r’$，其中$\varepsilon=\{s_{i_1},\dots,s_{i_{ |I| } } \}$输出新的随机数或者空
  • 奇怪的是恢复密钥采用的不是原始的私钥份额，而是执行部分更新算法后份额

verification keys的作用

Instantiation

• 系统模型阶段

  • 每个节点建议自己的身份并广播
  • 协商出大小为$n$的委员会

  • 任何人可以发起RI并广播到区块中

    • 如何发布RI

      • 存储在区块中的话，相当于需要发起一笔交易
      • 如果不存在区块，需要一个单独的数据结构存储RI，因此节点本地有

    • 如果编辑交易和普通交易不可区分，不需要考虑

    • 如果出块者在打包交易时发现了编辑交易，为什么要打包进编辑交易呢
      • 设计激励机制

• DKG采用如下方案，只需要一轮通信，但无法保证均匀，用到了RO假设

  • 
  • Non-interactive and information-theoretic secure verifiable secret sharing
  • 此处第二个生成元的作用：公开可验证常数项的正确性，每个份额的正确性只有拿到份额的人可以验证
  • $sk=\sum a_{i,0},sk_j=\sum s_{i,j}=\sum f_i(j),pk=g_2^{\sum a_{i,0}},vk_j=g_1^{\sum s_{i,j} }=g_1^{sk_j},i\in QUAL$
  • 私钥份额$sk_j$即所有参与者多项式在$j$处的求值
  • 此处的$l_i^I(0)=\prod\frac{x}{x-x’} \bmod q$
    • 参考一篇博客 https://medium.com/nethermind-eth/a-tour-of-verifiable-secret-sharing-schemes-and-distributed-key-generation-protocols-3c814e0d47e1
    • DKG使用私钥而不泄露私钥是非常重要的

利用NITCH构造DRB

Construction

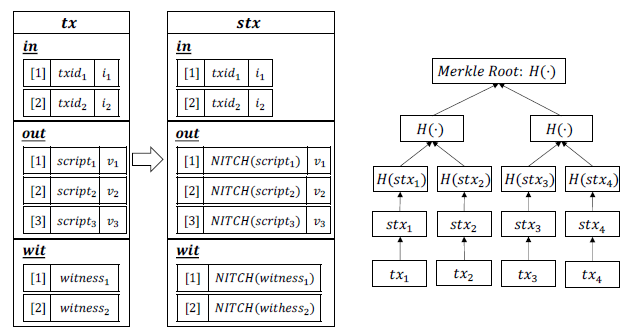
Shadow Transaction(stx)

• 目的：实现交易级的修改
• 将可修改的、能够插入任意数据的字段称为admissible fields $AF(tx,out.script,tx.wit)$
• 实际就是复制原来的交易，将AF字段设置为对应的变色龙哈希的值
• 带来两个性质
  • 可编辑性：交易的AF字段可以被委员会编辑
  • 不可篡改性：交易的stable fields无法修改（H是抗碰撞的）

The redactable blockchain Protocol

• Update local chain：每轮开始选择最长链进行本地更新
• 从链去掉末尾k个区块后，收集所有编辑请求
  • 将请求加入到RIP(research instruction pool)
  • 对编辑请求投票，更新RIP中的$(RI,\phi)\to (RI,\{vote\})$
• 收集投票：更新$(RI,shares\cup s_i)$
• 编辑交易：如果$len(shares)>n/2$，执行$NITCH.Combine$算法
• 扩展链：产生新区块并广播
• 编辑结束之后，其他用户可以提出新的编辑请求

Committee Evolution

随机数生成

$R^e$执行DRB为下一轮生成随机数串$\tau^{e+1}$，当前轮结束后揭示$\tau^{e+1}$

下一轮委员会选举

下一轮$e+1$开始时，每个参与者本地选择公钥和地址$(PK,IP)$作为身份

• 引进IP为了防止女巫攻击

能够发现PoW的解的参与者作为下一轮委员会的成员（公平性）

经过$\Delta$时间后，停止选举（如何保证委员会人数正确）

分布式密钥再分享

• 处理阶段

  • 每个$R^e$中的参与者$P_i^e$随机选择多项式$f_i(x)=sk_i^e+\sum_{j=1}^{t^{e+1} } a_{i,j}x^j$（注意此时用的是下一轮的$t$）
  • $P_i^e$广播$A_{i,k}=g_1^{a_{i,k}},k=0,\dots,t$
  • $P_i^e$计算份额$s_{i,j}=f_i(j),j=1,\dots,n^{e+1}$，发送$f_i(j)\to j$

• 验证阶段：验证发送的秘密份额是否正确，实现对委员会参与者的追责

  • 参与者$P_j^{e+1}$计算
  • $$g_1^{ s_{i,j} } \mathop{=}\limits^{?} \prod_{k=0}^{t^{e+1} } (A_{i,j})^{j^k}$$

  • 如果不成立，广播对参与者$P_i^e$的投诉

• 投诉阶段（抱怨2333）

  • 如果每个参与者收到超过$t^{e+1}$个投票就失去委员会资格，$P_i^e$收到投诉时需要重新发送$s_{i,j}$的份额，如果新的份额依然不通过则失去资格

• 恢复阶段

  • 计算公共验证密钥
  • $$\mathrm{vk}_j=\prod_{i \in U} \prod_{k=0}^{t^{(e+1)}} A_{i, k}^{\ell_i^U(0) \cdot j^k}, j \in \mathcal{R}^{(e+1)}$$

• 每个参与者本地计算私钥份额

  • $$\mathrm{sk}_j=\sum_{i\in U} (\ell^U_i(0)\cdot s_{i,j})$$

目的&收获

• 学习如何构造非交互式的门限变色龙哈希
  • 显然还是需要交互的
• 刷新委员会和密钥份额的区别
  • 抗女巫攻击的身份生成方案
• shadow transaction如何实现交易一致性
• 实现多项式插值的算法的加速
• 学习 decentralized bootstrapping protocol
• 记得学习https://missing-semester-cn.github.io/2020/

• 本方案要求本地存储两个数据库

  • redaction instruction pool：储存当前的编辑请求，超过门限就恢复秘密执行编辑
    • 如何保证这个数据库的同步性，可能有敌手宣称已经超过1/2
  • check value revocation list：存储区块最新的$r’$
    • 为了保证这个字段的一致性，区块头增加了$h=HASH(CVRL)$

• 方案的轮数是如何定义的

• 无法实现对区块的删除

• 具体出块者是谁