2012年BIU密码学冬令营-01-Introduction to Lattices
2012 BIU Introduction to Lattices
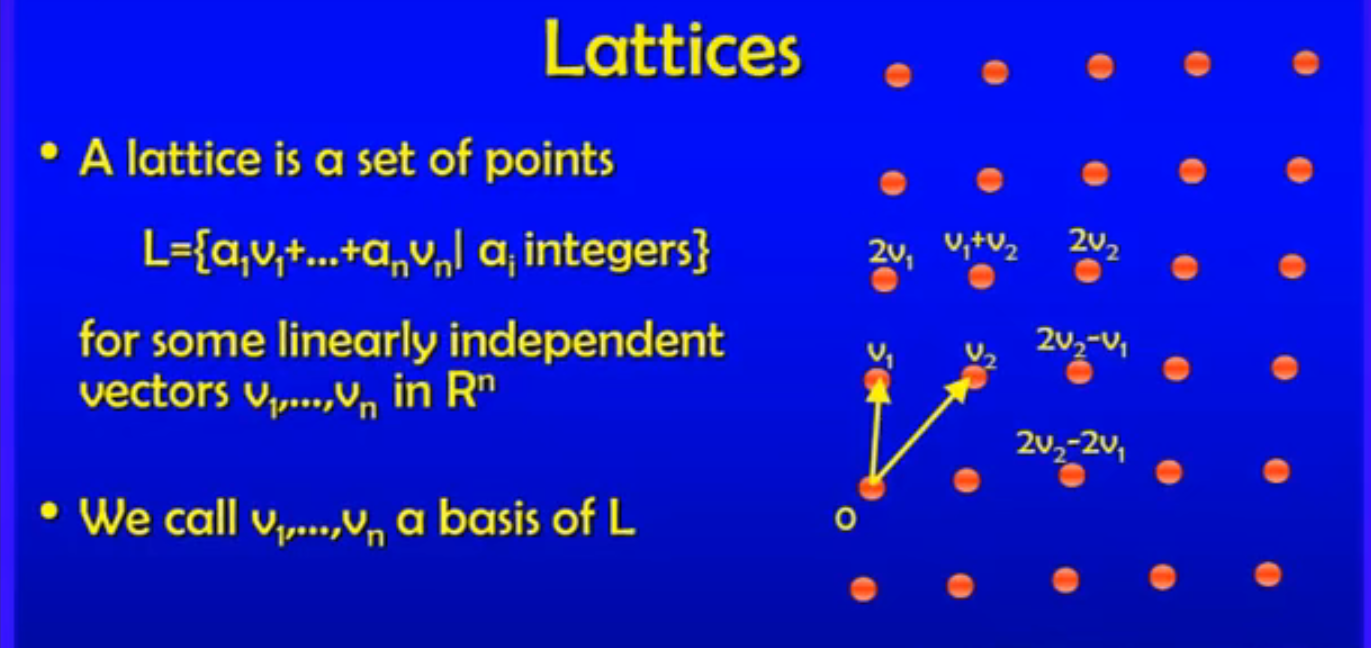
基底不唯一



格密码的安全是worst-case的困难问题
传统密码学是average-case的困难问题
格可以实现FHE


安全证明可以给出关于如何选择安全参数的提示
average-case的困难问题,比如如何选择N?
- 大质数$p,q$如何选择
- $p-1,q-1$的素因子应该足够大
- $p+1,q+1$的素因子应该足够大
- 实际上现在已经不太重要了
格不存在这样的问题



如果1%被破解了,所有格上的困难问题都被破解了,不需要考虑参数的选取

现在格密码的效率和RSA接近
- LWE SIS
- RLWE RSIS 特定代数结构,效率非常高,密钥长度KB级别,接近哈希函数的效率

两个定义,实际上等价 列就是基底
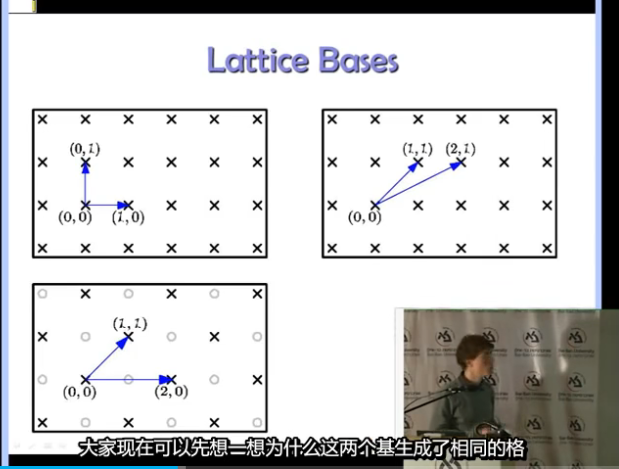
等价基底
如何寻找等价基底,能在基底上做什么
- 列变换 $v_i\leftrightarrow v_j$
- 取负值 $v_i\gets -v_i$
- $v_i\gets v_i +kv_j,k\in Z$
相当于右乘 幺模矩阵(unimodular 行列式值为1),对乘法封闭
两个格等价的条件


格的一些特征
一维空间的周期函数$f:\R \to \R$
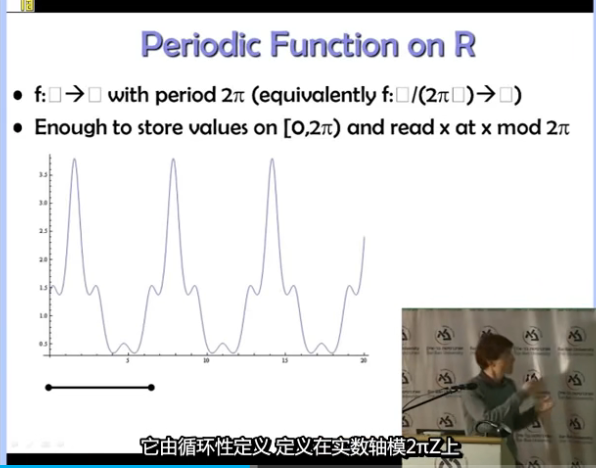
考虑高维空间,类似于循环群,只需要存储陪集


格的基本区域
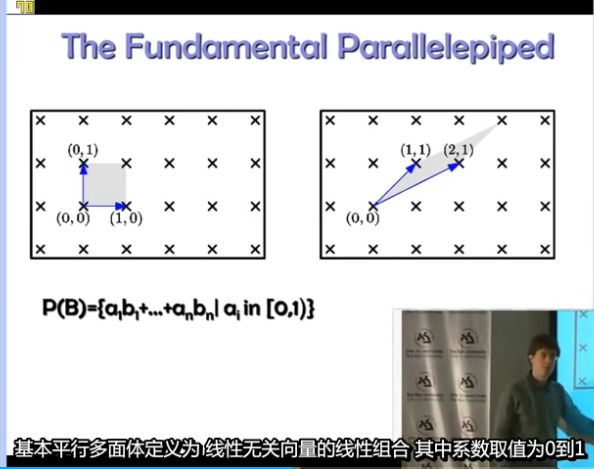
给定基,可以定义基本平行多面体 就是一个基本区域,恰好包含陪集中的每一个元素
基本空间的等价定义:基本空间内不存在两个等价的空间点,仅包含所有不等价陪集内的点集

寻找空间点的一个表示,实际上是在做模 基本平行多面体
存储的实际是点和格的相关性,当点在格上,模P(B)后得到原点

实际上平行多面体的形状无重要,可以用任意多面体标识格,不是所有基本区域都是平行的

基本区域的面积必须相同,对平行多面体也成立,可以把平行多面体内的点映射到另一个平行多面体中
格的行列式定义为基生成的平行多面体的体积$|det(B)|$
格的行列式表示了格点的稀疏程度,密度

连续极小,最短向量(集合)
一般距离是欧几里得范数

一般指关心$\lambda_1 $
$\lambda_n $是线性空间的基
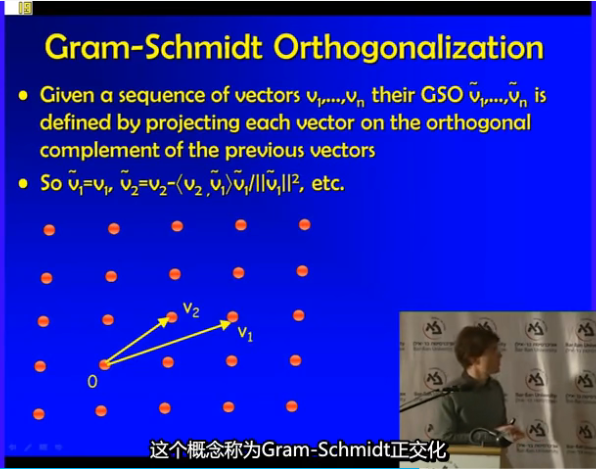
注意$\tilde{v_2}$并不是格点
正交基也是基本区域

从正交向量集到规范化正交集,是线性代数层面的基而不是格的基

QR分解
可以证明施密特正交区域是基本区域

证明引理1:三角形行列式等于主对角线上元素的乘积
证明引理2:对最后一列的系数取非0,其他所有项系数取0,则 $\lambda_1\geq \tilde{v_n}$;同理当倒数第二列系数为非0,其他所有列系数为0,$\lambda_1\geq \tilde{v_{n-1}}$ ,永远存在非0系数,实际得到了$\lambda_1$的下界
Minkowski‘s theorem
袋鼠的面积大于格的行列式

S必须是关于0点对称的凸集合,存在一个非0格点,因为0永远在S中

证明:将S缩小一半,体积缩小$2^n$,$z_1-z_2\in \Lambda $
由于$\pm2z_1,\pm2z_2 \in S,2z_1-2z_2$的中点 $z_1-z_2\in S$

说明了格中至少有短向量
等价推论:任意行列式为1的格,必然包含长度不超过$\sqrt{n}$的短向量
考虑半径为$\sqrt{n}$的球,球的体积大于$2^n$
现在格中找短向量的方法都是数学方法,基于格的密码学方案假设是不知道如何高效求得格的短向量
Blichfeld定理是存在性定理,没有给出如何求
计算困难问题
简单问题
给定格基$B$和向量$v$,检查$v$是否在$L(B)$
解法:高斯消元检查系数是否为整数
给定格基 $B_1 B_2$,判断$L(B_1)=L(B_2)$
解法:根据之前的定理,$B_1 = B_2\times U$,$U$是幺模矩阵
另一个解法:取基$B_1$中任意一个向量,检查是否属于另一个基;如果所有基向量均在$L(B_2)$,再检查$B_2$中所有向量是否在$L(B_1)$
结论是代数问题很简单,但是几何问题很困难

困难问题
最短向量问题,SVP
给定基,求最短向量
密码学常用的是近似最短向量问题,求得最短向量的$\gamma$倍的向量
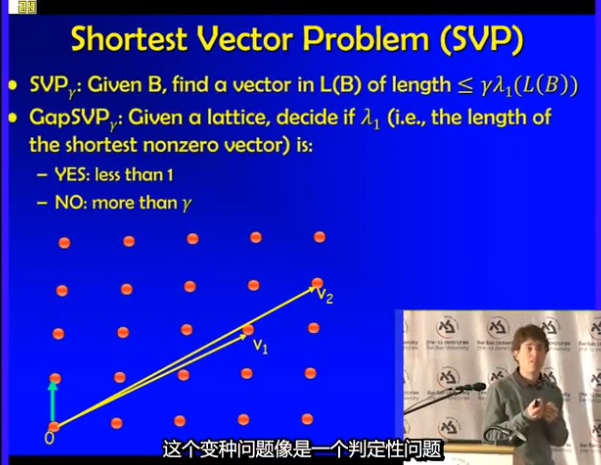
变种:给出近似最短向量的长度即可(类似判定小问题
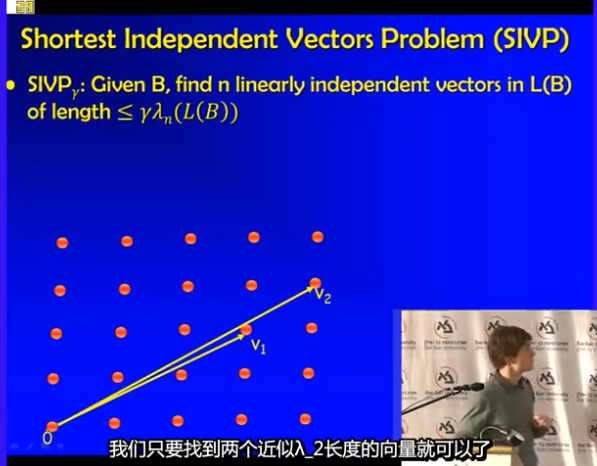
最短独立向量问题,SIVP
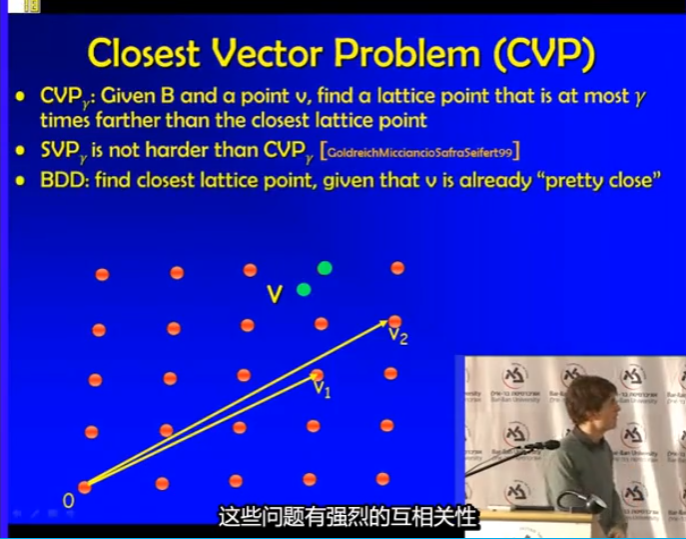
最近向量问题,CVP
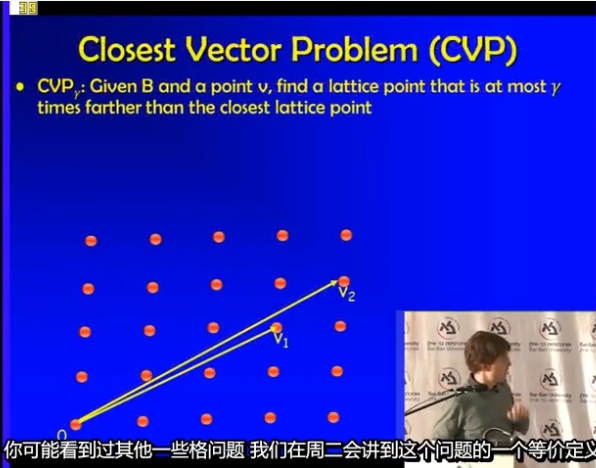
SVP不比CVP更困难,CVP解决能解决SVP

LLL是多项式时间算法,输出短向量,近似因子接近$2^n$,当$n$接近500,输出向量不够理想

