FSS

Elette Boyle’s lecture on FSS from 12th BIU Winter School)

Function Secret Sharing

简单介绍加性秘密分享

考虑分享一个秘密的函数，份额通信量非常小（compact）

FSS is compressing the truth table of additive secret sharing

3Hours：

• 定义和性质
• 构造
• 扩展和应用

definition

• $Gen(1^\lambda,f)\to(f_0,f_1)$ some times $k_0,k_1$

• $Eval(b,k_b,x)\to y_b$, $x$ is the public input,$y_b$ is the output share

  satisfying

• secrecy (semantic security): $\forall f,f’ \in \mathcal{F}, \{k_b \in f\} \approx \{ k_b \in f’\}$

  • statistically close
  • relaxed bond: relaxed on hardness problem
  • simulation security

• reconstruction: $y_0+y_1=f(x)$

  • other forms are acceptable

• FSS For All functions(truth table)

  • using additive secret sharing but the share size is $O(2^n),where \ input\ len\ is\ nbits$

• Linear functions over ring $R$

  • using coefficients additive secret sharing

• polynomials

  • also using coefficients additive secret sharing

Notes: secret linear combination of public function of x and All the constructions above are information-secure

for some classes of functions can only get computational security

• Point functions
  • $f_{\alpha,\beta}(x)=\alpha $ only when $x=\alpha$, else eval 0

Sample Application

similar to PIR

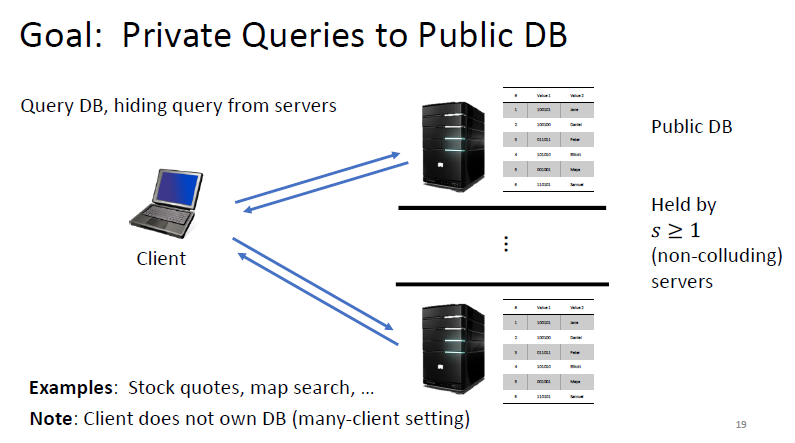
2服务器 计算安全的PIR的结果和FSS结果不谋而合 （corollary）

AES is unbreakable, means lightweight crypto

FSS for points Functions \to 2- server PIR

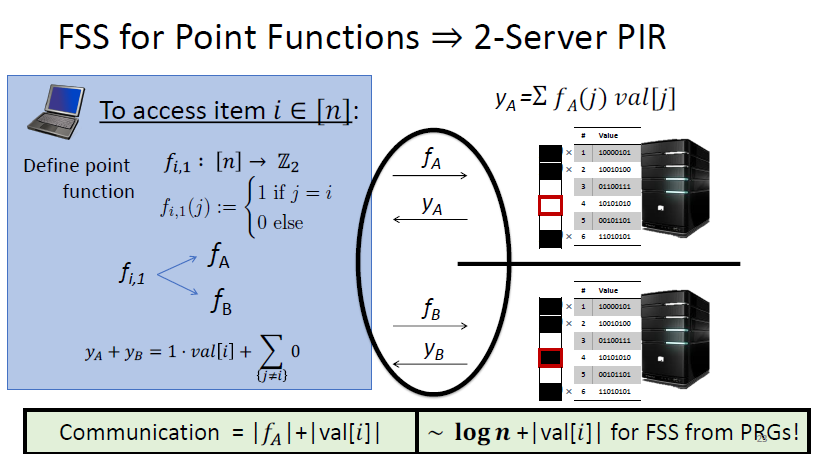
正确显然成立，黑色框是0的秘密分享，$y_A\ y_B$求和后只剩下$val[i]$

FSS for Point Functions ⇒ Private Increment satisifying p

Q: garble circuits as a weak case of FSS

A: yes, reconstruction is not additive, former applications won’t go directly

Q: how to complete private read and write an the same time

A: Not possible. reading needs server to store same data, writing needs server to hold shared data, changing sever numbers may

Q: point functions can’t be described as low degree polynomial having FSS for low degree polynomials and FSS for distributed point function

Construction

point functions

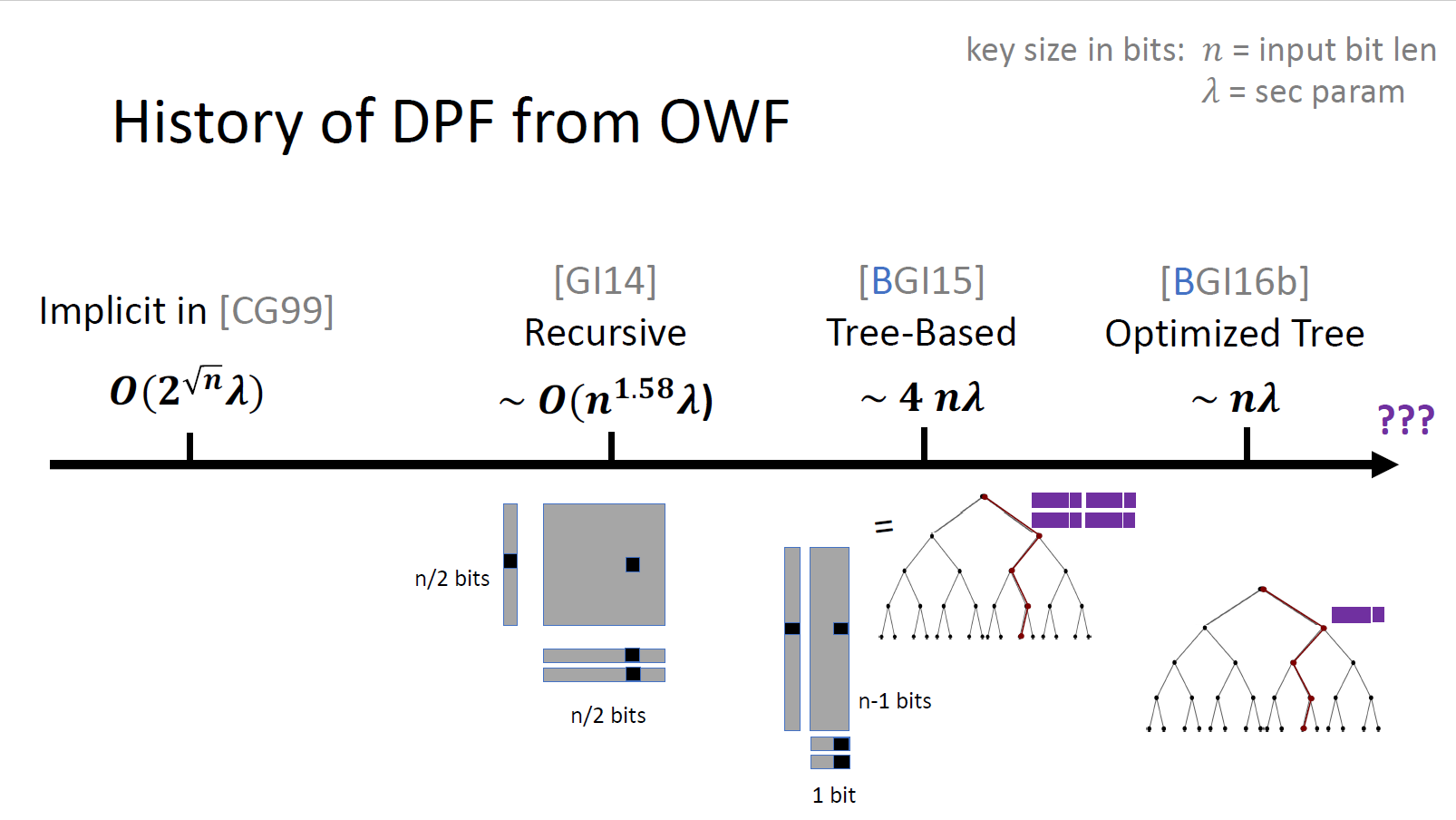
DPF的第一个构造来自于[CG99]对PIR的构造，$n$是函数输入的bits

comparison functions