Alleysira's blog
0%

GearBox

Posted on Edited on In

GearBox: Optimal-size Shard Committees by Leveraging the Safety-Liveness Dichotomy

David B, Magri B, Matt C, et al. GearBox: Optimal-size Shard Committees by Leveraging the Safety-Liveness Dichotomy[C]//Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security. 2022: 683-696.

分片是克服区块链可扩展性难题的新兴技术，没有分片，每个节点都必须监听和处理所有账本的信息

分片的基本思想是并行化账本协议：将节点划分为子集处理，通过执行轻量化的账本协议实例来处理部分原来的工作，分片越小，因为提高了并行化，分片共识协议的开销小，效率越高

沿着这个脉络，本文提出了一个新的方案——采用安全性-活性二分法，在分片共识种将活性和安全性拆分开，允许动态调整分片参数实现在当前腐化比例下最优的效率

  • 首先建立一个相对小的分片（诚实节点的比例可能很小）
  • 在共识协议中仔细地用安全性来trade-off活性，来容忍小的诚实节点的比例，但不丧失安全性
    • 困难性在于分片想要获得活性，最坏情况下需要更高的诚实节点比例
    • 采用一条永远满足活性和安全性的control chain来检测活性失败
    • 分片被检测出不满足活性的情况下 重新设置为更大的分片大小和活性容忍度直到满足活，保证所有分片永远安全并且效率最优
  • 具体数据：10000参与方，30%的腐化比例，60-bit安全，之前的设计要求每个分片超过5800个参与方保证安全性，本方案最坏情况下需要1713节点，最好情况下需要35个节点

在高并发的执行环境下，保证账本协议和子协议在通用组合下的安全性非常重要，为了证明协议的安全性，本文给出了分片账本、控制链和分片共识的理想的功能，形式化并证明了在UC框架下的安全性

Introduction

阻碍区块链大规模应用的障碍之一是较低的交易吞吐率，分片是克服这一困难的解

60bit安全的含义：保证安全性的概率为$1-2^{-60 } $

旧的安全性带来的参数要求：

  • 10000参与方，33%恶意，60bit安全，分片的大小为5886；
  • 30bit的话，分片大小为3000；

为了保证分片大小为几百，可以考虑降低安全性

区块链的安全性包含2个性质

  • 活性：交易在一定时间内会被打包，活性门限记作$L$
  • 安全性：节点对输出的交易序列达成一致，安全性对应的门限记作$S$

现有方案考虑的是最坏情况下的界，导致了活性和安全性的界相同

贡献

采用活性和安全性分开的思想，企图实现尽可能小的分片大小，主要面对半同步网络（可以适用于同步网络），协议开始时采用激进的设置，活性门限较低（$S=0.89,L=0.05$），这样的设计会导致较小的分片大小，但是分片可能会死锁，因此引入了独立的一条链control-chain来检测分片的活性，分片需要向控制链发送heartbeat心跳交易，控制链可以解散死锁的分片，然后建立一个新的带有更高活性的分片，迭代直到寻找到了能够找到保持活性的最小分片大小；另一方面，没有检测到死锁时，可以动态降低分片的大小，已达到最优的分片大小

下面是两类实施本文方案的方法

  • 部分同步网络

对于10000个节点，$L=0\%,S=99\%,Size=35\to L=30\%,S=39\%,Size=1713$

  • 混合模式

能够运行同步的CC容忍50%的恶意敌手比例，在分片内为部分同步网络，能够切换到同步网络下（25%的恶意敌手之前）

静态与适应性安全：当敌手能够立即腐化超过半数委员会成员时，基于诚实大多数委员会保证安全的分片协议都基本会失败。Free2Shard能够容忍动态敌手，假设的安全模型不同，无法直接比较。如果假设腐化有时间延迟，可以通过重新选择委员会的方法保证安全性。

跨片通信：本文的分片可能丧失活性，依赖control-chain进行保证，基本思想是将相关交易的merkle树值包含在心跳信息中

UC形式化：给出了分片区块链的理想功能，证明了UC-realize，本文是第一个实现了任意组合下的安全性的分片区块链

Technical Overview

  • Control chain 建模为一种定时的账本功能，对消息进行排序、打上时间戳。更形式化来说是全排序的广播，带有一致性和时间戳保证
    • CC被所有参与方执行，但是仅存储分片的大小
  • 分片：建模为账本功能，参数包括分片委员会的大小和敌手比例
    • 协议不保证领导者恶意时的活性，因为可以利用cc进行恢复
      • 代价是需要经常更新委员会，解决无响应leader的机制更加复杂了
  • 协议：协议的目标是实现一种分片的账本，开始时所有分片的委员会尽可能小，利用CC进行初始化和委员会重新选举
    • 协议的核心在于心跳消息，是的CC能够实时评估分片的活性，通过要求分片周期性发送区块的哈希值来实现，每次发送一个区块会设置一个超时时间，如果下一个有效的区块没有按时到来，分片被认为死锁
    • 当分片死锁之后，采用更大的委员会重启来保证活性

目前对于分片区块链的研究，尤其是来自工业界的，对安全性的理解是启发式的，没有形式化的安全证明，因此这部分介绍少数几个知名的分片区块链

推荐综述[AFT19]Gang Wang, Zhijie Jerry Shi, Mark Nixon, and Song Han. 2019. SoK: Sharding on Blockchain. In Proceedings of the 1st ACM Conference on Advances in Financial Technologies, AFT 2019, Zurich, Switzerland, October 21-23, 2019. ACM, 41–61.https://doi.org/10.1145/3318041.3355457

分片区块链协议

  • Elastico是第一个分片区块链，同步 每轮节点解PoW来确定委员会成员，puzzle的随机性来自于上一轮，作者希望实现小的分片委员会大小，但是6轮后不安全的概率为97%，导致协议的不安全
  • OmniLedger基于Elastico，PoW引入了身份，但是仅能在敌手小于25%实现高效率（能支持33%但是效率较差）
  • RapidChain作为同步的分片协议，能够容忍1/3的恶意敌手，每轮选举委员会，委员会及负责生成随机数
  • Monoxide提出了可横向扩展的区块链，提出了若干独立的并行的链，将网络的通信、计算和存储分散到不同区域内，当出现跨区交易时，采用最终原子性技术来保证一致性
  • Avarikioti[1]等人的工作提出了一个分片区块链的安全框架，基于比特币骨干协议，但是该框架不满足可组合性

共性问题

  • 对于具体参数，委员会的大小必须足够大来保证分片的安全性
  • 之前的文章没有考虑通用可组合性下的安全性

Preliminaries

安全模型

需要给出同步和部分同布网络下UC安全的记号，假设参与方能够访问可靠的网络功能，时延上限为$\Delta_{NET}$，假设存在理想的签名功能，为了简洁，不给出所有功能的模型，而是给出参考文献，安全地实现本协议是一个很难并且独立的任务

  • 时间功能$\mathcal{F}_{CLOCK}$本质上等同于假设完美的同步 离散时钟，利用time slot表示两个时间刻度之间的间隙，也称tick，两个诚实参与者$P_i,P_j$分别在$r_i,r_j$时刻，则满足$|r_i-r_j|\leq 1$，参与者能够执行任意多项式复杂度的计算
  • 网络$\mathcal{F}^{\Delta_{NET}}_{N-MC}$ 允许参与者进行多播消息，时延上限为$\Delta_{NET}$，当参与者对该上限不知情时是部分同步网络
  • 敌手模型 考虑被腐化的敌手是静态的，5.3有扩展到适应性腐化的内容

Ledger Functionalitiies

Sharded Timed Ledger

时序账本的账本$\mathcal{F}^\Delta_{BD-TL}$ 允许所有参与者输入消息，消息会被全局排序，提供时间戳，能保证一致性和活性

image-20230819180300128

一致性要求了诚实节点的输出一定存在前缀的关系；活性要求发送的消息在$\Delta$时间内会出现在诚实节点的消息列表中

定义 $\mathcal{F}^\Delta_{BD-TL}:=\mathcal{F}^{\Delta,1}_{BD-STL}$，是仅有1个分片的特殊情况

时序账本可以用BFT类共识Hotstuff 或者 PoW的区块链来实现

分片的时序账本：简单来说是多个并行的时序账本的集合，每个独立的账本都是一个分片，假设分片的数量固定，每个分片有独立的标识符$sid$，以下给出$\mathcal{F}^{\Delta,1}_{BD-STL}$的形式化定义

image-20230819182237876

和传统的链质量 链增长链前缀定义不同，看起来更简洁（？

本文的形式化更接近于 基于性质的定义，而不是传统的UC安全的定义

输出给敌手的含义是 对应的行为会向敌手泄露对应的行为发生了

Shards

本质上一个分片就是一个账本，本文的定义为$\mathcal{F}^{s,\mathcal{L},\Delta}_{SHARD}$，由委员会的大小$s$，活性相关的敌手结构$\mathcal{L}$定义

敌手结构$\mathcal{L}$是一个集合，指分片功能必须在$(P_{i_1},\dots,P_{i_t})$为腐化节点时保持活性，其中$(P_{i_1},\dots,P_{i_t})\subset \mathcal{L}$

分片内的节点可以通过SEND命令发送交易，可以利用CLOSE命令关闭分片

分片需要保证的性质分别是

  • 证明的完备性：只有正确的描述才能产生有效的证明
  • 抗审查性：防止敌手排除特定消息
    • 是活性不满足的情况下的一种保证

image-20230819184837902

image-20230819185706285

Committee selection and shard consensus

分片的核心部分，讨论如何实现随机信标并分析委员会的大小

Committee selection

委员会选择功能：$\mathcal{F}^{\mathcal{P,U}}_{COMSEL}$，其中集合$P$是参加委员会选择的节点，集合$\mathcal{U}$是委员会节点被选择出的集合

U和P的区别不明确

image-20230820091849435

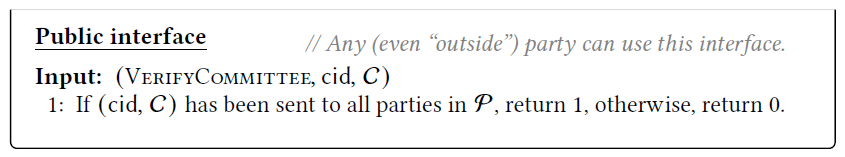
image-20230820091905102

给出的选择方法看上去是随机选，实际上公有链上需要基于资源进行选择，因此需要一个虚拟的参与方集合 $\mathcal{U}$，这个集合是根据节点的资源生成的，因此不是简单的随机选

利用random beacon实现 $\mathcal{F}^{\mathcal{P,U}}_{COMSEL}$，所有参与者可以均匀随机选择随机性并且验证，具体实现是利用随机信标从$\mathcal{U}$中随机选一个$s$长的序列即可

Remark：目前实现中$\mathcal{U}$对应的是所有参与者，即一个参与者可能会出现在多个分片中，实际需要更复杂的机制来限制一个节点能够被分配的分片个数

其他实现委员会选择的方法：PoW和PoS，PoS可以分为：

  • 基于硬币投掷的随机性信标的均匀随机委员会选择
  • 基于可验证随机函数的偏倚委员会选择（不满足抗偏置性，效率更高）

Shard Consensus

实现3.2中分片功能

$t_L$是活性能容忍的腐化节点数量，对应的安全性为$t_s:=s-2t_L-1$，仅在对应委员会大小下安全

调用$\mathcal{F}_{CT}^{\mathcal{P,D}}$能够获得大小为$s$的均匀随机的委员会，委员会的第一个成员作为特殊的leader，称为sequencer，周期性地提出新区块，如果至少$s-t_L$个人签署则认为有效

传统的BFT有换主的协议，本协议有外部的利用cc进行更换委员会的方式，不需要换主机制

因此分片活性的条件是至多$t_L$个腐化节点与领导者诚实

为了保证抗审查性，每个参与者发送新交易时包含若干旧交易，如果排序者没有包含这些就消息，拒绝为区块签名（丧失活性）

同样可以实现带有换主的分片共识，考虑到直接更换委员会效率较低，对应的功能为

确定委员会大小

分片协议需要获得最小的委员会大小$s_{min}$来保证腐化节点的数量小于给定的门限

超几何分布的形式，其中n是节点总数，s是委员会大小，$t’$是门限

最大的腐化比例为$t’/s$，能够求出满足$\operatorname{Pr}\left[\text { FAIL }_{t^{\prime}, s}^{t, n}\right]\leq 2^{-\kappa}$的 $\kappa$，给出了python代码如何计算$\kappa$

委员会大小随着安全性要求指数级增长，因此降低诚实节点比例要求能够显著提高效率

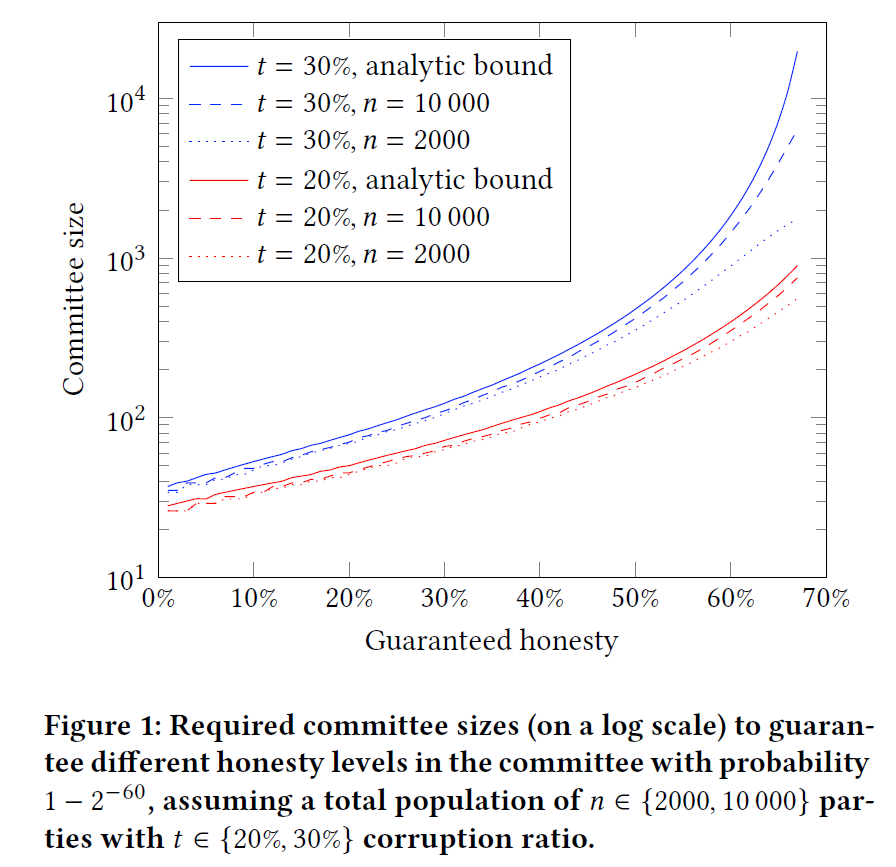
image-20230820101337925

表一给出了不同活性和安全性门限下的最小的委员会大小

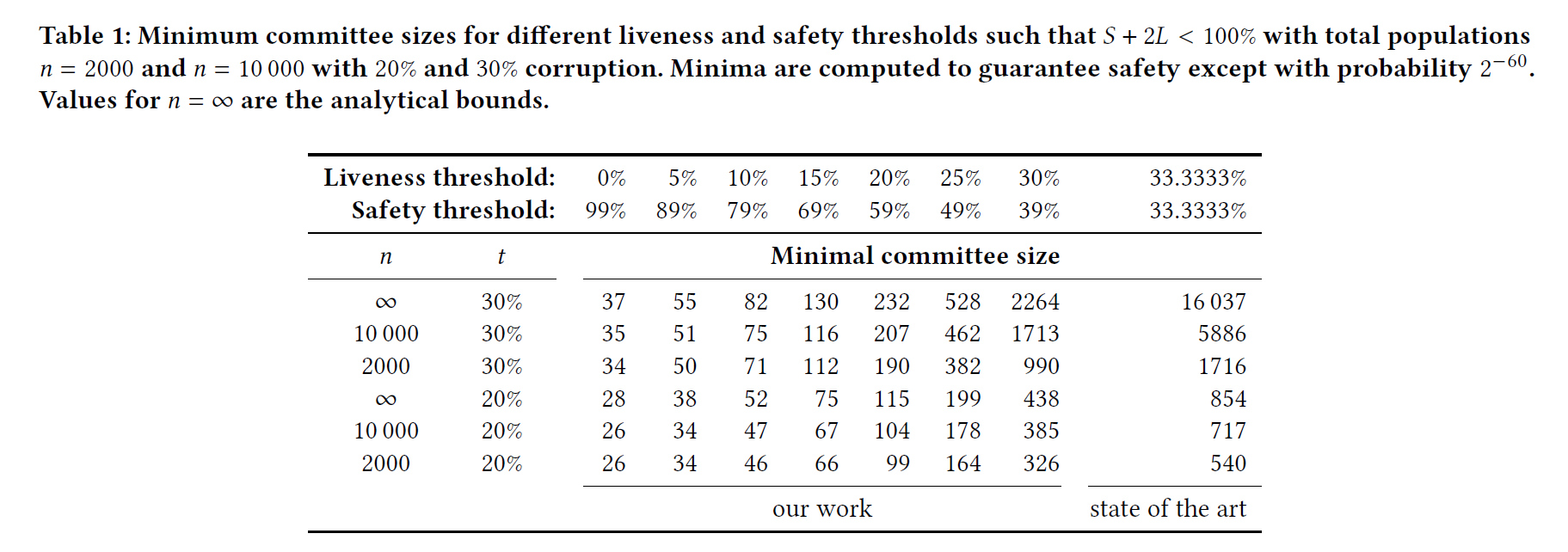
image-20230820103157673

Constructing a sharded ledger

Overview

为了实现$\mathcal{F}^{\Delta’,v}_{BD-TL}$，利用$\mathcal{F}^\Delta_{BD-TL}$作为控制链，$\mathcal{F}_{REPO}$存储分片确定的账本和之前的状态

反映了至少需要一方始终存储每个分片的状态的事实，分片功能有多个档位，即$\mathcal{F}_{SHARD}^{s_1,\mathcal{L},\Delta},\dots,\mathcal{F}_{SHARD}^{s_l,\mathcal{L},\Delta}$，其中委员会的大小逐渐增大

每个分片的共识协议 网络延迟和 活性结构均可以不同，分了方便分析固定了活性结构，延迟，活性保证$\gamma>0$

GearBox能够保证两个性质

  • 安全性：对于每个大小为$s_i$的委员会，$\mathcal{F}_{SHARD}^{s_i,\mathcal{L},\Delta}$不满足安全性概率为$2^{-\kappa}$
  • Eventually live 最终活性：$\mathcal{F}_{SHARD}^{s_i,\mathcal{L},\Delta}$满足活性概率至少为$\gamma$

首先运行$\mathcal{F}_{SHARD}^{s_1,\mathcal{L},\Delta}$观察是否满足活性，如果丧失活性则切换为$\mathcal{F}_{SHARD}^{s_2,\mathcal{L},\Delta}$，到达最大档位之后就是重启了

最坏情况下，$L=0.3,S=0.39$ 依然强于现有的共识方案

分片区块链协议$\Pi_{BD-STL}$

检测活性失败的方法可以归纳为几类

  • 分片管理：$\mathcal{P}$中所有参与者执行的协议，为了维持分片的活性
  • 分片操作：分片委员会成员的行为，仅执行与当前委员会相关的分片管理行为

获得输入后，参与方执行实现了对应接口的指令

经典的一页协议

image-20230820111300956

image-20230820111322916

image-20230820111404496

定理5.1：以上协议在部分同步网络，静态敌手假设下 在 实现了UC 功能$\mathcal{F}_{BD-STL}^{\Delta’,v}$

image-20230820112558207

扩展

  • 降低档位
  • 适应性和移动腐化模型：重新选择委员会

跨片交易处理和通信

本文不给出形式化的跨片通信机制的介绍

因为分片很可能重新启动，分片的交易不能立即认为有效，需要依赖控制链的CC交易，后续给出将gearbox利用到现有方案的方法

  • Atomix（OmniLedger的跨片交易处理机制）：分片A的用户向发起到分片B的交易时，首先在A内发起export交易锁定金额，当export交易在A中被记录后，用户向B发送证明证明自己的交易被A接收了
    • 如果采用gearbox，可能导致A中的金额被锁定，B中被解锁，但是A在发送heartbeat之前崩溃了，导致双花
    • 改进：用户的证明还需要证明该交易已经被CC确定了
    • 分片的性能不受制于CC，因为一个heartbeat消息能够包含分片内的所有交易，即和跨片交易数量独立
    • image-20230820114026946
  • 分片委员会驱动的跨片交易处理：分片的leader直接发送证明，开销转嫁到leader
  • 向包含了证明的用户发放奖励，如果用户和leader都未能对跨片交易给出证明的话，存在激励机制鼓励其他用户进行

Instantiations

Instantiation of Timed Ledger

之前都是模块化的设计，后续给出一个具体的协议

采用Hotstuff进行$\mathcal{F}_{BD-TL}^{\Delta}$，因为是固定换主的协议，但是不提供时间戳，leader将当前时间作为时间戳加入（假设weakly synchrnized clocks）

因为并不是所有的参与者需要从CC读写，CC需要满足1/3的安全性，最大为16037

Instantiation of Shard Consensus and Gearbox

可以选择一种没有领导者替换或者像Hotstuff这种实现了领导者轮换制的共识协议，后续的分析主要是Hotstuff

具体可以选4个档位，活性的门限设置为10% 20% 25% 30%

Instantiation of Randomness Beacon

网页做的很好看

image-20230820151942150

  • 可以采用外部PoS生成的公开可验证的随机数

为了使用一种自给的方案，而不是依赖基于Hotstuff的CC，传统的PoS随机信标

UC安全的PVSS(ALBATROSS)要求每个参与方417120模幂运算，需要在CC链上写21.2Mbytes

VRF的效率更高，2112模幂+0.065MBytes的通信，然而存在偏置性，可以通过轻微增大委员会大小来减轻开销

Efficiency Analysis of Overall Protocol

为了活性需要选择的委员会个数

  • 实际的敌手腐化比例为10%
    • 需要leader诚实，概率为90%
    • 预期的委员会个数为2
  • 实际的腐化比例为30%
    • 选择出委员会中敌手比例不超过30%的概率是0.5
    • 诚实领导者的概率为70%
    • 期望的委员会个数小于6

延迟和吞吐量

基于Hotstuff的实验结果,仅支持128节点，对后续的结果进行了推理

CC链的payload限制为128字节

延迟大概是$l=0.37s+6$，其中$s$是委员会的大小，约为6s

吞吐量计算公式约为$t=2400000/l$，约为404msg per sec

实际处理交易的分片的大小为1024Bytes

延迟大概是$l=0.67s+20$，其中$s$是委员会的大小，吞吐量计算公式约为$t=2400000/l$

委员会的大小取82, 232, 528, and 2264，延迟对应为75 175 374 1537 ms，吞吐量为32000,13714,6417和1561，实际的带宽取决于CC链的带宽

可扩展性和分片数量的界

由于HotStuff具有线性通信复杂度，而本文的委员会大小是有限的，因此我们的协议在通信复杂度方面具有可扩展性。

实际的分片数量受CC链的吞吐量限制，若CC链的吞吐量为400，分片每10s发heartbeat消息，则，能支持4000个分片，因此不支持无限的可扩展性，如果确实需要无限可扩展性，可以考虑采用多条CC链

实验参数的分析

目标：2000节点，单片共识支持500个节点，单片错误概率小于$10^{-18}$，可扩展为4个分片（但好像不是我们的任务）

image-20230821092708085

image-20230820185618306

image-20230820185137655

以下是K=18的结果

image-20230820185118323

Video

链接：GearBox: An Efficient UC Sharded Ledger Leveraging the Safety-Liveness Dichotomy - YouTube

image-20230818184146046

带入实际参数，想要满足安全性的话需要的节点太多，只能分2个片

image-20230818184310857

如何进行优化

  • 降低全局敌手比例的界，找到实际中更精确的界
  • 提高失败比例，比如40bit安全性可接受？

image-20230818184637028

仍然不够，实际的BFT算法超过1000节点效率就不高了

终极目标是：安全性不变，通过更少的分片内节点的数量，实现更高的效率（吞吐量）

如果想要保证安全性（全局敌手比例+60bit），只能从片内敌手比例入手了

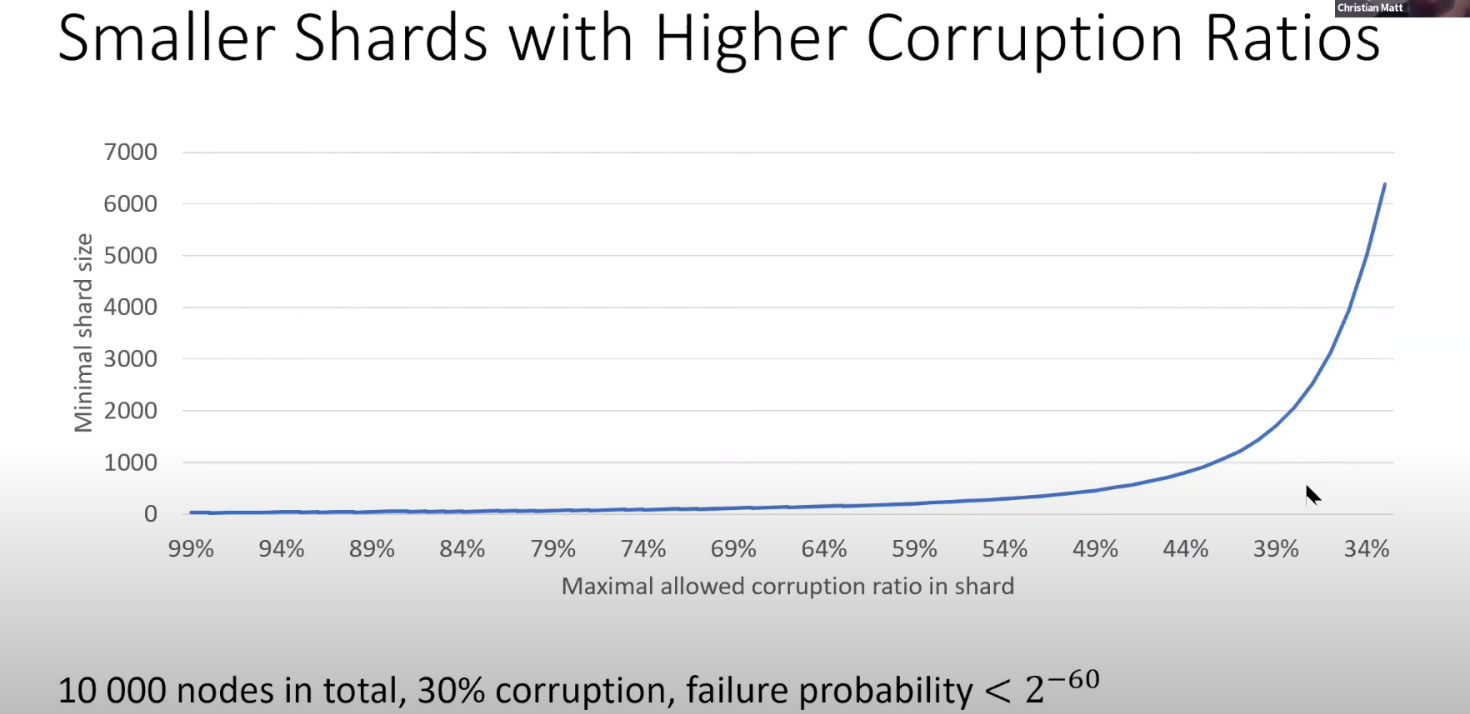
image-20230818185205913

当支持的片内敌手比例达到44%以下后，就需要1000个以上的节点了

难道不需要片内30%的比例来保证安全性吗？

本方案给出 安全性和活性二分法 来解决这个问题

image-20230818185503978

如果$L=S$，就是之前的解

对于活性，假设诚实节点不会为冲突的区块签名，则活性可以归纳为

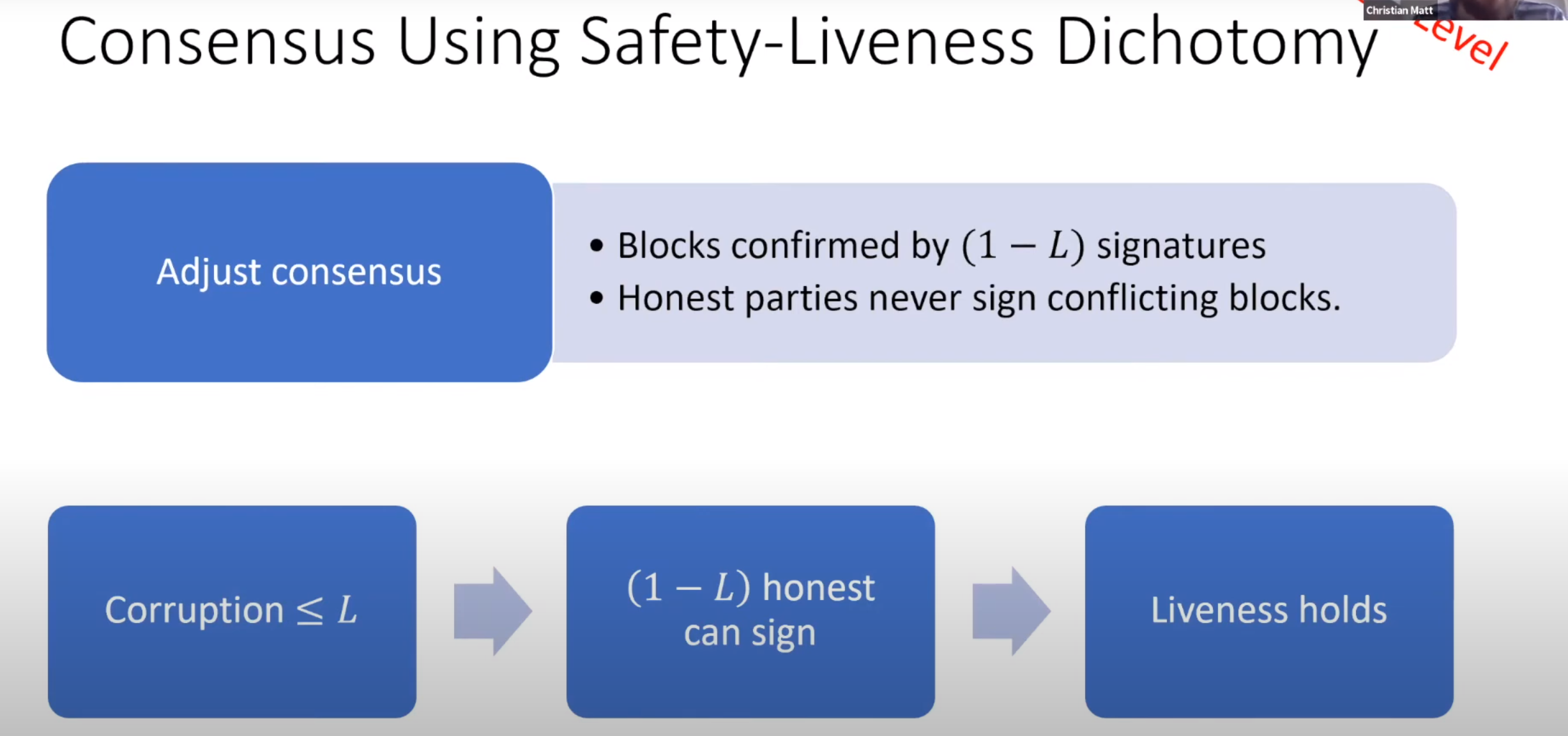
image-20230818190028903

对于安全性，已知$2L+S<1$成立，白色部分是剩下的部分

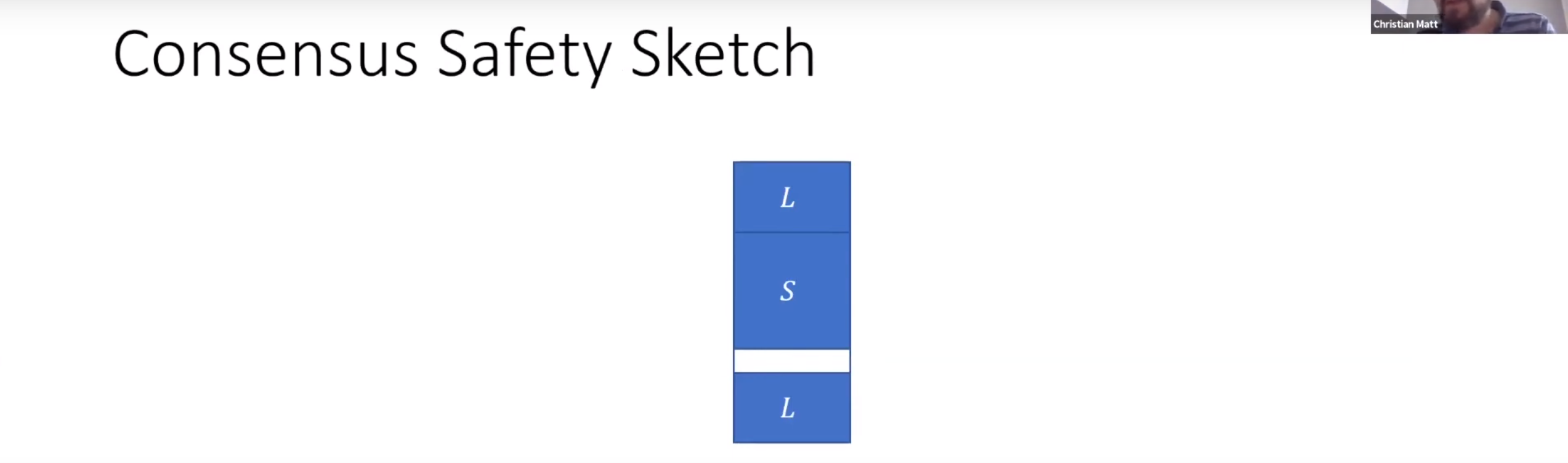
image-20230818190256418

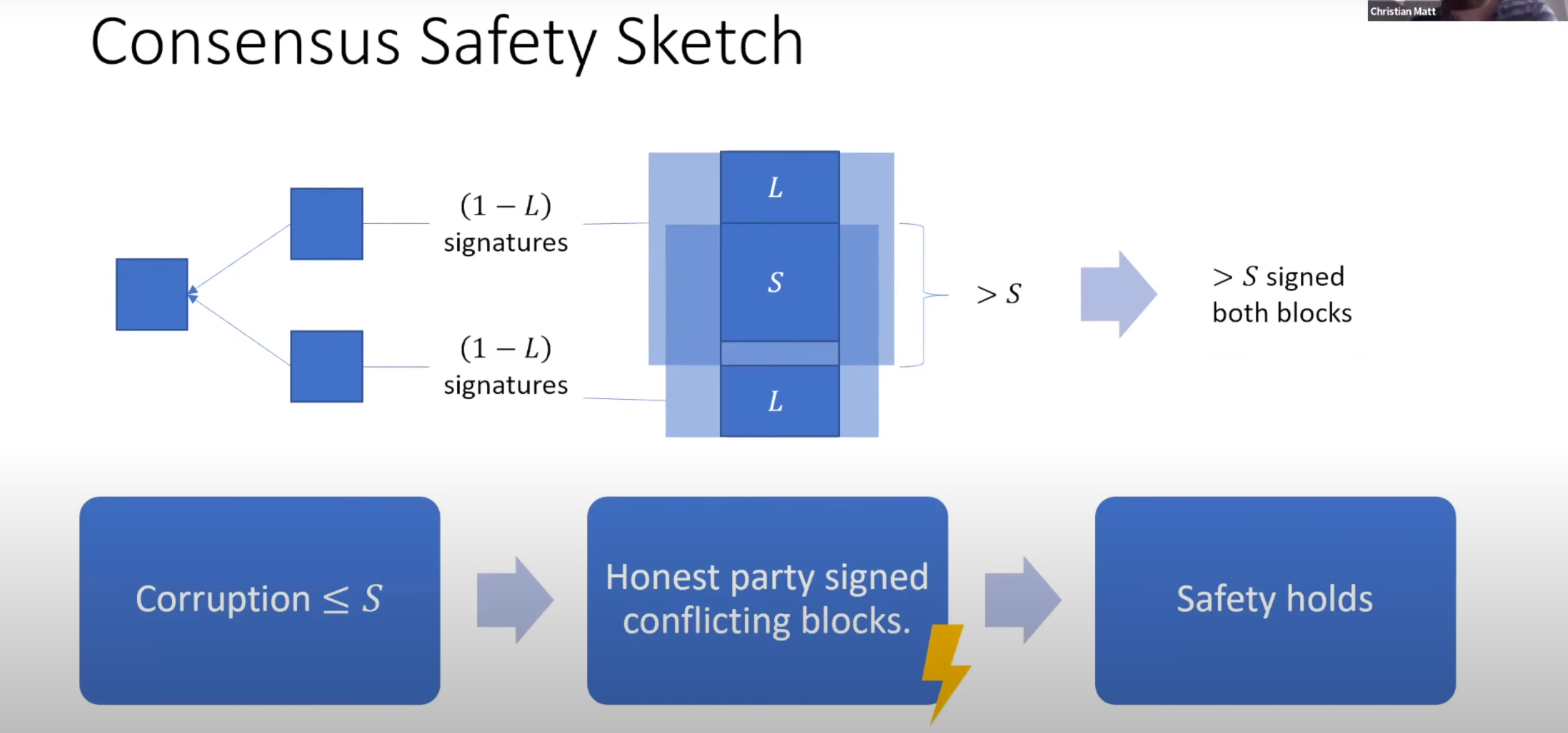
假设2个区块冲突了，即不满足安全性，则每个都被至少$1-L$个签名了，则同时为2个区块签名的节点数量（交叉的部分）大于$S$，即存在诚实节点为冲突的区块背书了，产生了冲突（不成立）

则得出结论：敌手比例小于$S$，能够满足安全性

问题：没有给出$2L+S<1$的根据，在完整版论文的附录A

image-20230818190506447

实际中一个更好的协议需要考虑

  • 最坏情况下，能够达到30%（半同步
  • 一般情况下敌手比例会小于30%
  • 当敌手比例小的时候，有更好的效率

image-20230818191344481

本方案类似于汽车的手动挡，安全性一定保证，活性以概率保证（丧失活性的概率是$2^\kappa$，以下是实现的结果

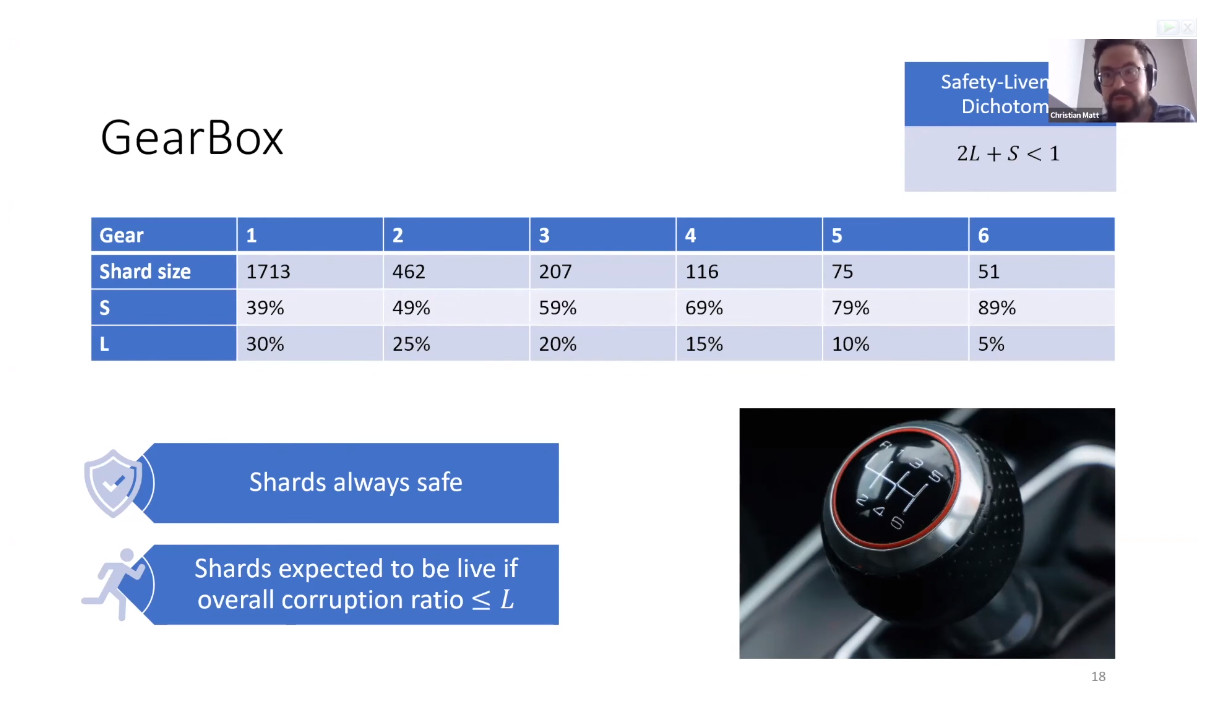
image-20230818191416876

难点在于想要实现活性，但是不知道具体的敌手比例

解决方案是利用一条监控的链， 采用$S=L=1/3$，能够检测出活性不满足的情况

还需要解决死锁问题（不是传统意义的死锁，指丧失活性后。当分片需要调整安全性，换挡）

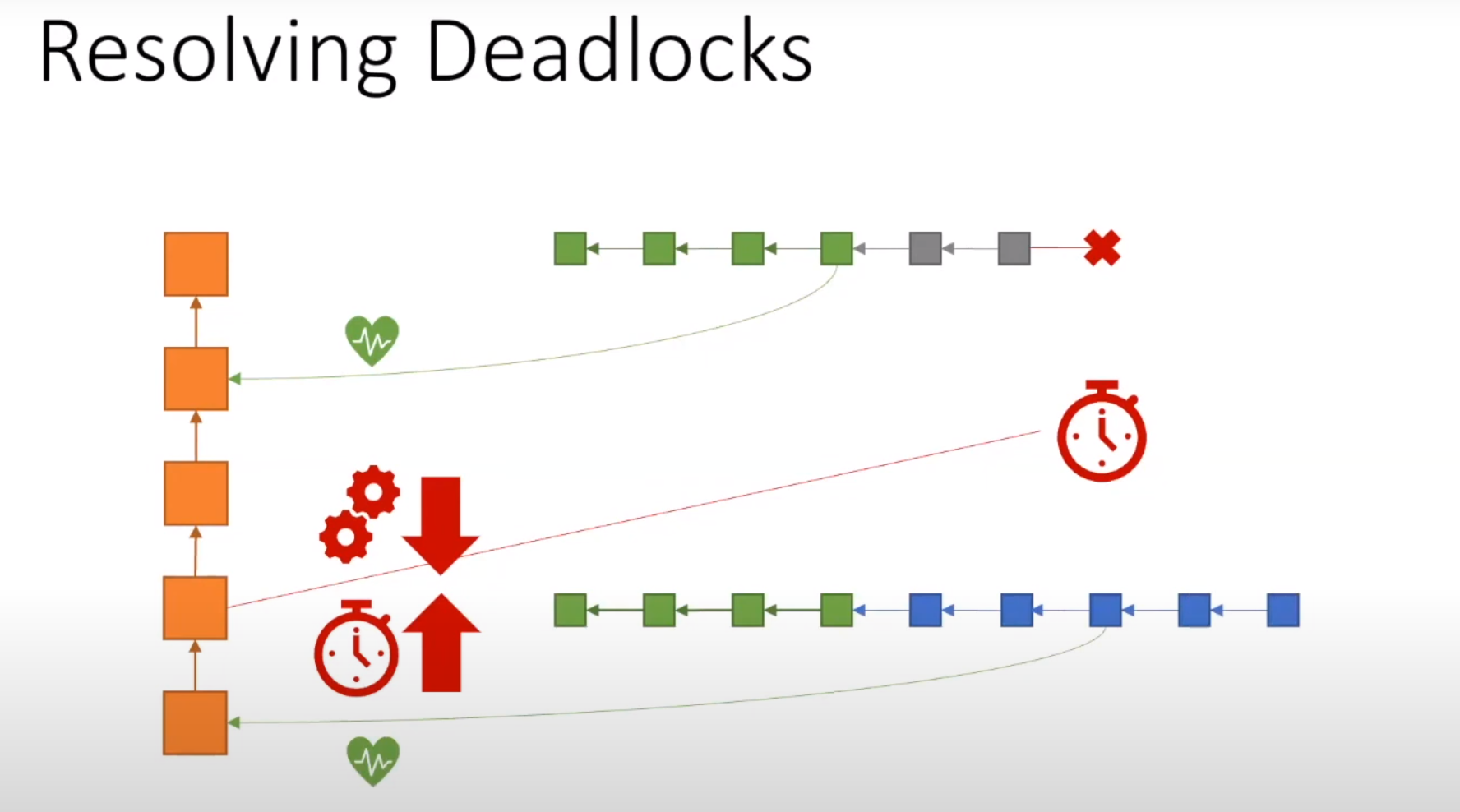
image-20230818193049568

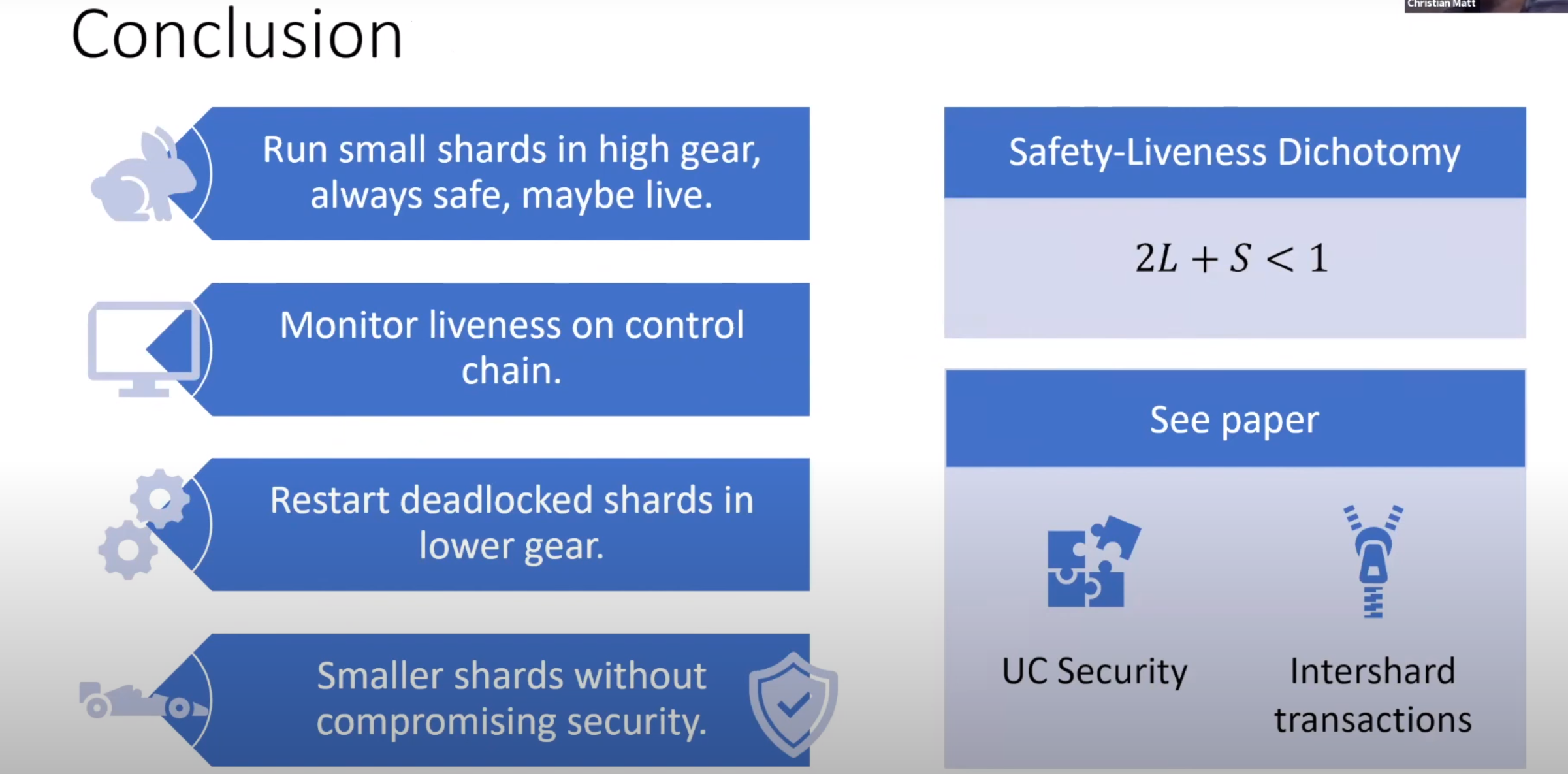
image-20230818193129685

总结

  • 最主要的贡献：给出了将活性和安全性分开的两个不等式
  • 提出了根据具体情况牺牲活性，来提高效率的思想
  • 给出了UC安全的证明（看不懂

可研究的点

  • 目前所有分片都从最低档开始逐级提高活性，能否有其他的机制，一步达到最优的活性的解
    • 首先运行少数分片实例
    • 等待首批分片达到活性后，采用首批分片达到活性时的平均值作为其其余分片的初始配置
  • 本文实际上的分片是要求所有共识节点维护一条全局的链来收集状态，另外分片再维护分片的链进行交易处理
    • Control Chain带来的开销需要考虑
    • 考虑如何优化这种架构
  • 具体如何实现这个共识没有开源