学习南京大学的静态程序分析技术课程
课程主页:Static Program Analysis | Tai-e (pascal-lab.net)
共计32小时
Intro
PL的三个研究方向
- 理论
- 环境
- 应用
- 程序分析
- 静态程序分析
- 程序分析
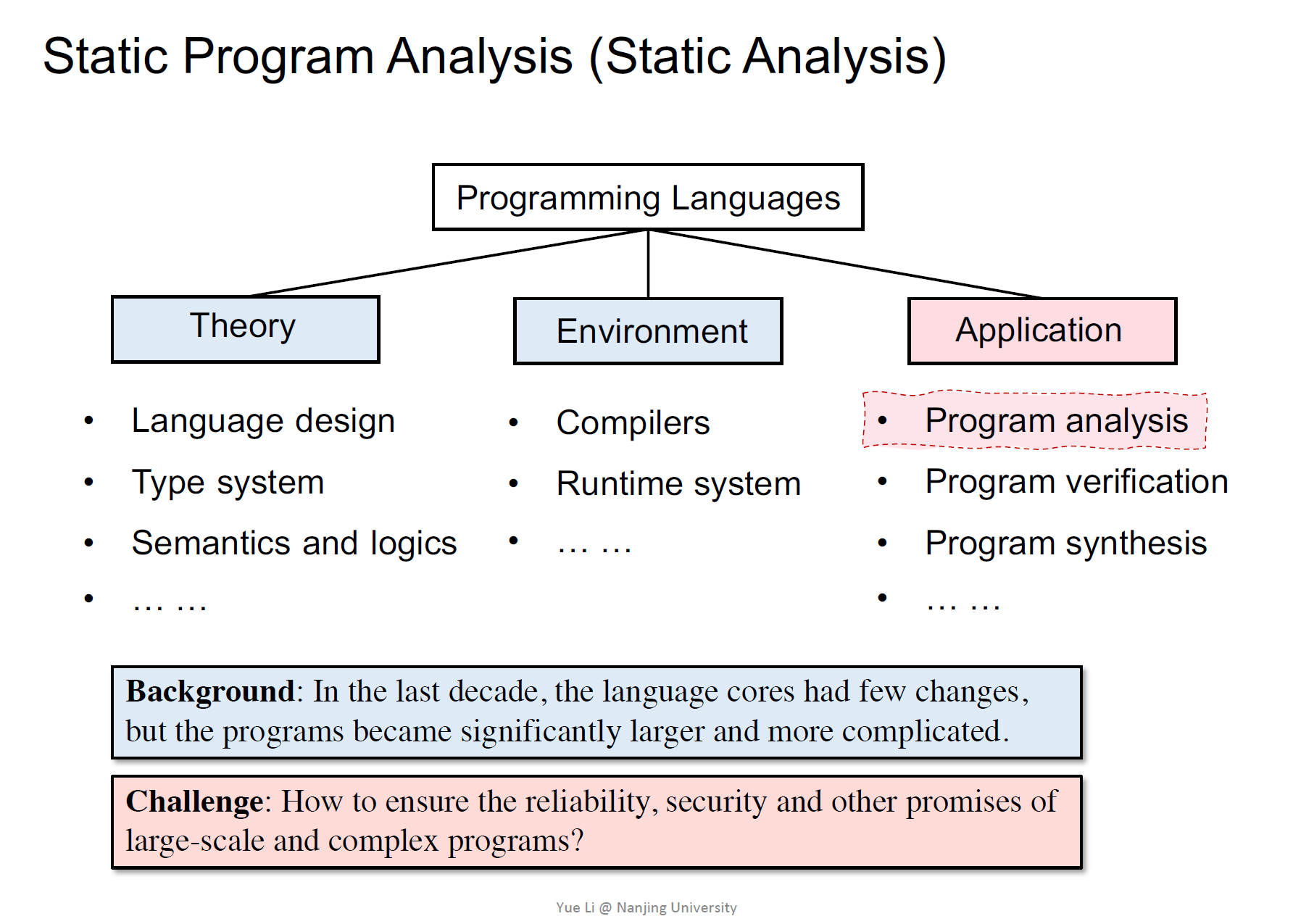
静态分析:在编译时对程序进行检测
静态程序分析的应用
- 程序可靠性
- 安全性
- 编译优化
- O(1)
- 程序理解
- IDE实现的call的提示:利用静态分析实现

运行程序前了解程序的性质和行为(写一个程序来分析,分析器)

- 运行时可能指向同一地址吗
- 需要加锁解决竞争问题

对于一个正常的语言写的程序,我们感兴趣的运行时的性质是否满足 是不可判定的,即不存在完美的静态分析
perfect static analysis满足
- sound:包含所有truth,过近似
- complete:是truth的子集,欠近似
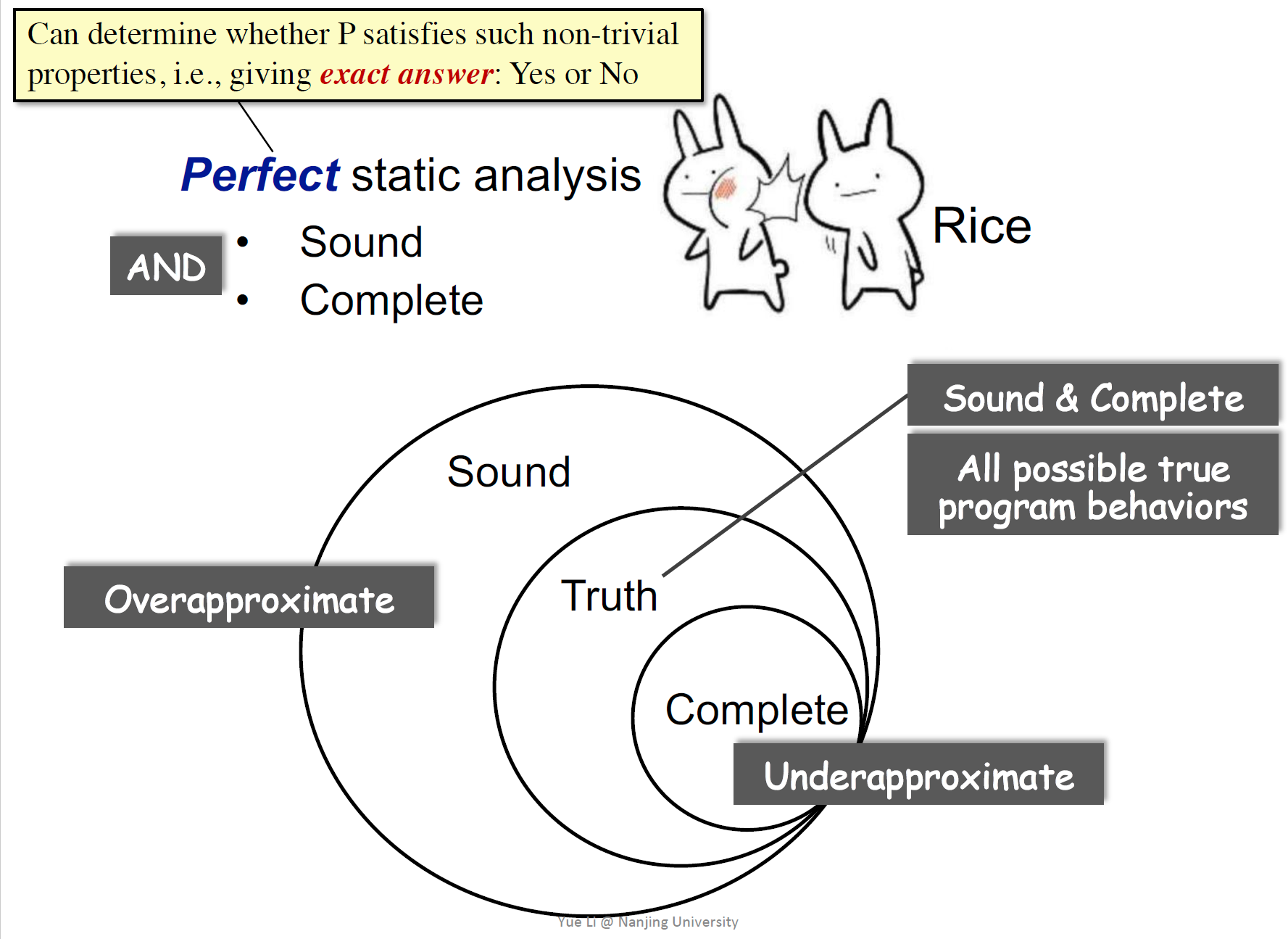
不存在perfect,因此想要一种useful的静态分析,可以仅满足一种性质,妥协另一种性质
- 满足soundness:存在误报,false positive
- 满足complete:存在漏报,false negative
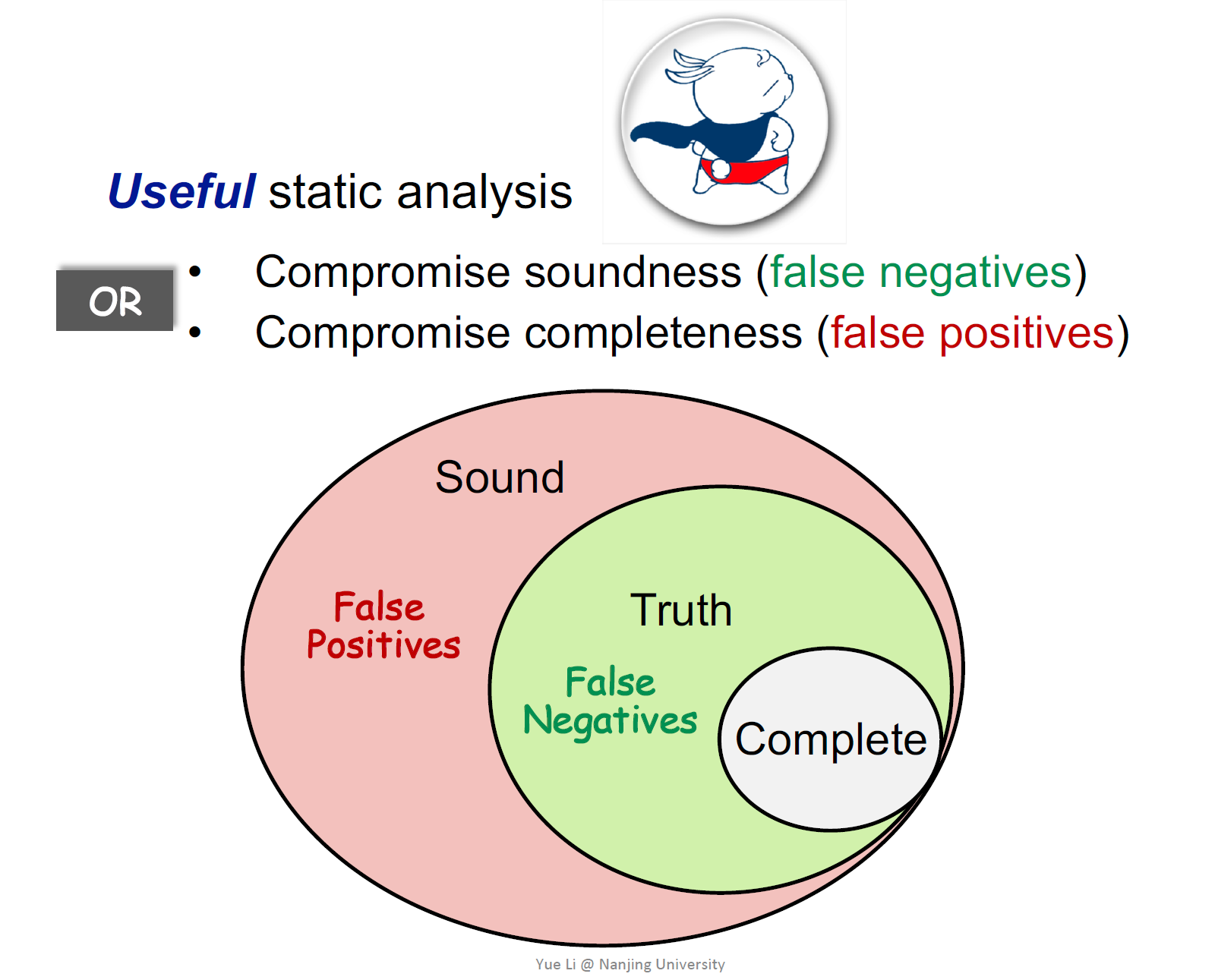
绝大多数的程序分析都是sound,妥协complete
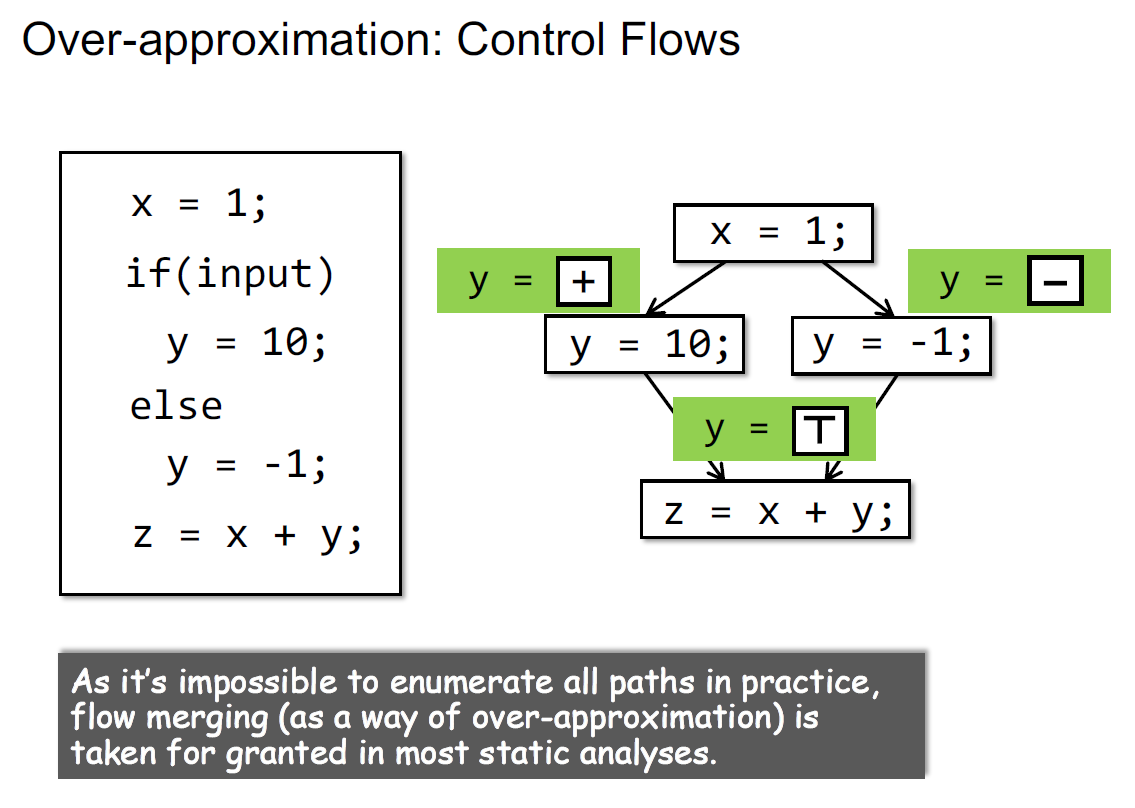
sound一般对应的是正确性,如下例,考虑到两条分支后才能得出正确的结论
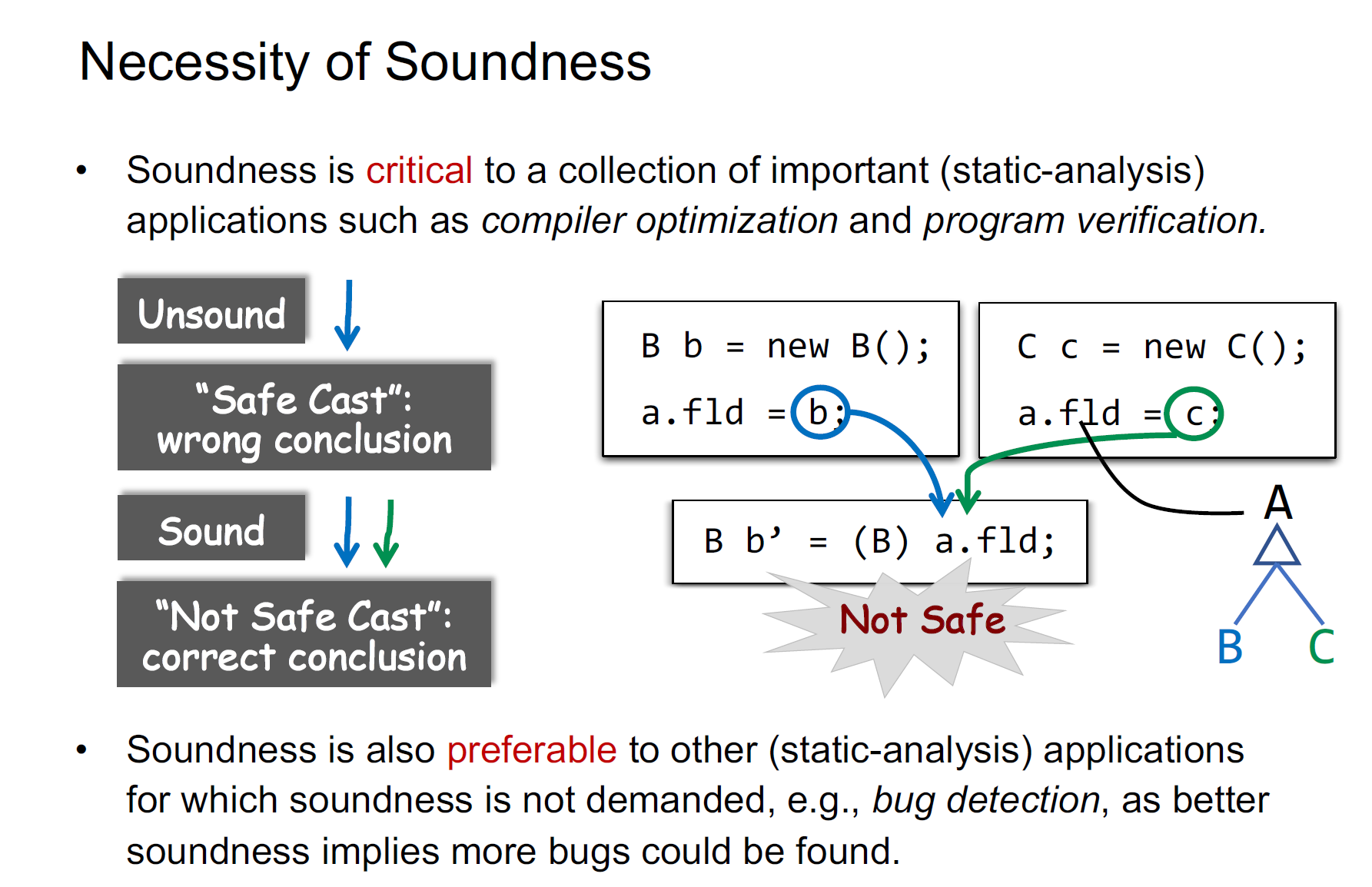
可能有两个结论,都是sound的
平常的思维是动态思维,静态分析无法获得运行时的数据
第一个结论需要维护path branch和一个条件,比较昂贵;第二个比较cheap,速度快
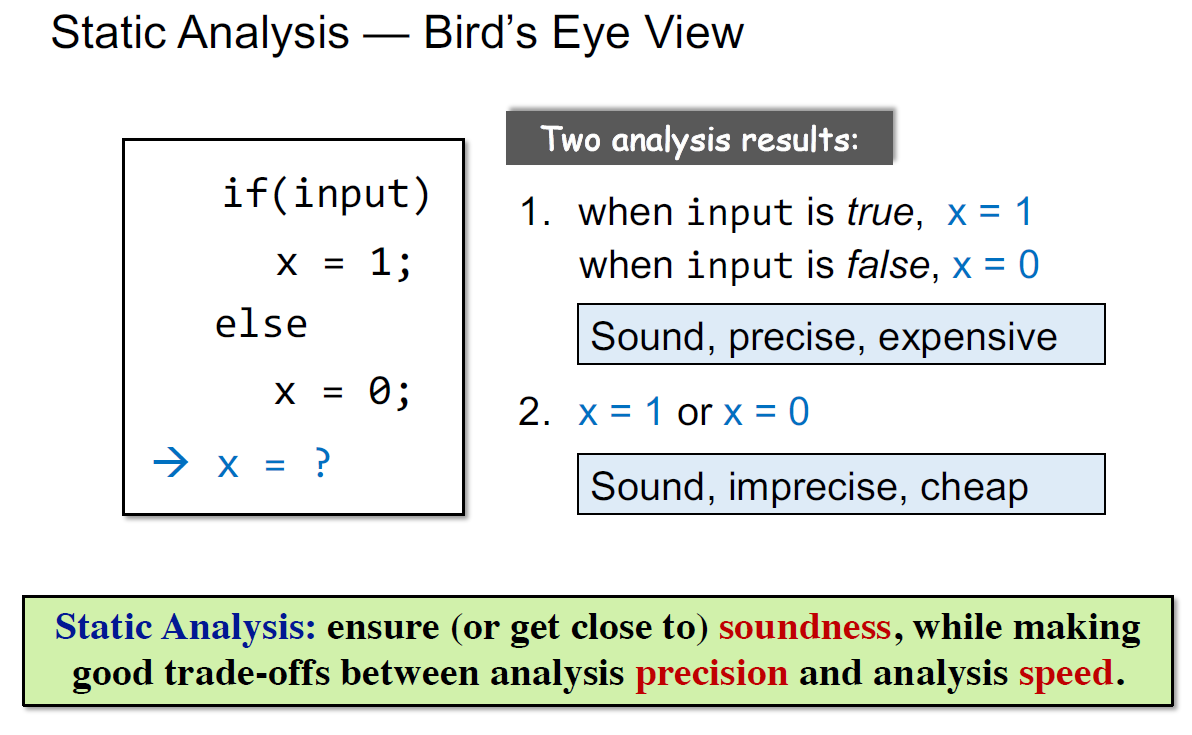
确保(足够接近)soundness的情况下,在精度和分析速度上做平衡
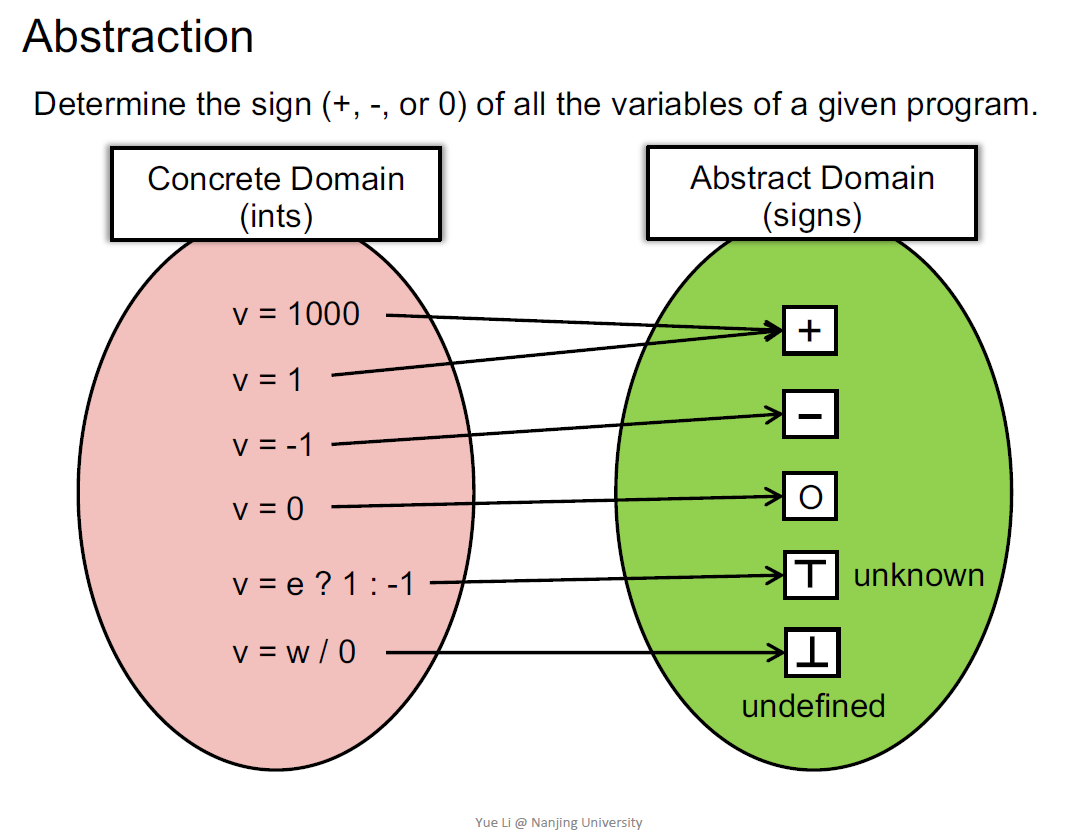
抽象 过近似 是静态分析的核心思想
过近似包括transfer函数和控制流
抽象就是把具体值转变为符号
用bottom符号表示错误
transfer functions定义了转换规则,根据分析的具体问题和语句的语义设计
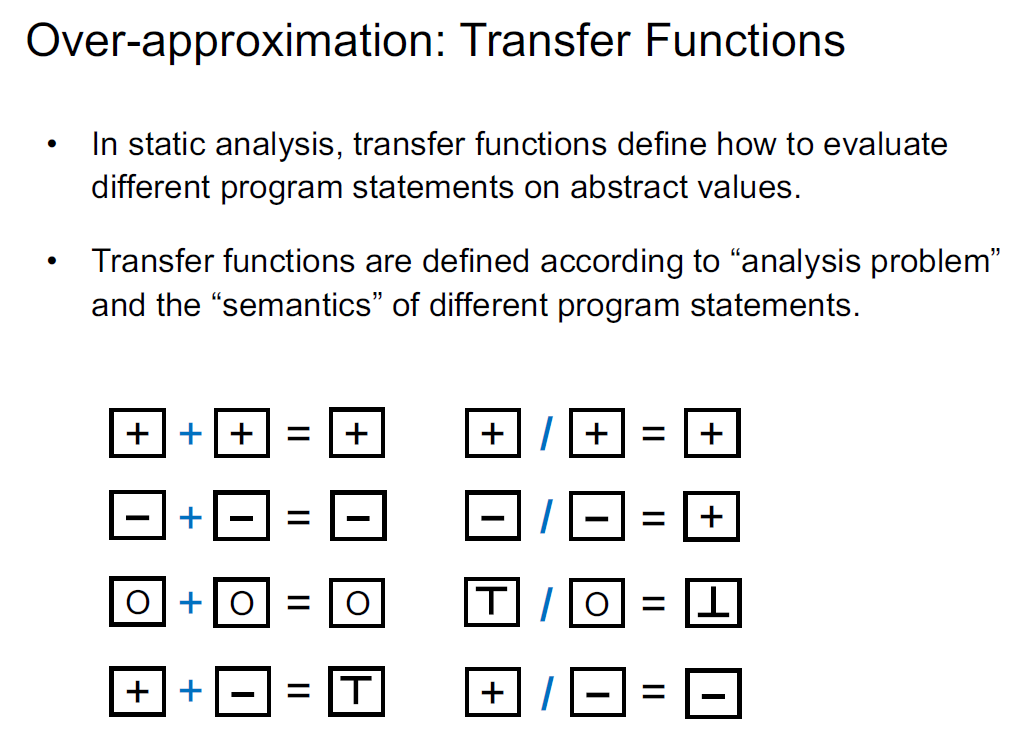
3说明静态分析会产生误报
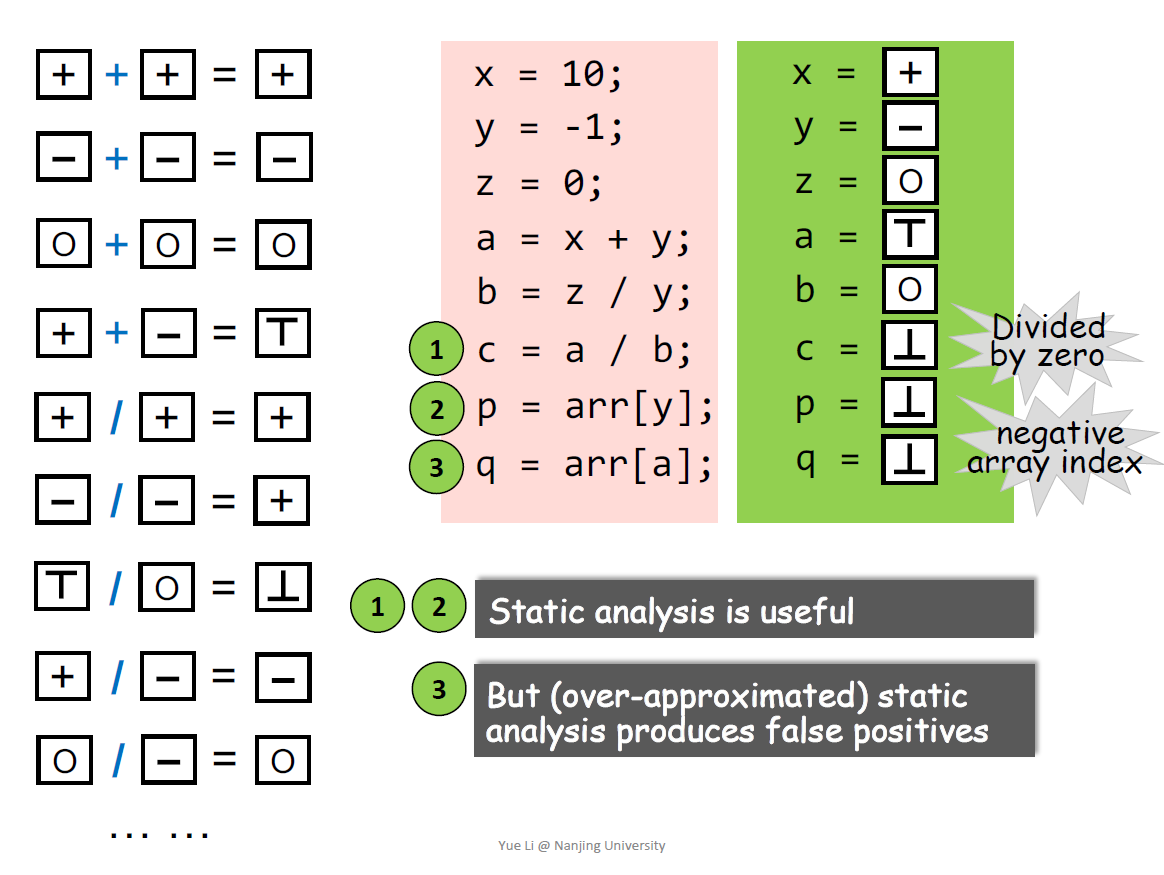
控制流:在每个merge的地方进行抽象,可能出现过近似,默认采用的方式

Intermediate Representation
南京大学《软件分析》课程02(Intermediate Representation)_哔哩哔哩_bilibili
直接分析源代码存在弊端
静态分析需要一种程序表示的形式,没有严格的定义,因此介绍主流的IR
不介绍对C/C++的LLVM
编译器和静态分析器
了解关系即可
编译的步骤:
词法分析(符号和词的合法性),需要词法方法,正则表达式
- 语法分析器parser,上下文无关文法
语法分析,对AST进行分析,语义指简单的(类型检查)
- 代码生成,静态分析器在IR基础上做
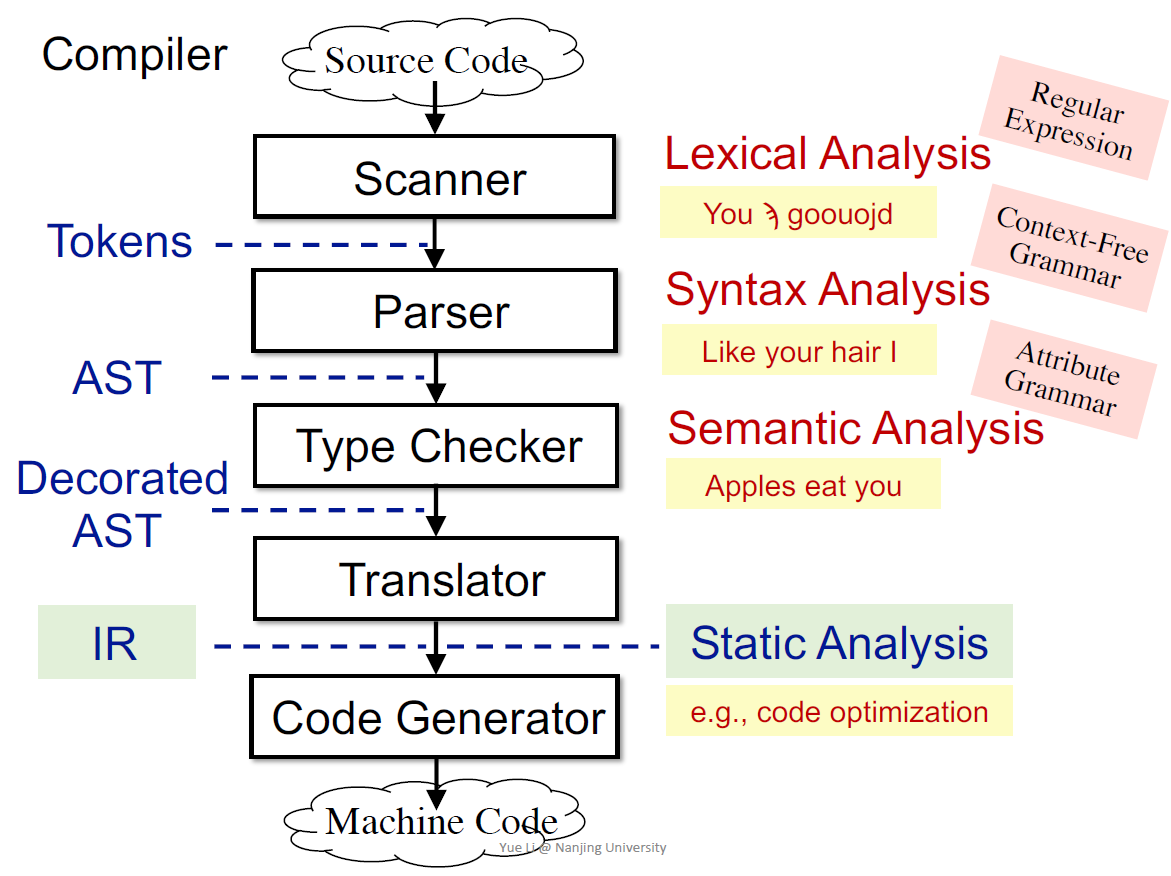
正常的IR需要所有前端模块才能生成
AST vs. IR
3地址码3-address code
IR更接近于机器码,不依赖于编程语言(方舟编译器可以将不同语言生成为统一的IR)
AST缺乏对控制流的表达
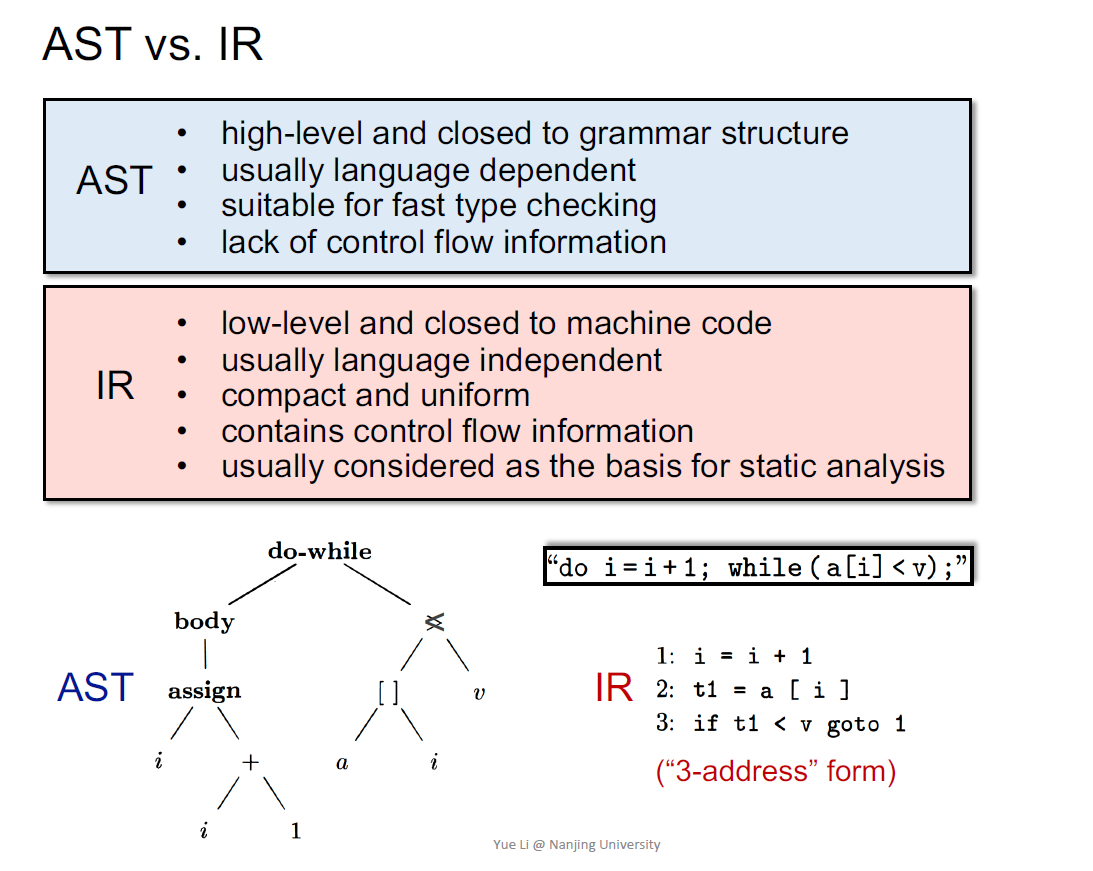
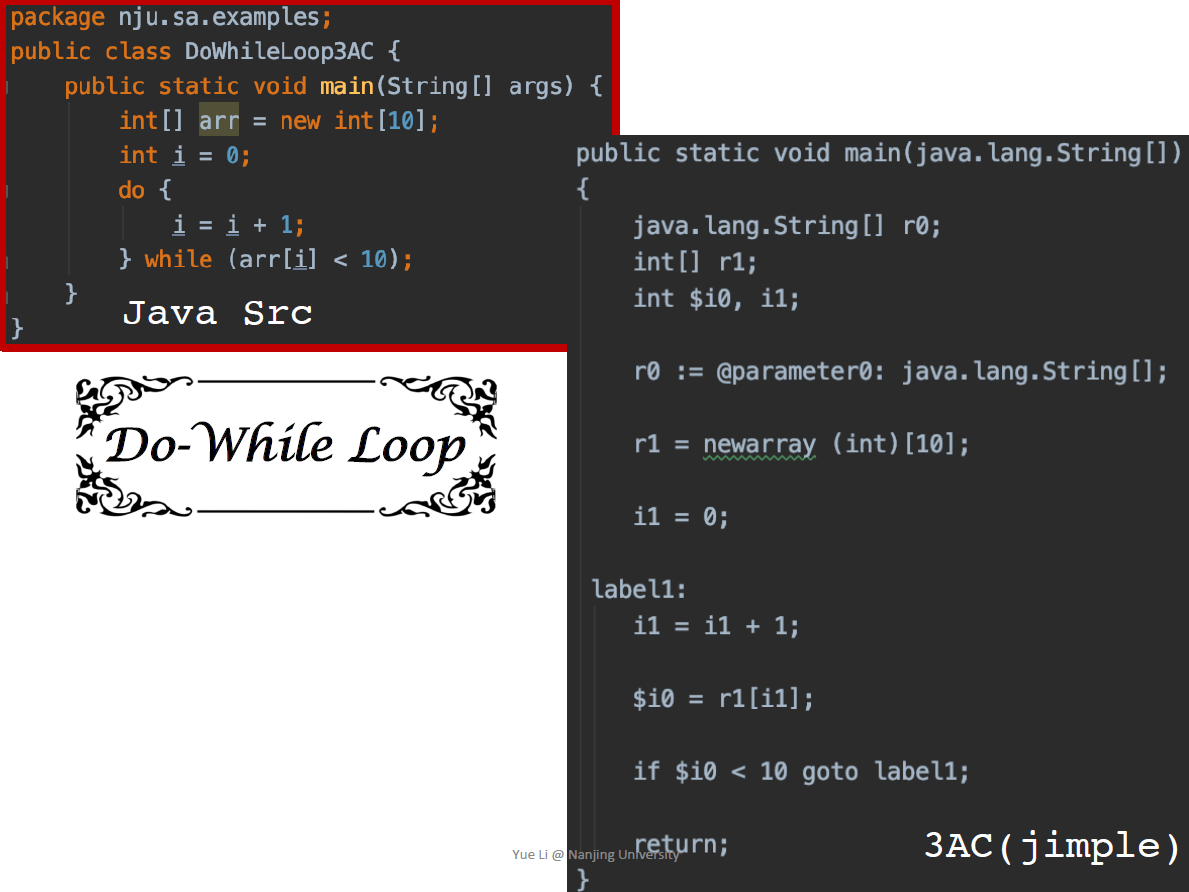
IR: 3AC
没有形式化的定义

指令右端只有1个操作符,每个语句只包含3个地址
- 变量名 a,b
- 常量 3
- 编译器自动生成的临时变量 t1
常见的形式

Soot
java中最流行的静态分析器
https://github.com/Sable/soot/wiki/Tutorials
对应的IR是 Jimple,带有类型的3地址码
冒号是一种特殊的赋值
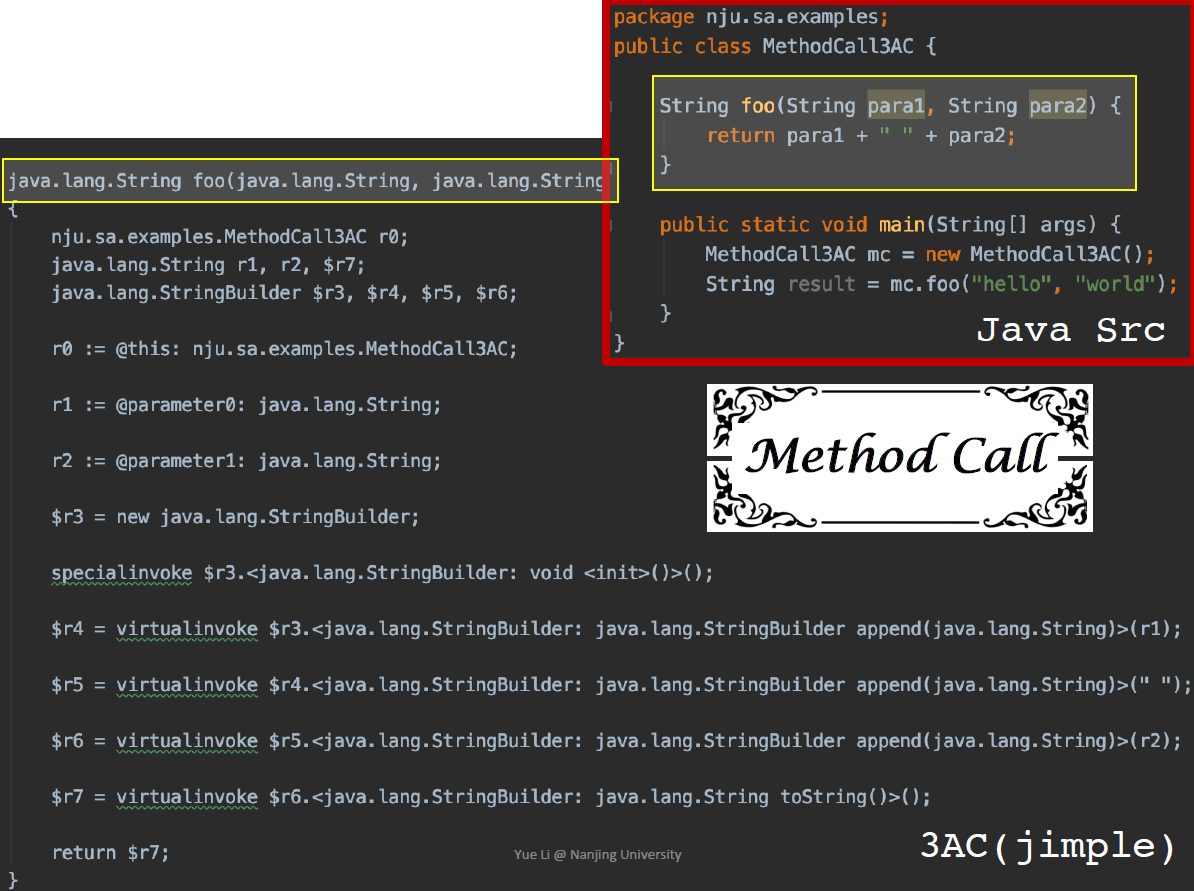
JVM中的4种调用
invokespecial: call constructor, call superclass methods, call private methods
invokevirtual: instance method call (virtual dispatch)
invokeinterface: cannot optimization, checking interface implementation 不能优化
invokestatic: call static methods
Java7 invokedynamic -> Jaava static typing, dynamic runs on JVM
meethod signature: class name, return type, method name, parameter types
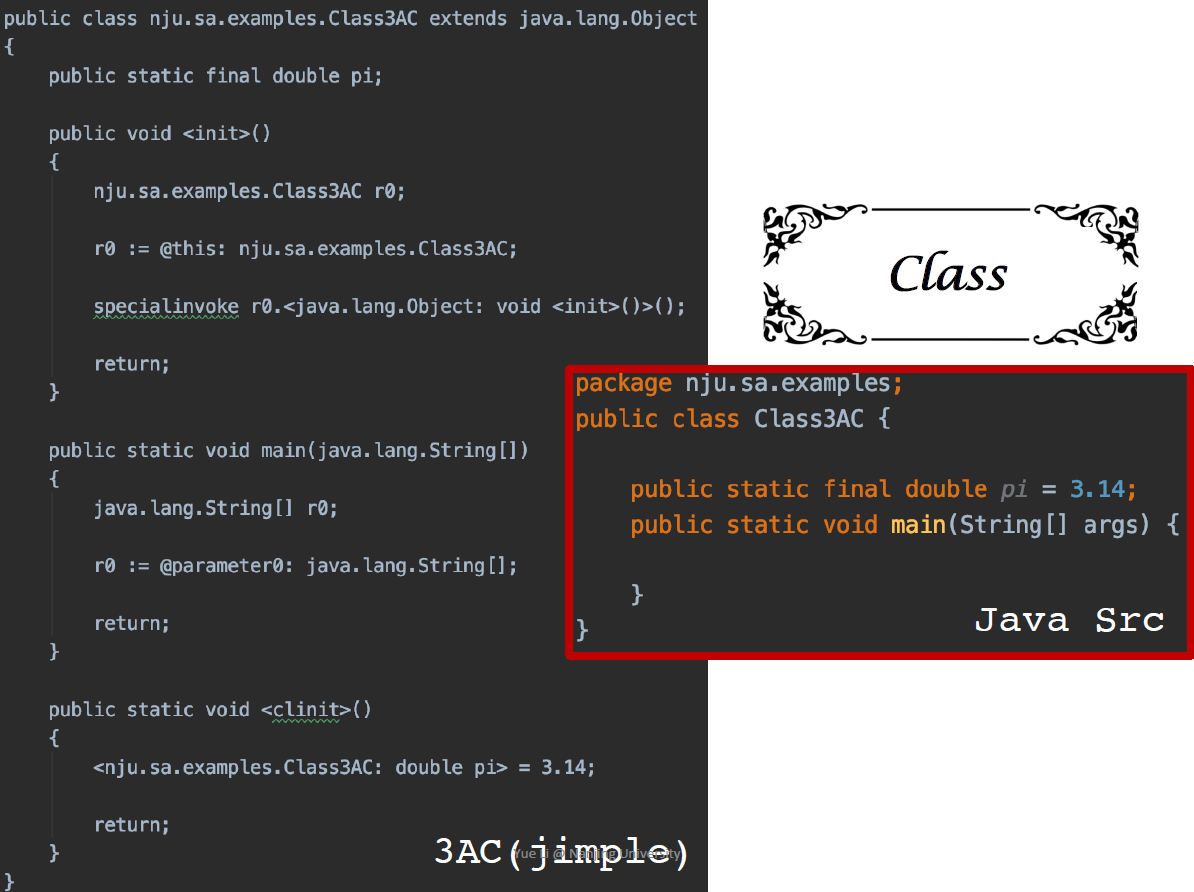
所有类的父类,java.lang.object
默认生成的构造函数init
clinit 类的初始化的函数,compiler加载引用的变量进行初始化 class load init
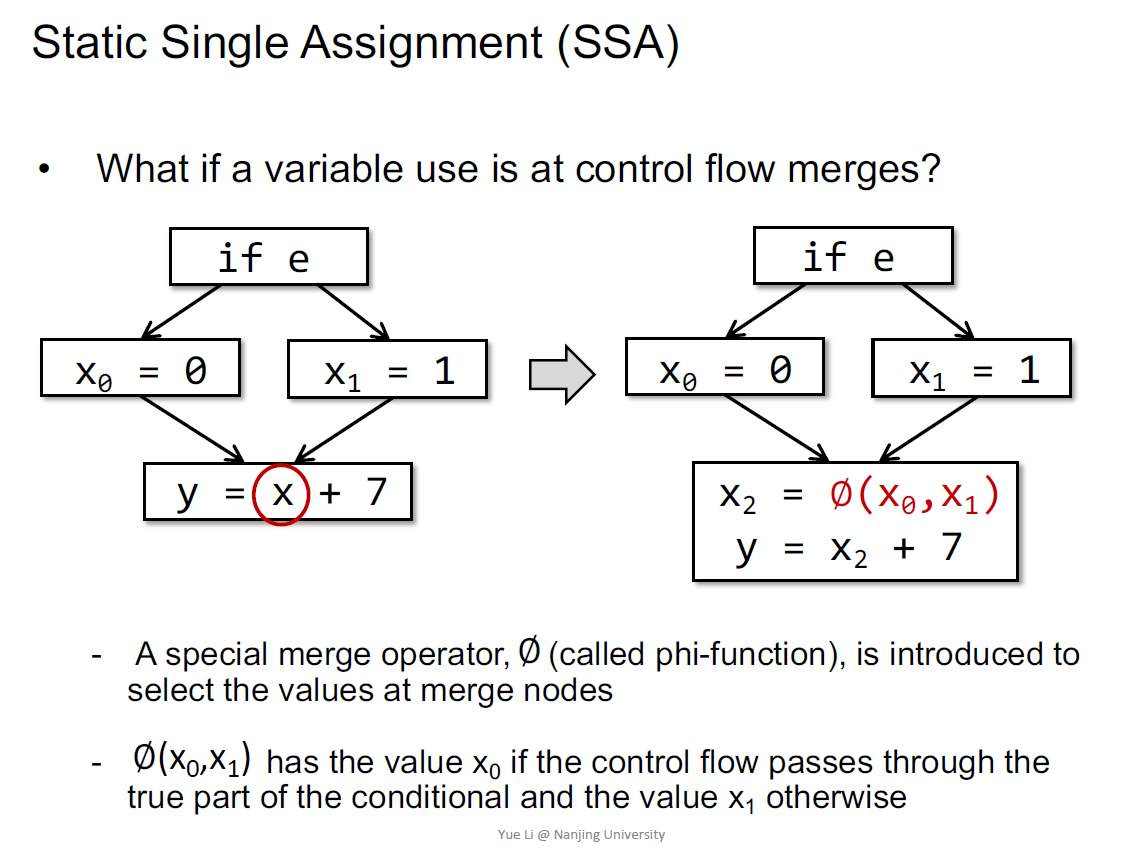
SSA
一种IR,有利于某些算法的设计,80年代提出的技术
和3AC的区别是每个变量的定义有新的命名,每个变量仅有一个等式

如果有控制流,采用$\phi$函数
为什么使用SSA
flow-sensitive 维护程序执行顺序,精度更高,SSA本身带有部分flow的信息
数据的存储更清晰
为什么不用SSA
- 引入变量太多
- 译为机器码可能开销太大

静态分析一般在CFG上分析,如何给定3AC建立CFG?
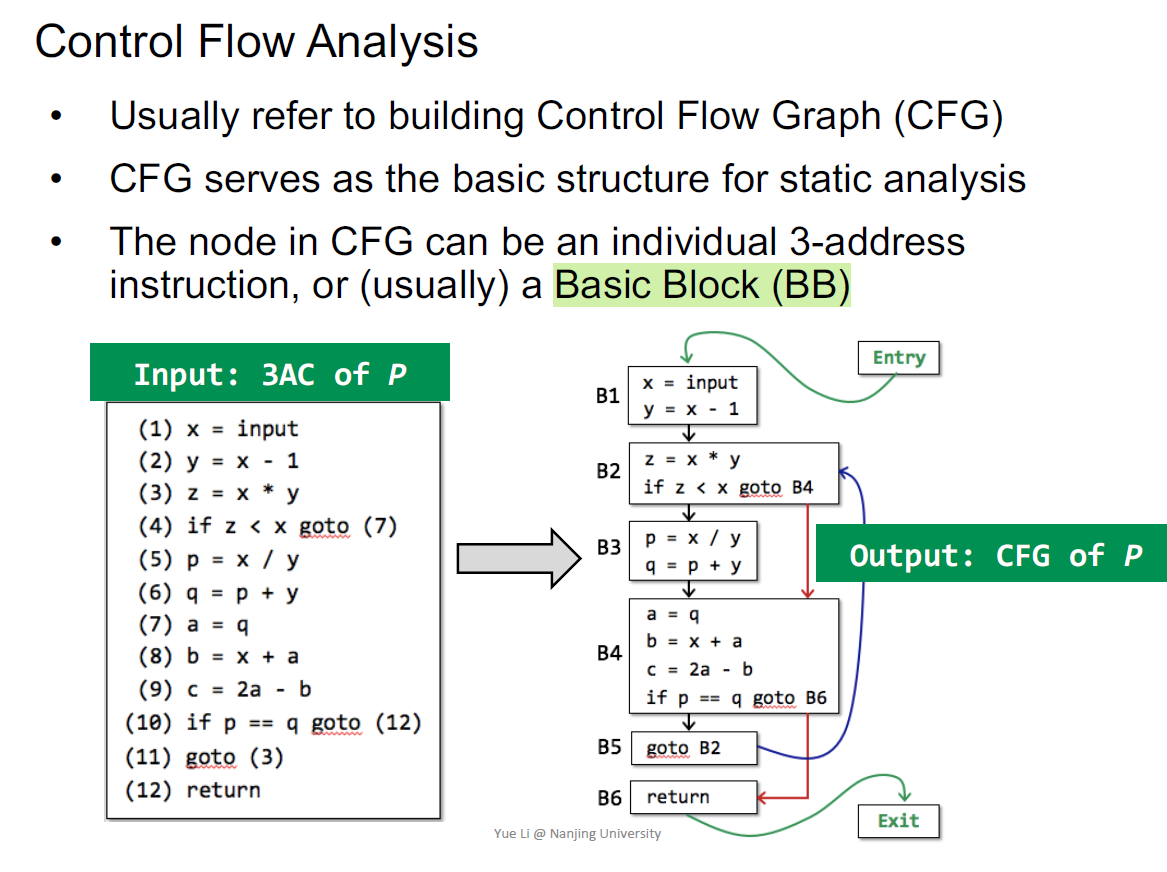
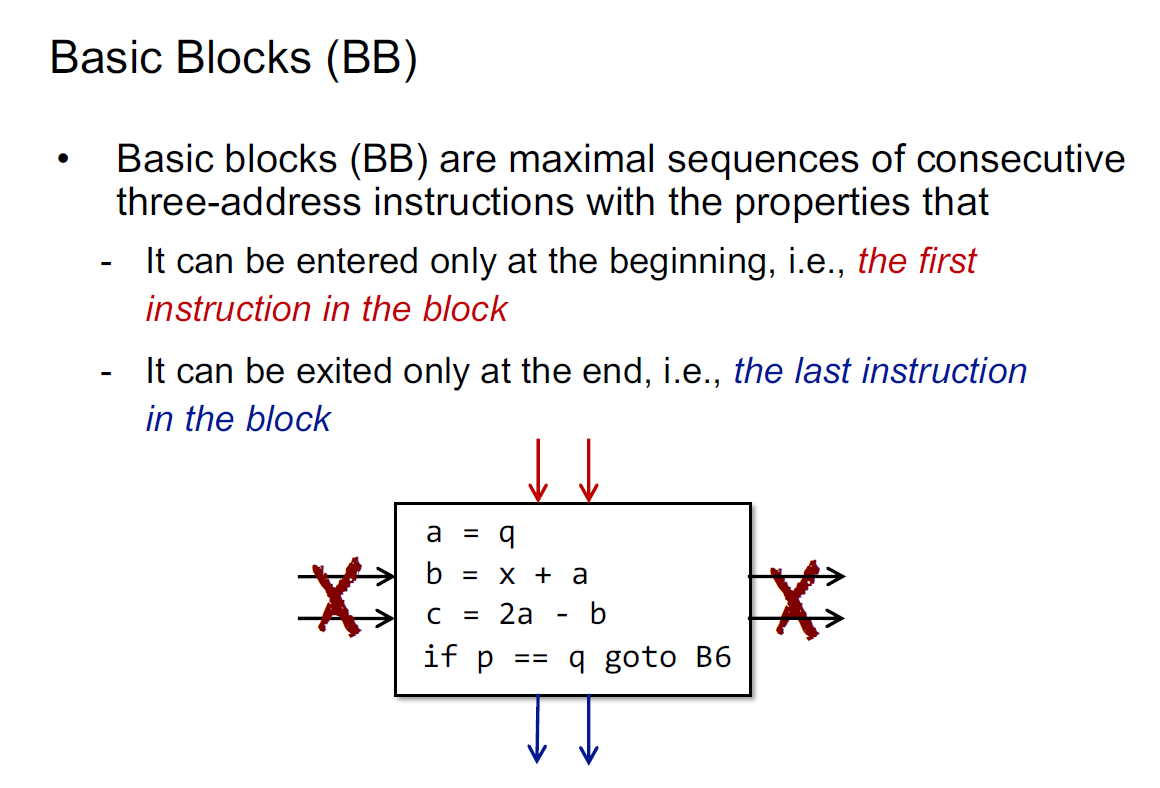
Basic Blocks
basic blocks是最多的连续的3AC码的集合,满足以下指令:
- 只能从第一个指令进入(没有其他控制流
- 出口是最后一个指令
- 如果指令是goto的地址,只能作为入口
- goto只能作为出口
- goto的下一句一定是入口

仅确定入口即可
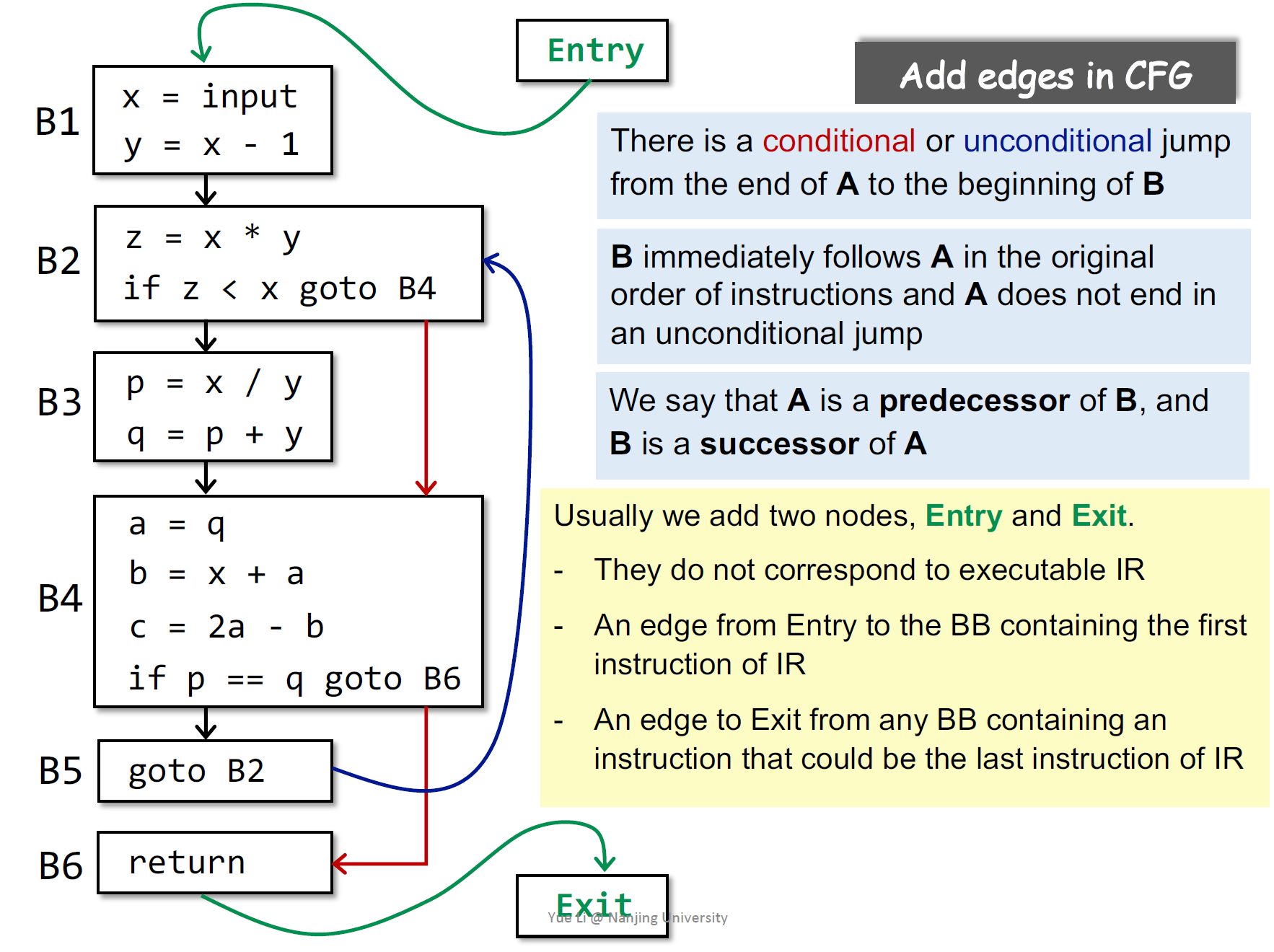
BB是CFG的节点,补充边就有了CFG

CFG
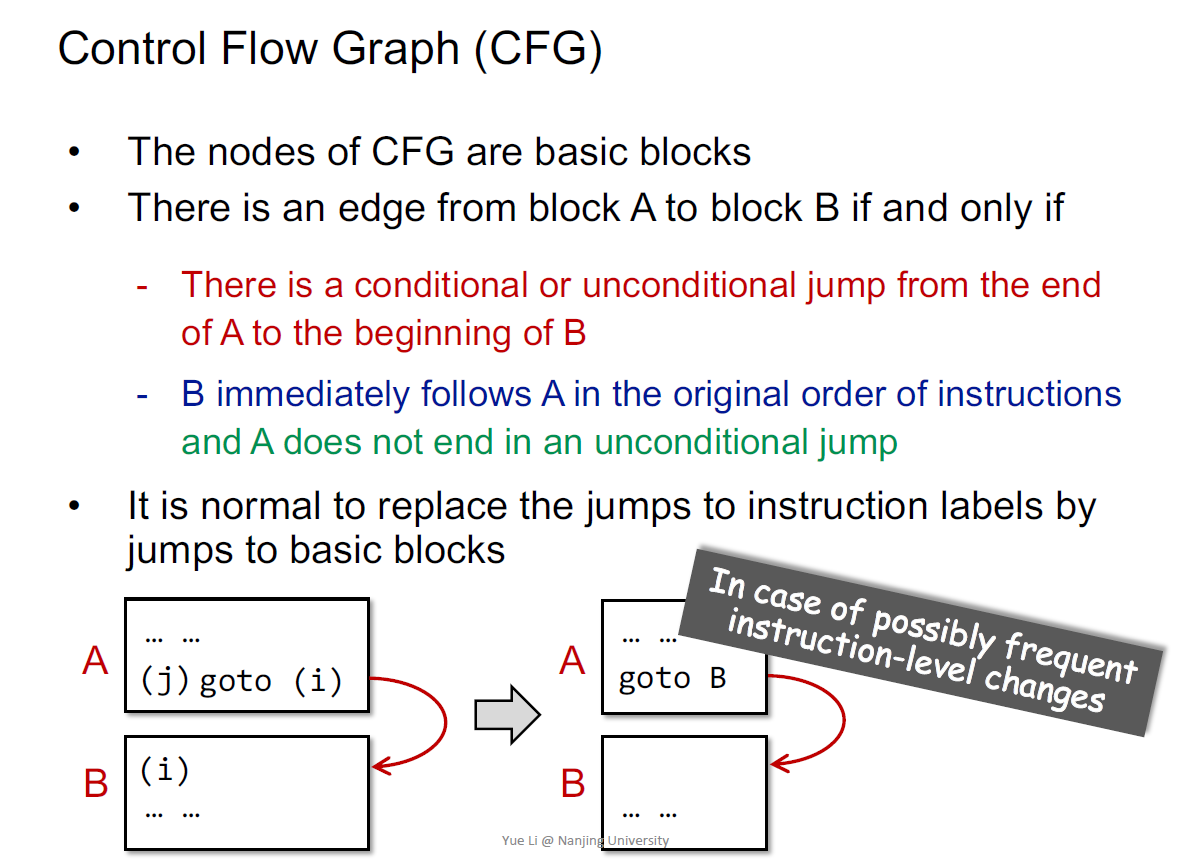
条件jump有2两个出口
B2是B1的后继,前驱只能有一个,后继可以有多个
entry也可以有很多

IR和AST的区别

企业可能认为content-insentive比较慢,学术界关注的是content-sensitive的技术
Data Flow Analysis Applications
编译后端优化的技术
3个应用

Overview of Data Flow Analysis
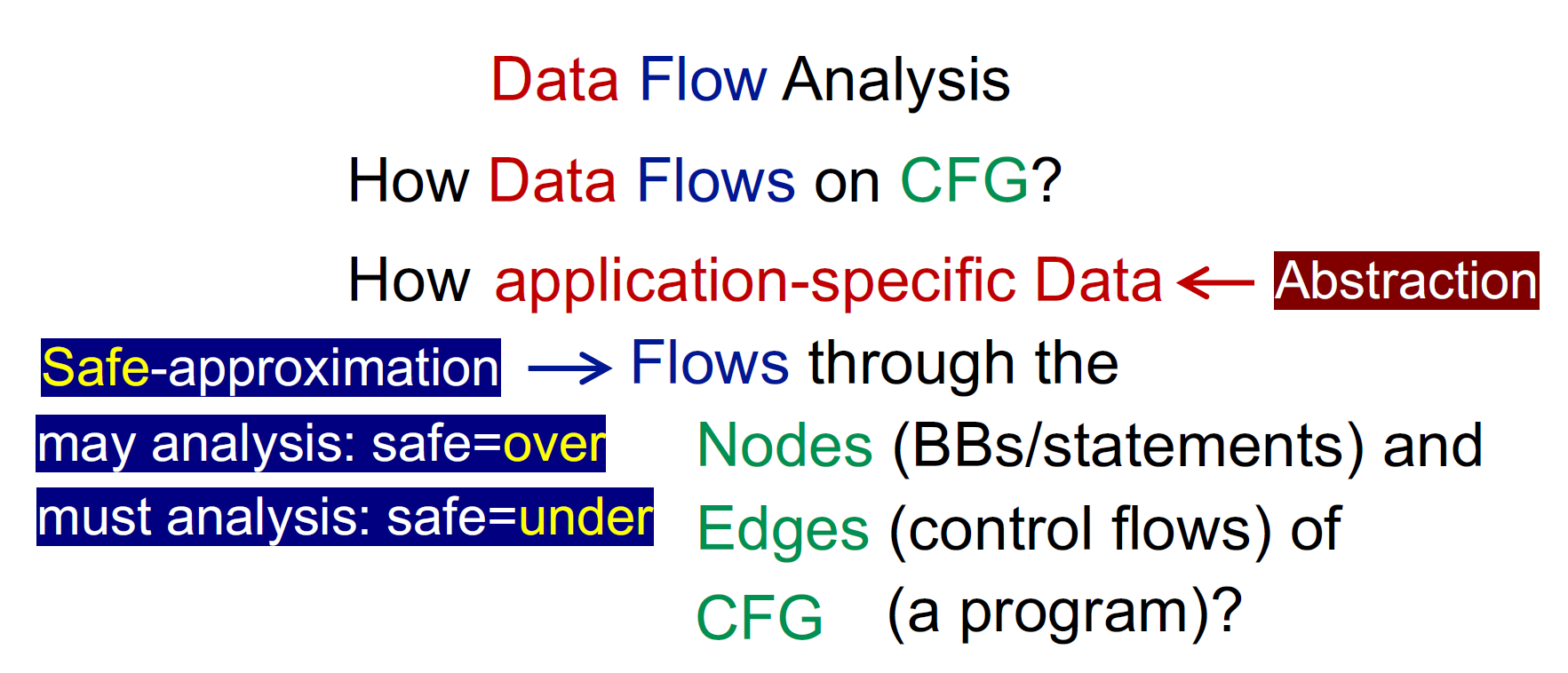
研究数据怎样在CFG中流动
静态程序分析是过拟合的,输出可能是假阳

过拟合和欠拟合都是安全的分析,应该将over改成safe
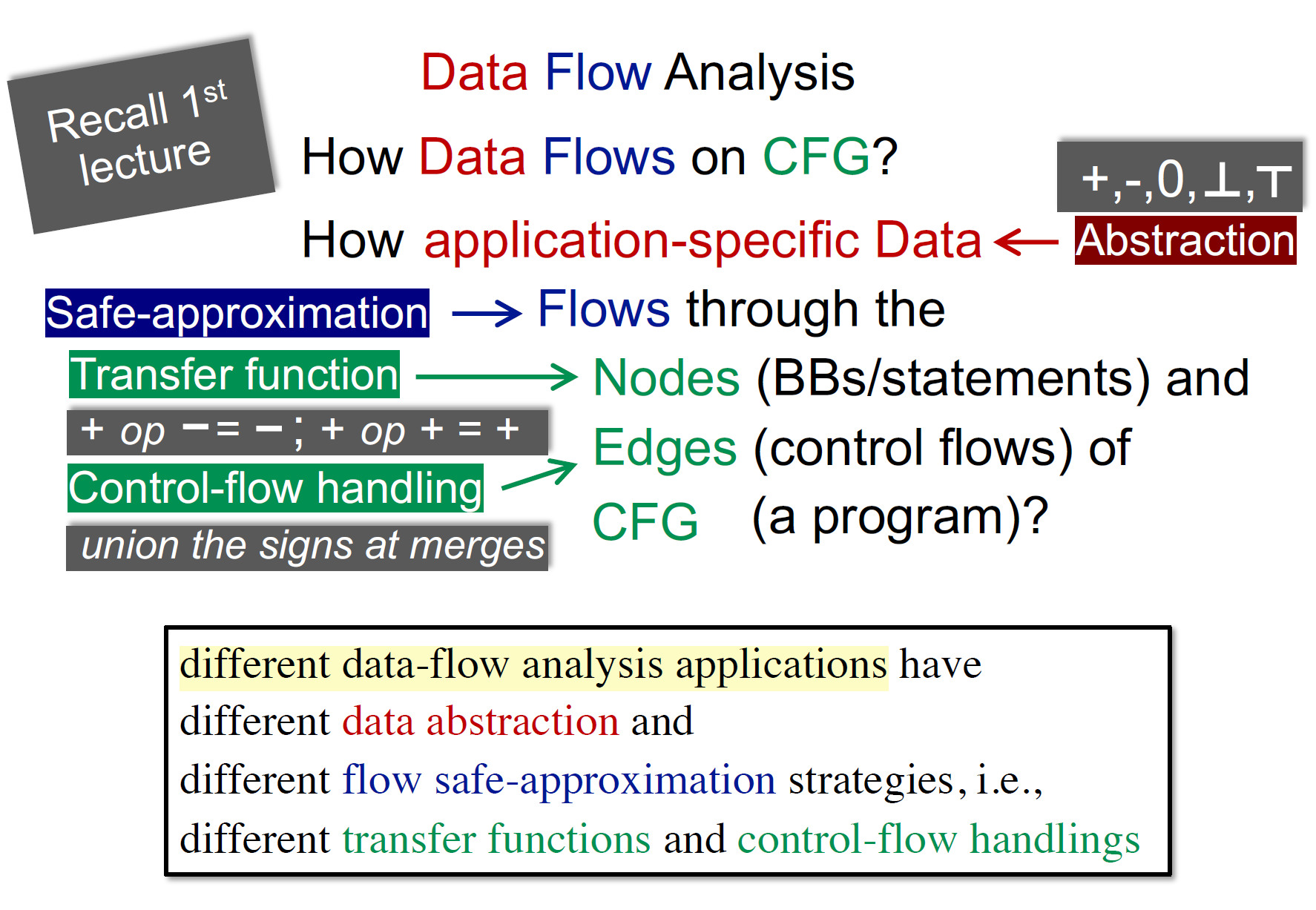
主要介绍不同的数据流分析的应用
Preliminaries of Data Flow Analysis
形式化方法
程序执行前后会产生状态变化,与程序点关联
顺序执行的语句前一条语句的输出和后一条的输入相关,具体还有分支的形式
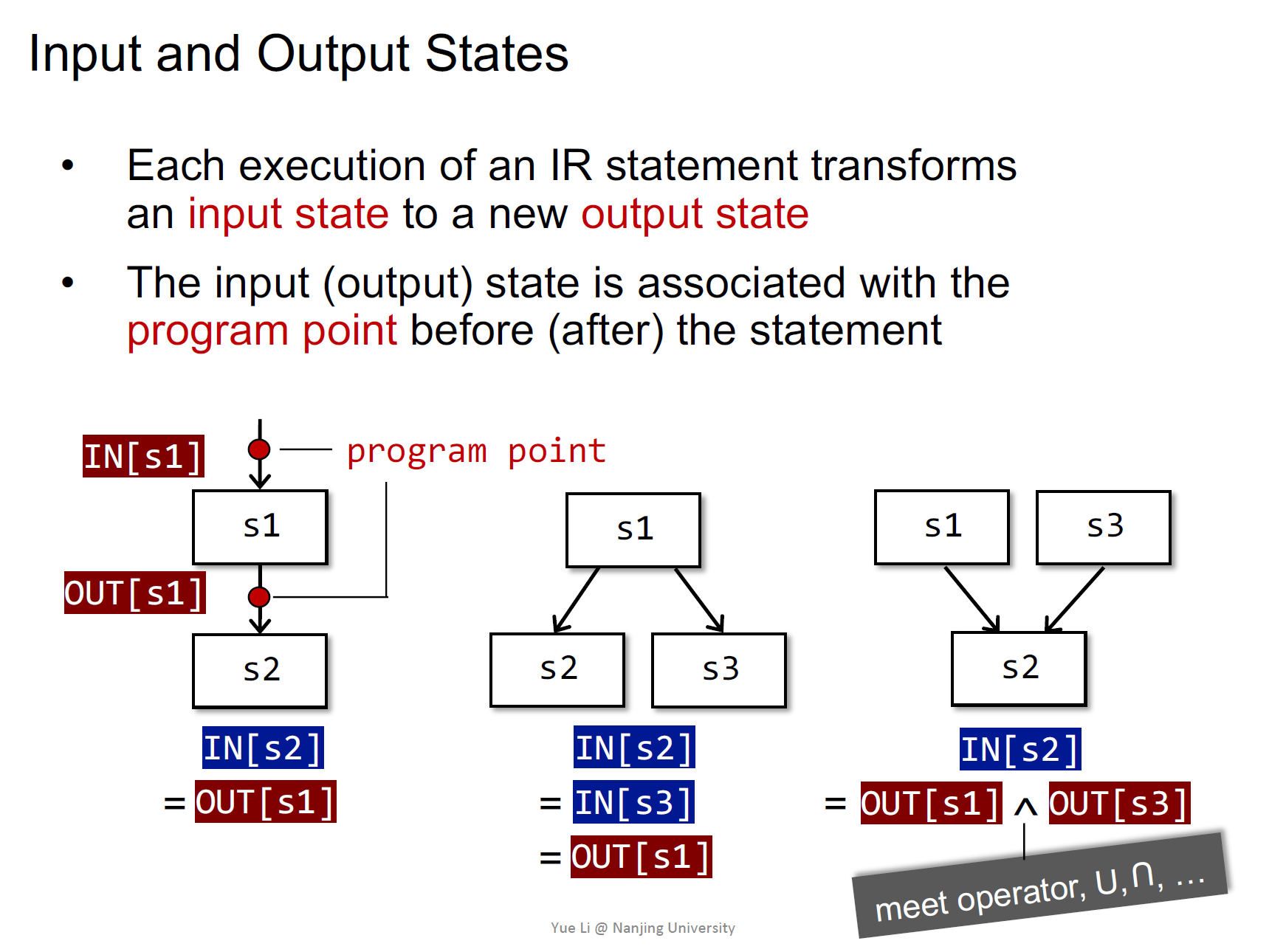
操作符是meet operator,可以是union或者其他运算符
数据流分析需要对每个程序点的所有可能状态的抽象(data flow value,绿色的)
domain是value的值域
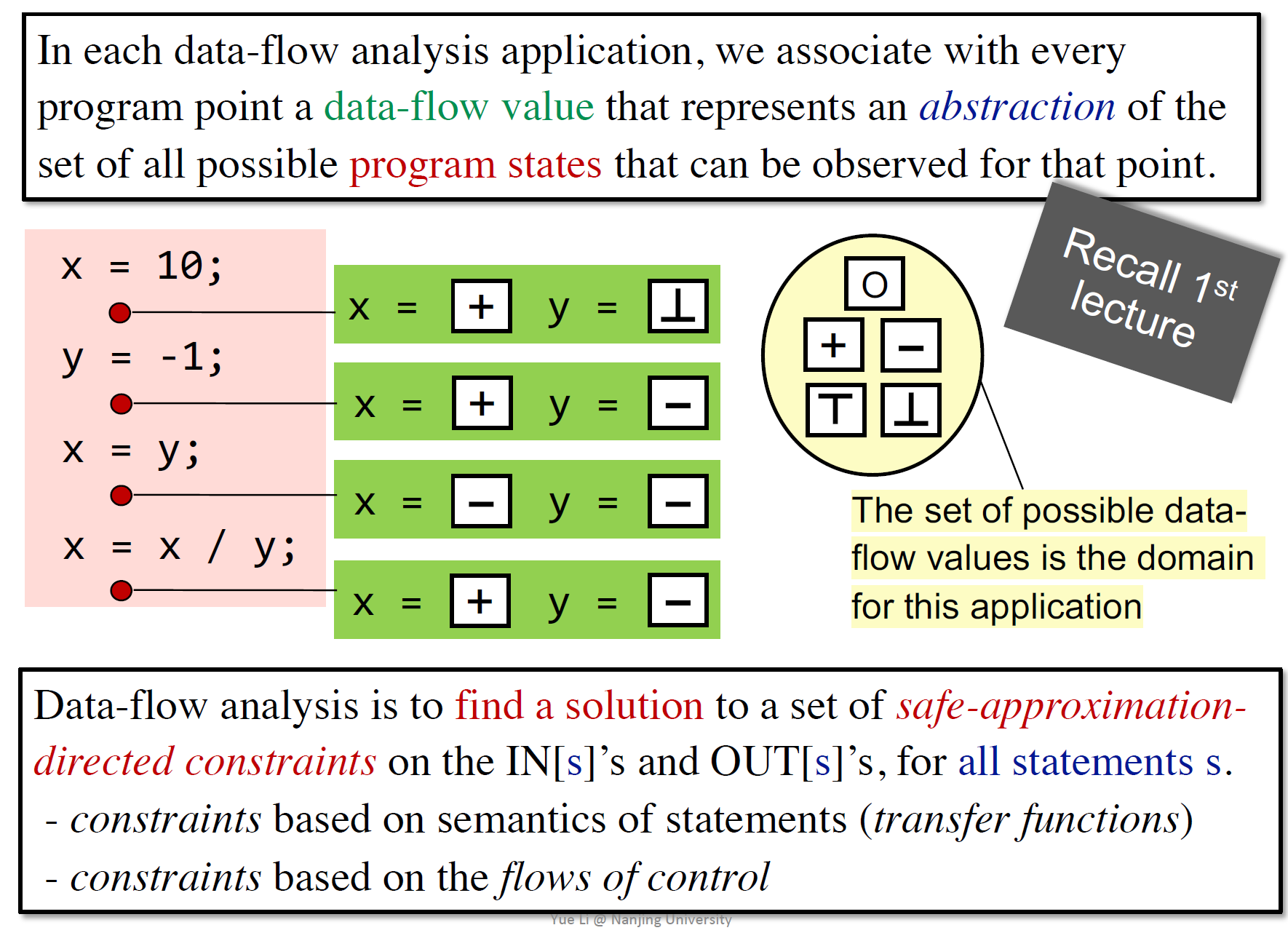
数据流分析是为了找到对输入输出状态的约束的解,有两类
- 基于状态的语义(转移函数)
- 前向分析
- 反向分析(可能会对逆向的CFG进行前向分析)
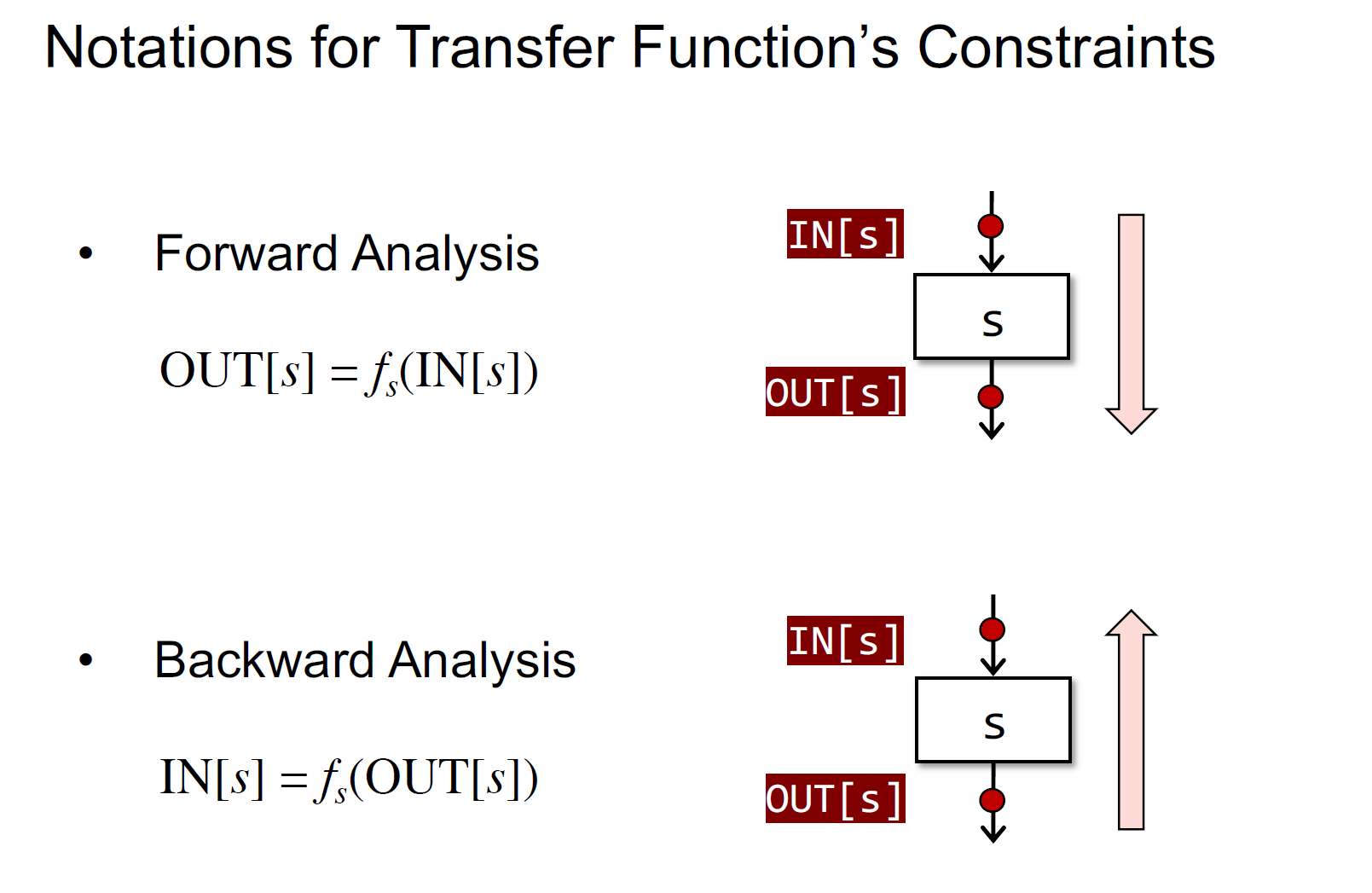
- 基于控制流的约束
- Basic Blocks里面的
- $IN[s_{i+1}]=OUT[s_i],\text{for all }i\in\{1,\dots,n-1\}$
- BB之间的
- 复合函数
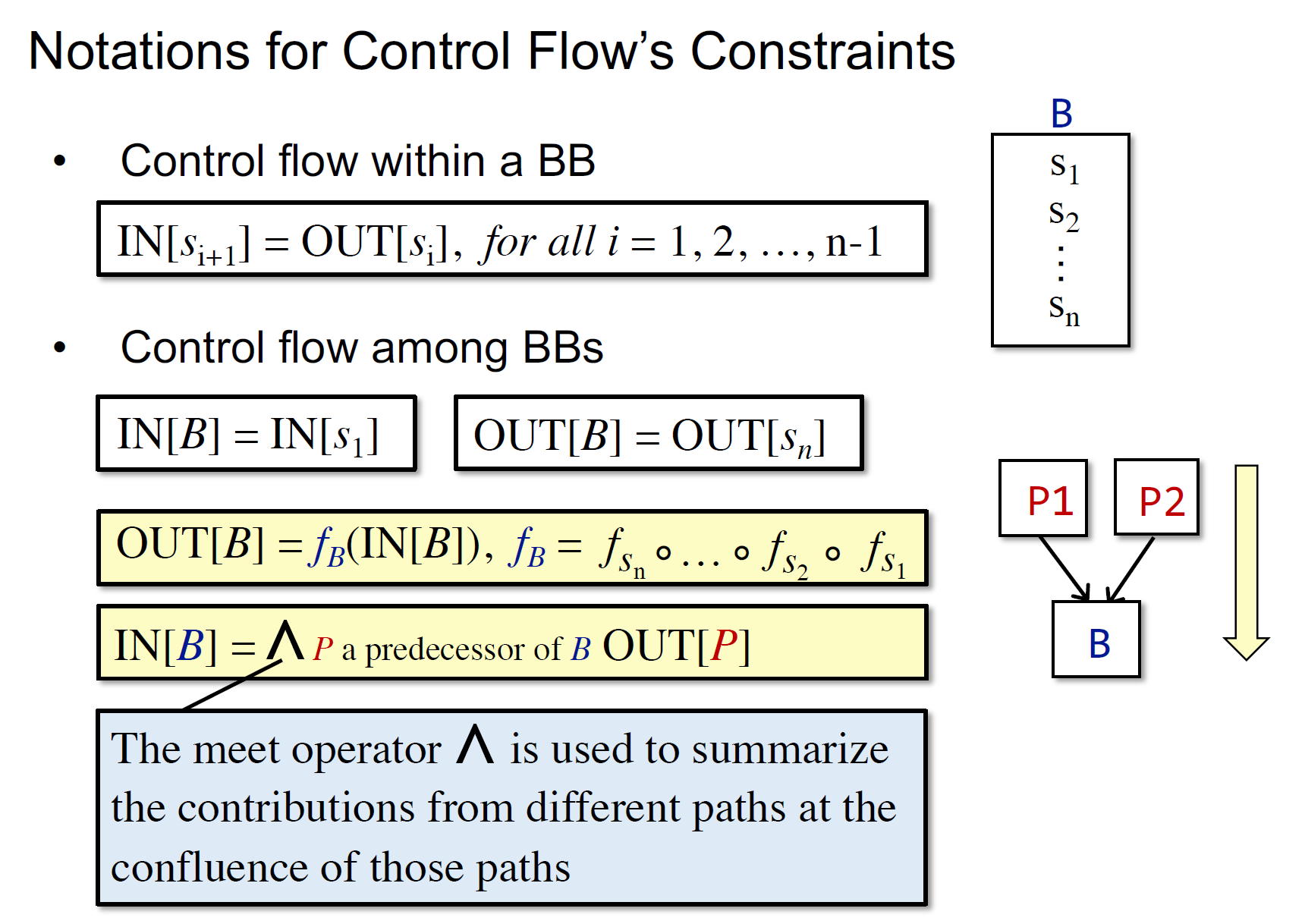

- 红色的是反向的
- Basic Blocks里面的
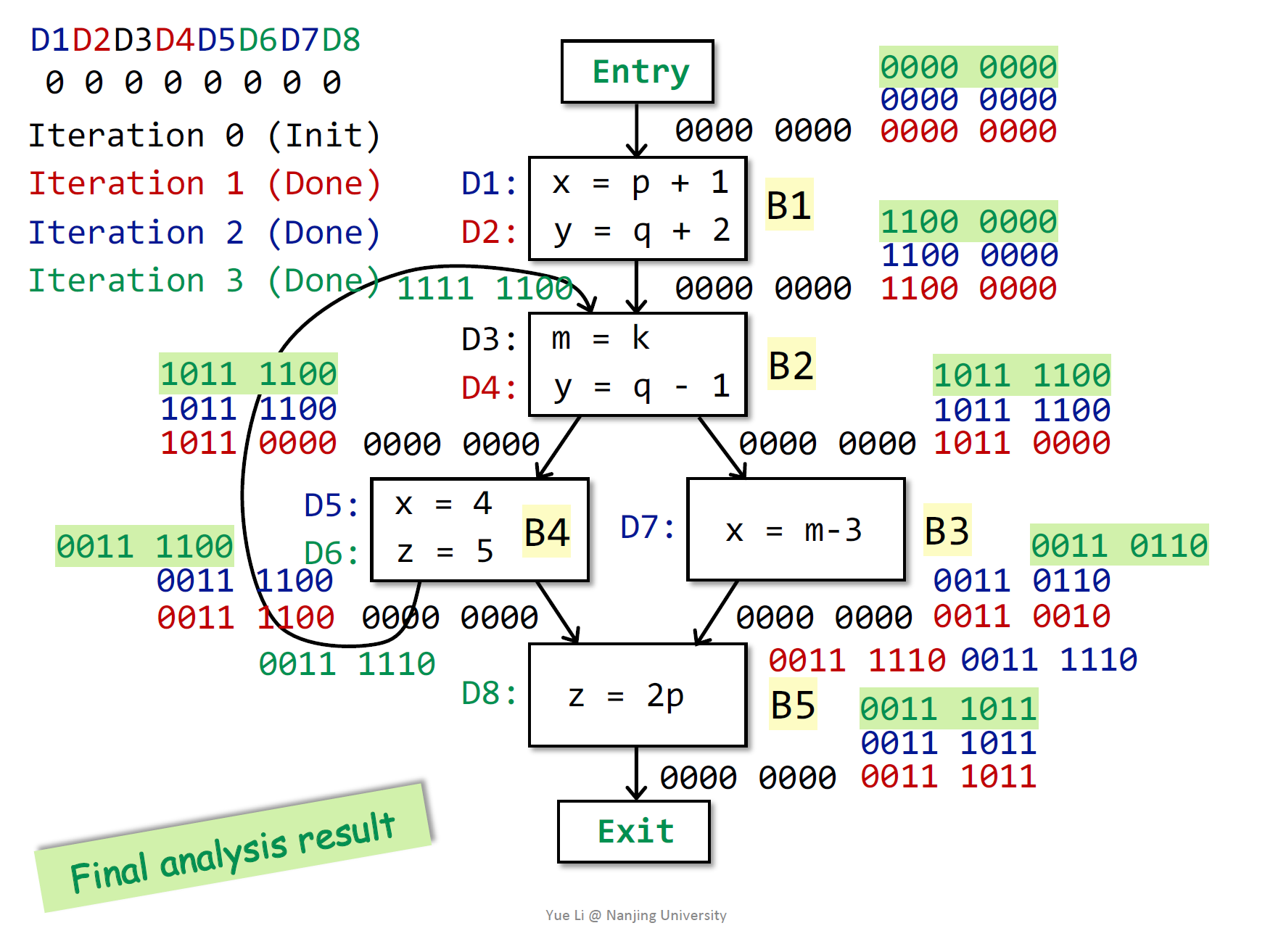
Reaching Definitions Analysis
不涉及函数调用,讨论的是方法内的CFG
变量是别名的形式(指针分析,别名分析,指向分析)

reaching definition
- 存在一条路径能到达
- 不能被二次赋值

编译优化会用到,也可以用来分析undefined variable
是一种may-Analysis,过拟合
100个定义用100个definition来定义


给出了转移函数的定义
因为无法确定BB之间的前驱关系,所有定义了当前BB内的定义的语句都需要被kill掉
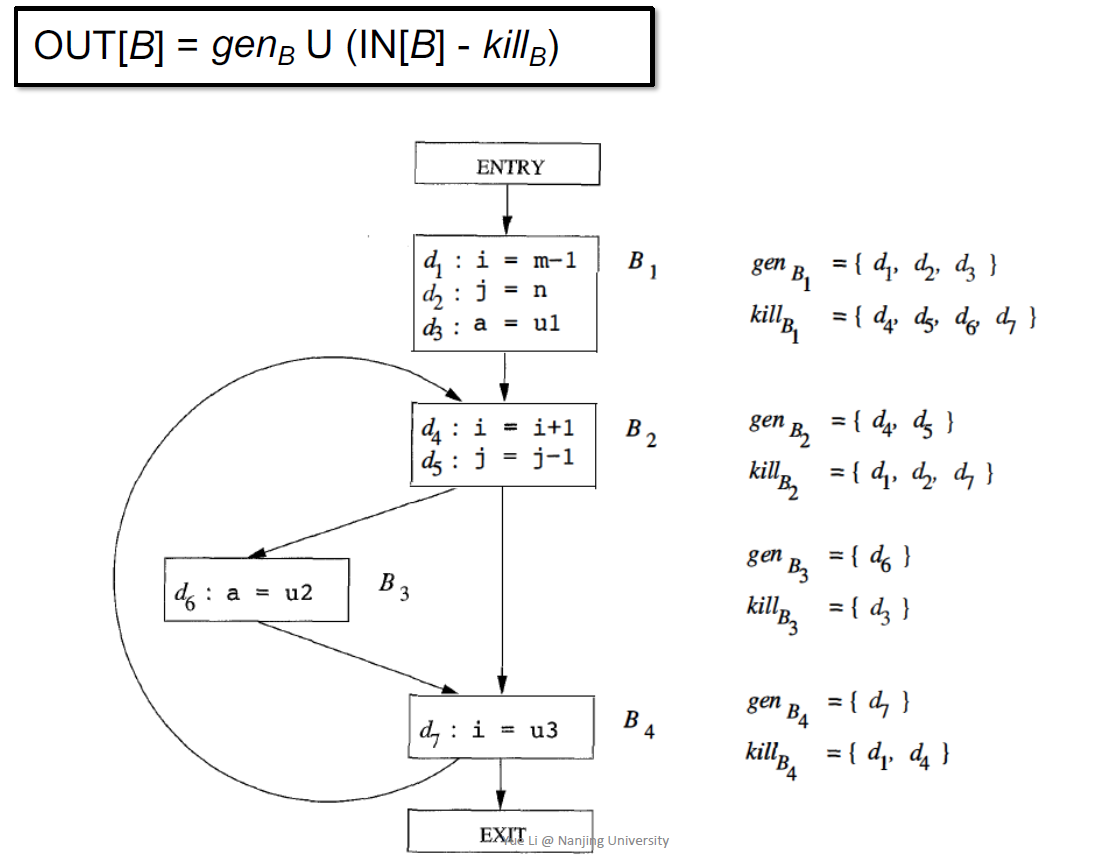
对于control flow进行分析,定义
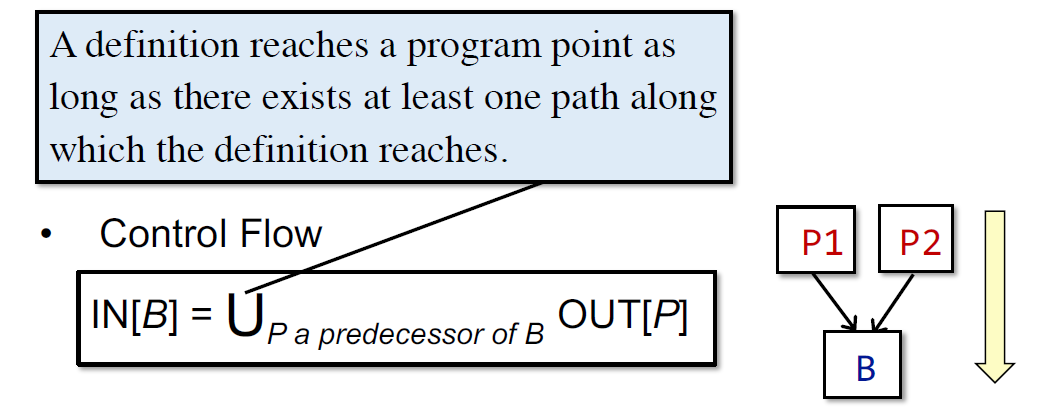
入口的output为空,entry没有定义 (may analyse一般为空,must analyse一般考虑为undefined)
除了entry的BB的output都为空(程序都没运行)
当任何OUT改变的话
会停机吗?

B3的Input=10110000
B3的Output=00000010 union (10110000 - 10001000) = 00000010 union 00110000 = 00110010
上一轮的BB的out都是空,全变了,再循环一轮
B2的out= 10111100
B3的out= 00110110
根据转移函数的定义,当输入不变时输出不变
如何证明算法的收敛
$OUT[S]=gen_s\cup (IN[S] -kill_s)$
- $gen_s \text{和}kill_s$不变
- more facts加入后,只会让多+1而不会多kill,单调递增的感觉
- facts是有限的
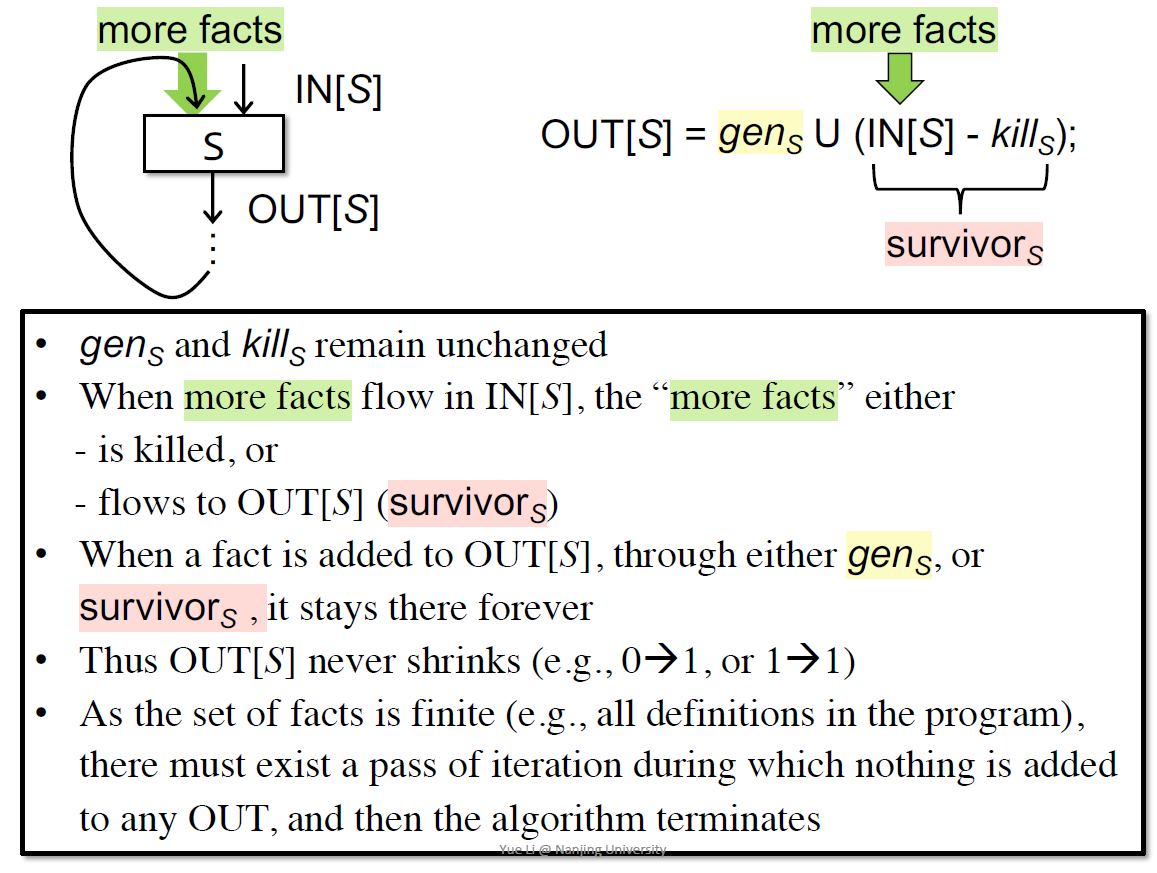
为什么每个out不再变化就说明停机了?
Out不变,In不变,Out不变
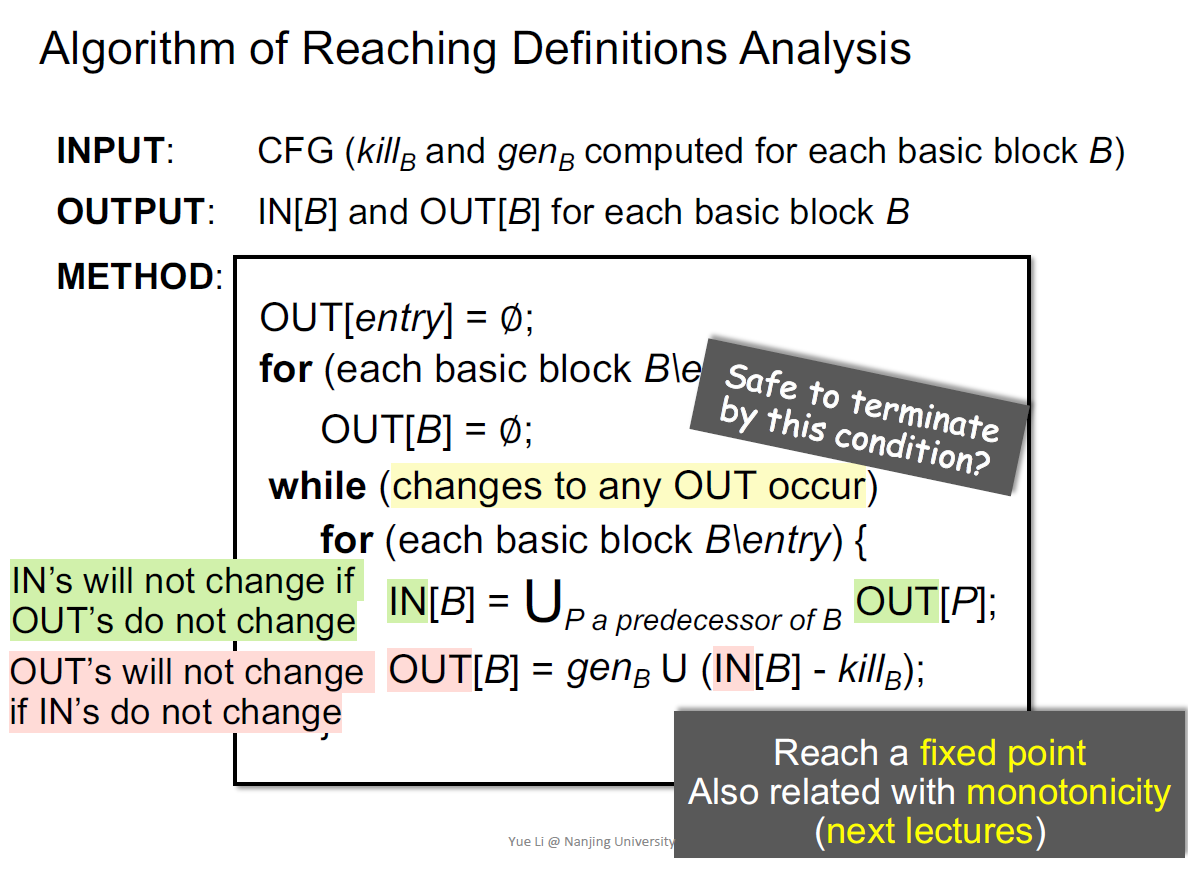
算法到达了不动点,和单调性相关
Live Variables Analysis
数据流分析的应用,归结为在格上求解不动点的问题
一般分析算法求出的是最大不动点和最小不动点
定义:某处变量的值是否能够在后面可以使用(用之前是live,不能被重定义)
live变量的信息可以用于寄存器分配,当寄存器满了的时候

定义中指出是some path,因此是一种may analysis,定义的直观含义是某点的变量是否会被后续用到
变量和定义的区别在哪里?
都用bit vector表示

采用backward的方法进行分析
In[B]= use_B union (Out[B] - redine[B])
通过具体情况枚举分析
use在define之前
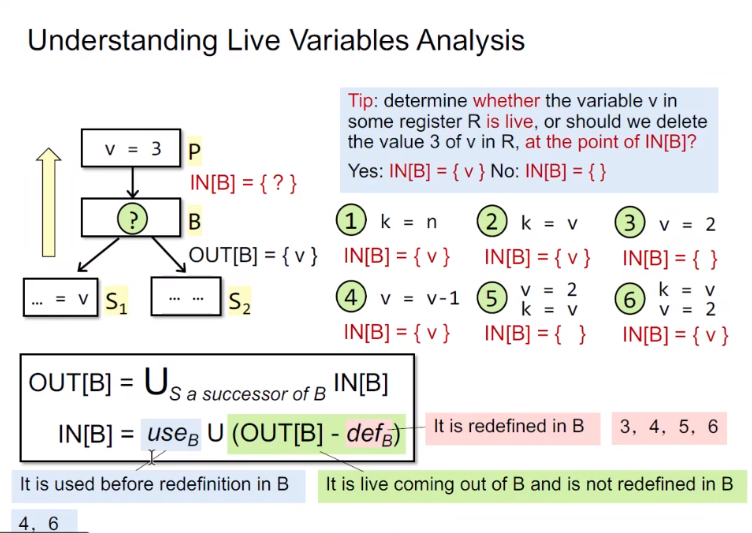
更正:此处的$OUT[B]=\cup_S IN[s]$
给定的out求in,边界条件为in=空
一般情况下may analyse的初始化是空,must analyse是all,和reaching definition定义很像

0001000
B4有两个后继,out[b4]=in[b2] union in[b5] = 0001000 union 0000000 = 0001000
in[b4]= 0100000 union (0001000 - 1000000) = 0101000
B2的Input是 100 1001,因为m是在define后用的
B1的输入0011101
第二轮
0101001
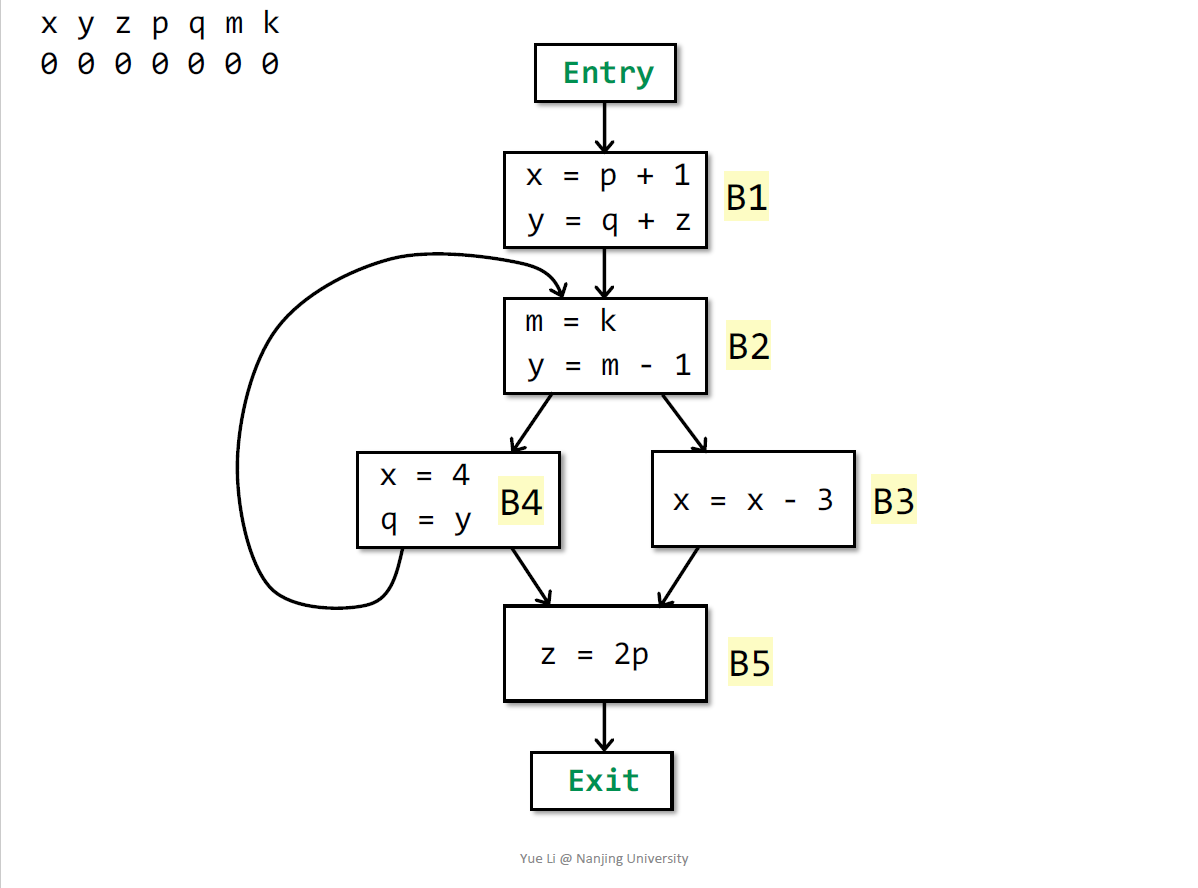
计算INPUT的顺序不同会影响迭代的次数
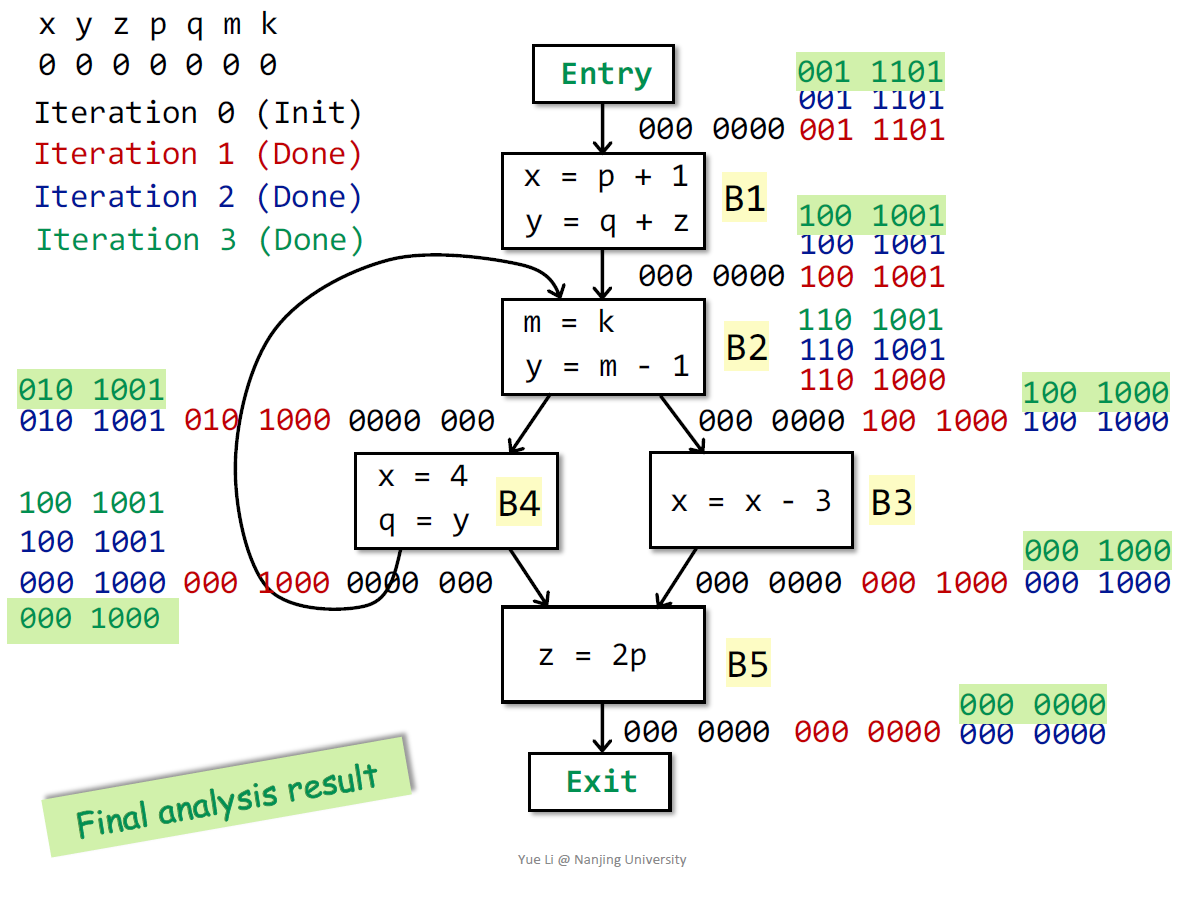
Available Expressions Analysis
一种must analysis,为了实现对程序的优化而不是解决安全问题
从程序入口到p的所有路径必须经过表达式 $x\ op\ y$,并且表达式最后的求值之后,$x$和$y$不能被重定义

类似于表达式简化的思想,p点之后对该表达式可以进行替代
首先给出抽象

是一种前向分析
out = gen union (input - kill)

两个分支后是available的
因为所有pass都必须available,输入是前驱输出的交集

优化而不是找bug,不能误报
初始化为全1(因为要交)

out[B1]=10000
out[B2]=01010 union (10000 - 10000)=01010
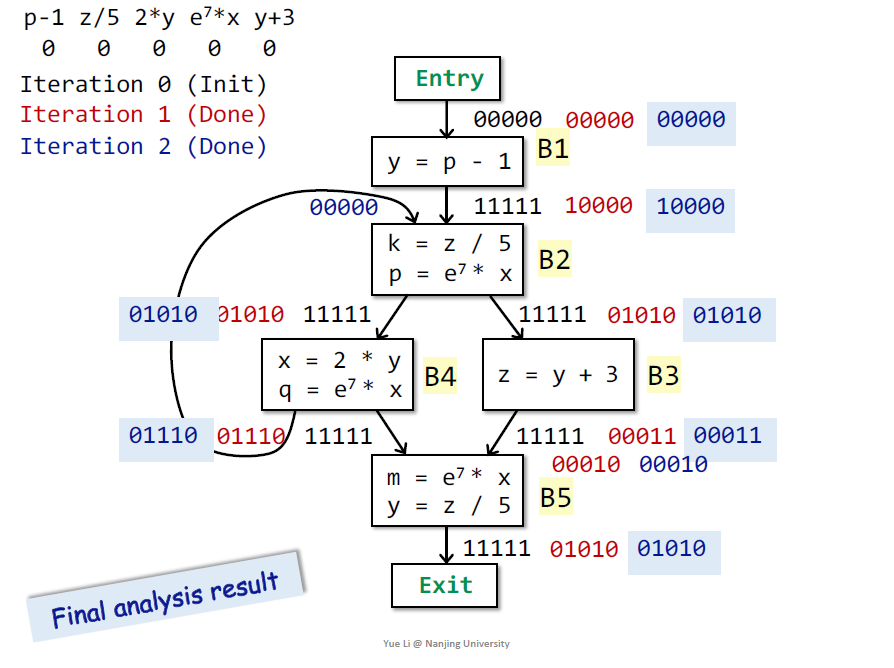
B4 input=11111, Output= 00110 union (01010-00010) =01110
先算kill再算gen,根据定义
01010 union (00010 - 00111)=01010
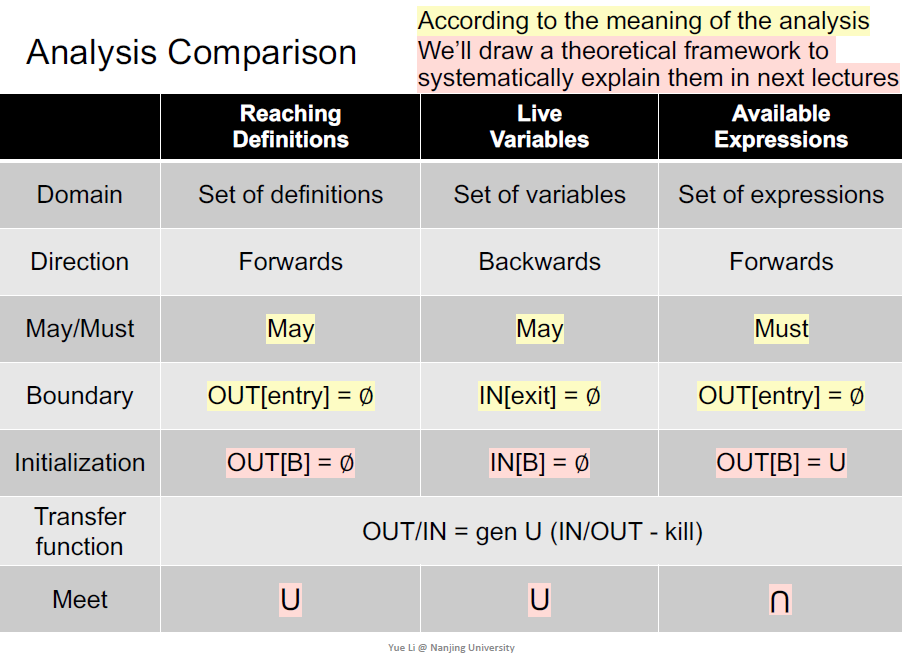
三类定义的对比

Data Flow Analysis Foundation


上节课3个应用的算法均是迭代式算法,回答存在的问题
从23的基础上定义格
复习核心内容是8
Iterative Algorithm, Another View
给定CFG,有k个statement,迭代算法每次更新节点的OUT[n]

进行形式化

实际上是不动点

- 迭代式算法一定能终止并给出一个解吗?
- 假设能达到不动点,只有一个不动点吗?如果有若干个不动点,迭代式算法得到的不动点足够精确吗?
- 迭代式算法到达不动点或得到解需要多长时间?(复杂度)

Partial Order
偏序集的定义$P,\subseteq$,带有偏序关系的集合,并满足以下关系
- 自反性
- 反对称性
- 传递性

整数集上的小于关系不是偏序关系
子串是偏序关系

偏序集的含义是不是所有的元素互相之间必须满足偏序关系,如pin和sin没有偏序关系,但是{pin,sin,sing,gin}和singing构成偏序集
幂集

Upper and Lower Bounds
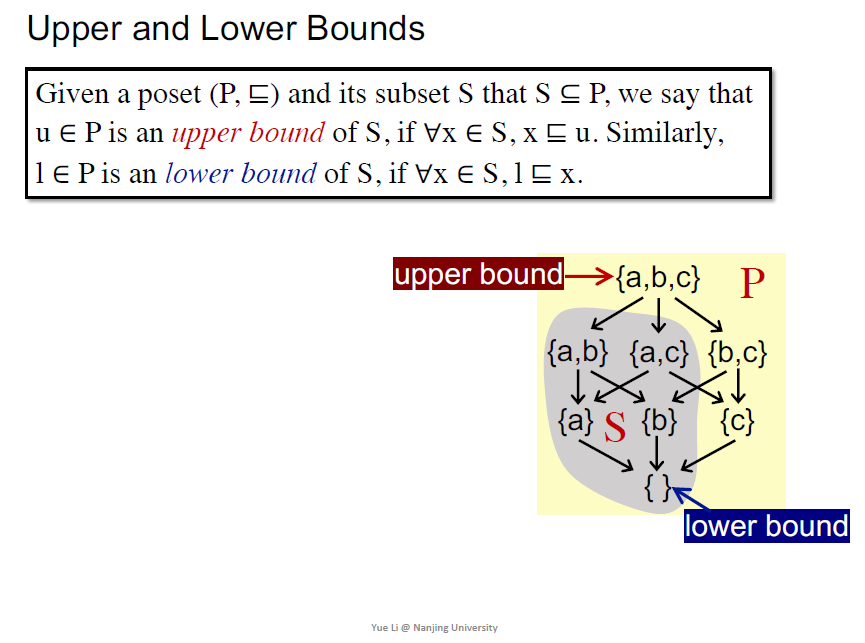
最小上界lub和最大下界glb
bound可以不在S当中,在P中即可

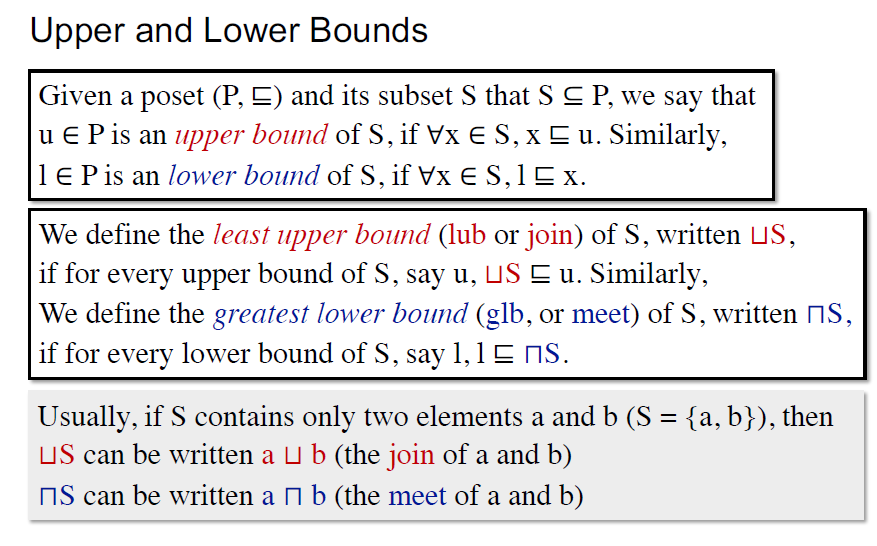
偏序集的glb和lub是唯一的
证明:反证法,反对称性

Lattice, Semilattice, Complete and Product Lattice
在程序分析中学格(
每两个元素存在glb和lub的偏序集称为格
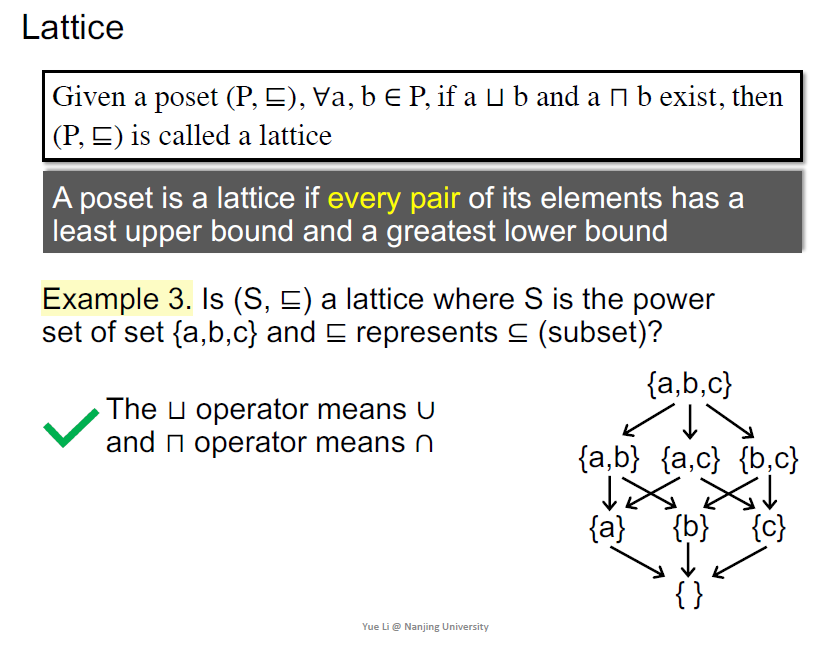
半格:任意两个元素只存在glb或者lub
- 只存在glb,称为meet半格
- 只存在lub,称为join半格

全格
格的任意一个子集,均存在glb和lub

整数集的子集为什么不是全格,但是格?

回顾格的定义,任意两个元素存在glb和lub即可;全格要求所有子集都有glb和lub
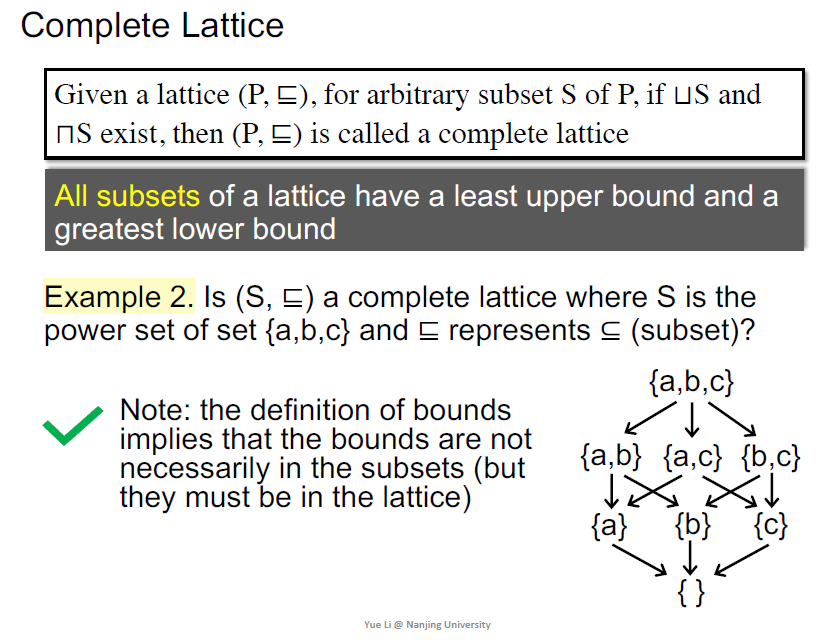
有限的格一定是全格,complete的lattice一定是有限的吗,不是
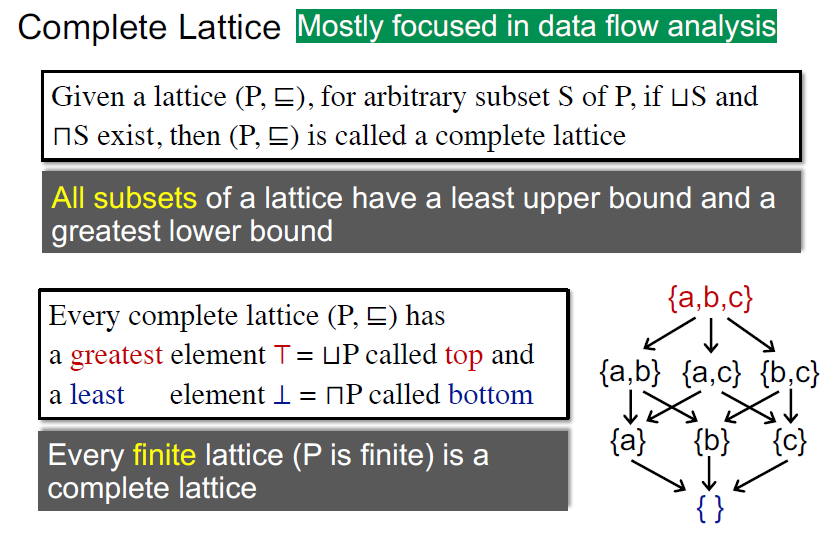
一般程序内的是有限的
积格的定义

- 积格的lub:实际上是每个格内两个元素的lub
- 积格的glb:每个格内的两个元素的glb
性质
- 根据定义,积格也是格
- 积格是全格的积时,积格也是全格
Data Flow Analysis Framework via Lattice
介绍格是为了用格形式化数据流分析
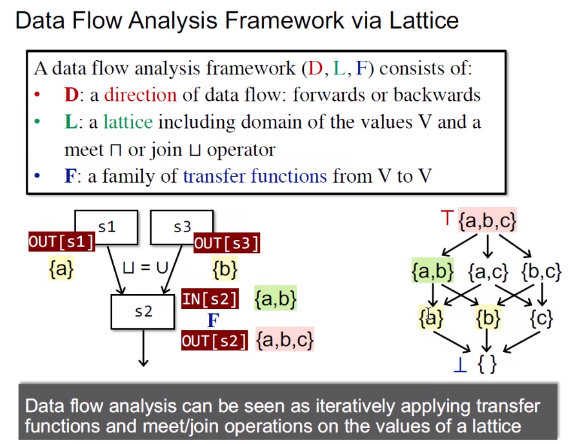
有点类似沿着控制流上升到上界
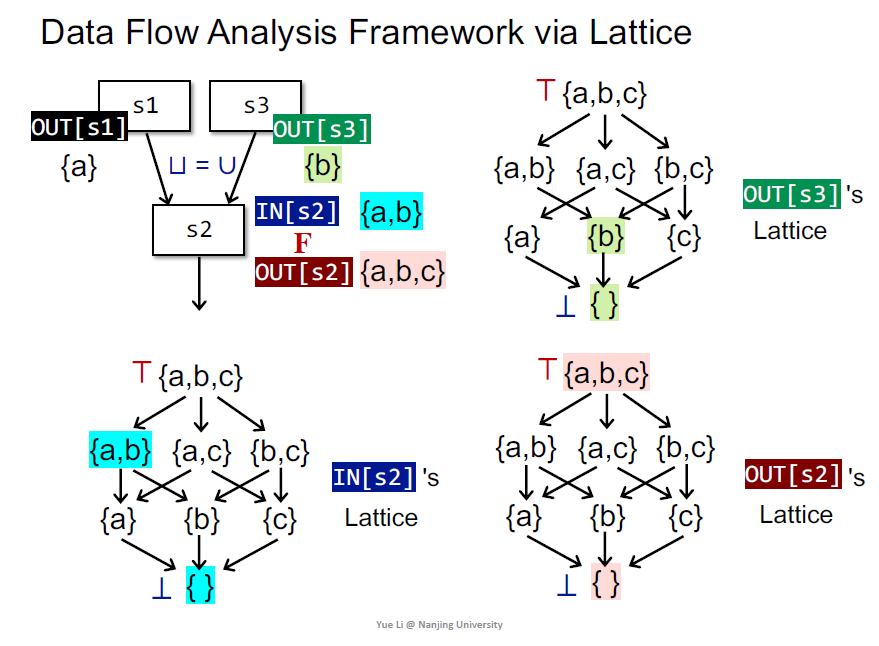
试图回答第1个问题

需要单调性和不动点定理
Monoticity and Fixed point Theorem
前面提到complete的格不一定是有限的,所以这里额外第二个条件是finite
从bottom出发,迭代f函数能够找到的第一个不动点叫做最小不动点;从top出发,求到的是最大不动点

证明不动点的存在:
根据$\perp$的定义,有$\perp \subseteq f(\perp)$
根据单调性的定义,$f(\perp)\subseteq f(f(\perp))$
递归地有 $\perp \subseteq f(\perp) \subseteq \dots f^i(\perp)$
根据$L$的有限性,存在一个$k$,$f^k(\perp)=f^{k+1}(\perp)=f^{fix}$
即存在不动点,回答了问题1
(可以假设不存在不动点,则根据单调性和有限性推出矛盾)

再证明得到的不动点是最小不动点
设存在另一个不动点为$x=f(x)$
根据$\perp$的定义,有$\perp \subseteq x$
根据单调性有 $f(\perp) \subseteq f(x)$ (数学归纳法的奠基)
采用数学归纳法,假设$f^i(\perp)\subseteq f^i(x)$
根据单调性,有$f^{i+1}(\perp)\subseteq f^{i+1}(x)=f(x)$
则有$f^{fix}=f^k(\perp)\subseteq f^k(x)=x$
即证明了求出的不动点是最小不动点,回答了问题2
间接证明了求出的不动点的唯一性

依然存在的问题,仅回答了lattice上函数的性质,没有和迭代式算法建立联系

Relate Iterative Algorithm to Fixed Point Theorem

关键是F的单调性

先证明两个运算的单调性
思路是利用最小上界的定义 偏序关系的传递性
证明下确界运算的思路类似

最后解答复杂性的问题
先介绍格的高度的定义
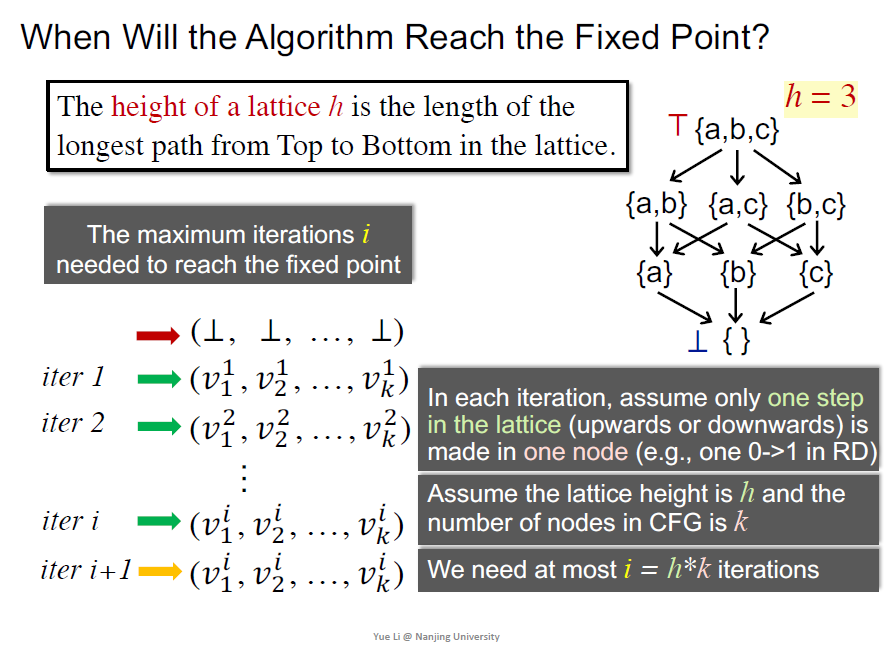

复杂度取决于CFG节点个数和格的高度
May/Must Analysis, A Lattive View
先抽象成一个积格进行理解,先看may alalysis
以reaching definition为例,作为一种may analysis 最下面No definitions can reach是所有变量都被初始化了,最上面是所有变量都可能被redefine,safe是指从找bug的角度,给所有变量报错是safe but useless,因此需要从下往上找到safe和unsafe的边界 truth
如何判断是否超过了truth(根据不动点
设计transfer function和cf merge的原则是safe approximation
根据单调性,求得的是最小不动点
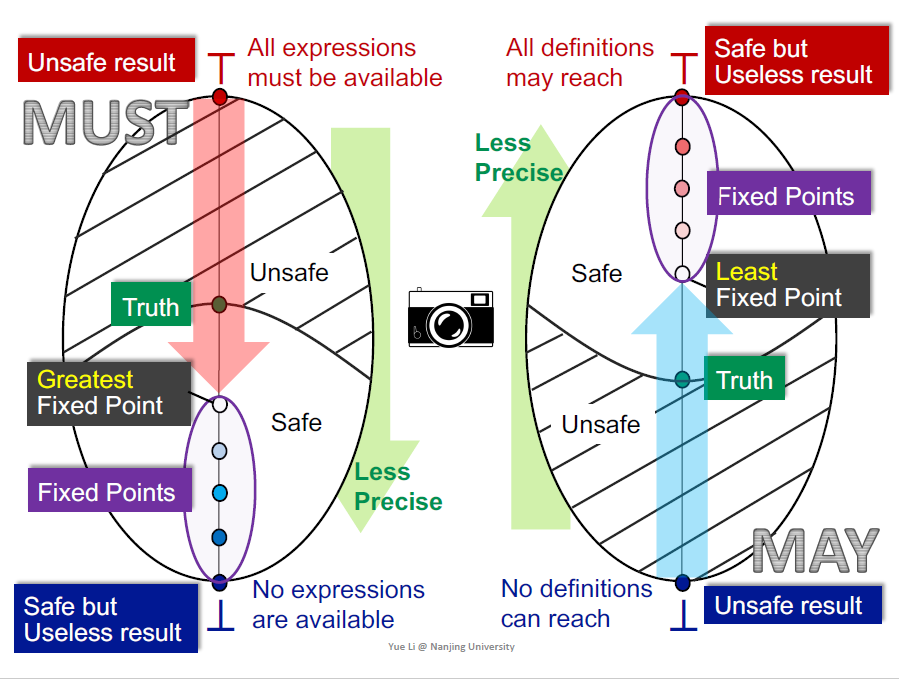
must analyse解决的是优化问题,从top出发,所有表达式都能优化显然是错误的,bottom是安全的但是没用的,没有表达式可以优化
must analyse的分析不能有误报,要求是complete
另一个维度理解may的最小不动点:transfer function是固定的,join是求最小上界,每次迭代走的是minimal step,因此得到的是最小不动点
Distributivity and MOP
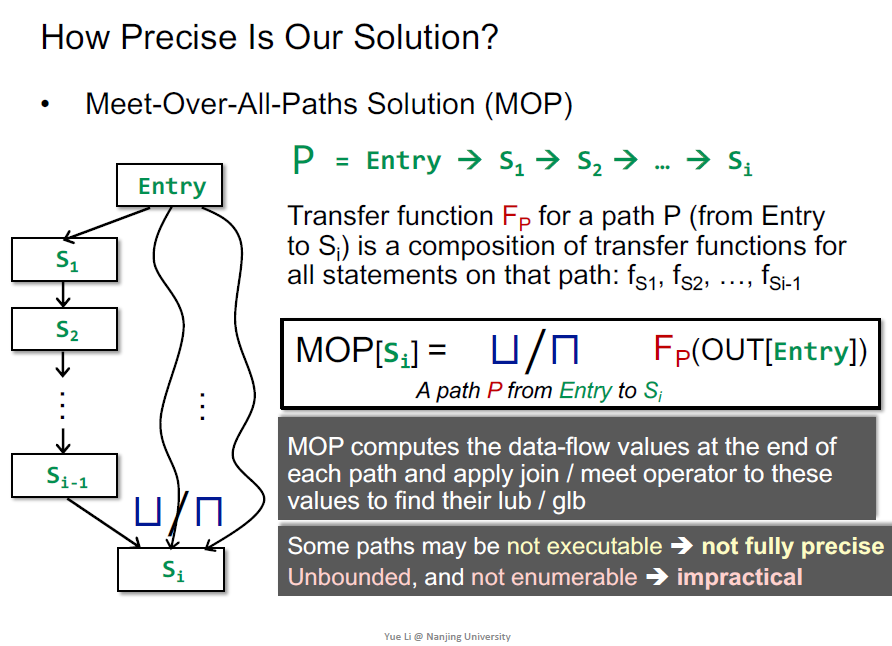
考虑解的精确性,MOP是衡量的一个指标
总的transfer function就是各个f的组合
MOP是枚举所有的path的结果再join或meet(计算了每条路径最终的值
静态分析中有的路径可能是不可达的,导致结果不是完全精确的
实际上是不可枚举的
和迭代式算法的区别
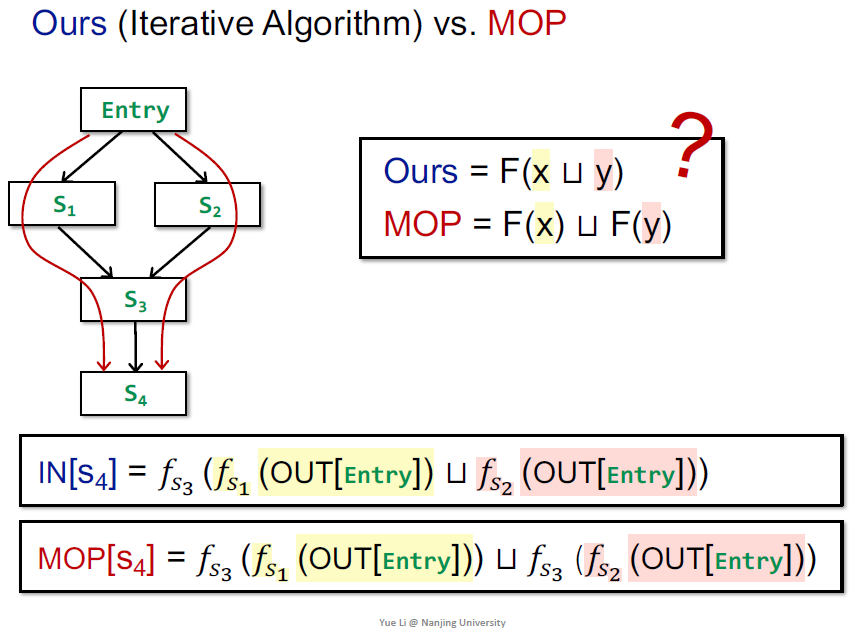
x和y之间的关系
最小上界小于上界
所以MOP更准确

当F满足分配律,两者一样准确
之前提到的bit-vector或Gen/Kill问题都是distributive

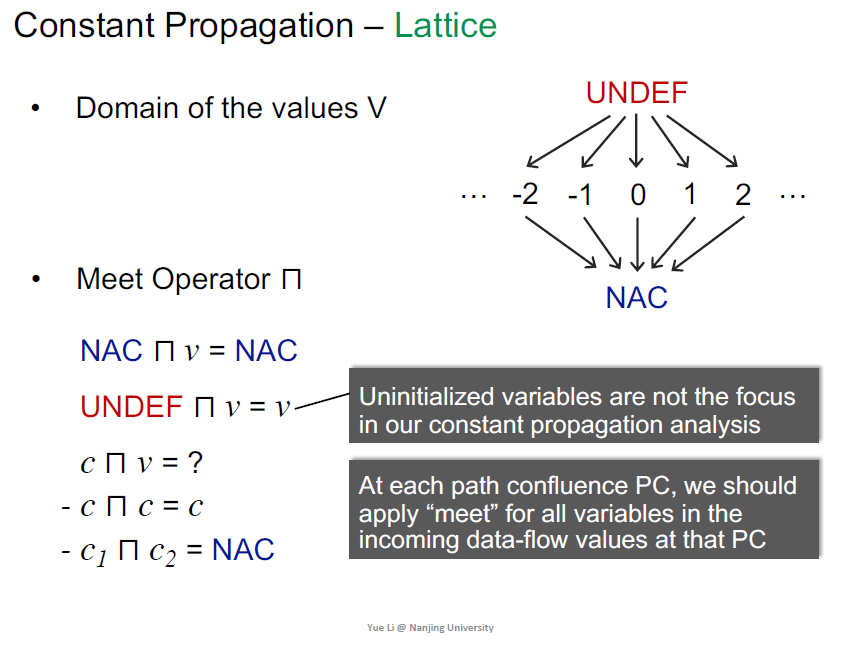
Constant Propagation
这个DFA不是distributive的

NAC: not a constant
一般不考虑未初始化的问题
对于两个常量分类讨论
关注赋值语句,kill掉与被赋值相关的常量

例子

Worklist Algorithm
区别于迭代算法,实际的工具不采用迭代算法,worklist可以看做优化
回顾迭代式算法
仅遍历计算in变了的部分


Interprocedural Analysis
过程间分析
Motivation

过程内分析对方法调用进行最保守的假设,可以做任何事情
问题:过于保守,降低了精度
过程间分析需要call graph,调用的目的地址

Call graph
call edge连接call site和callee
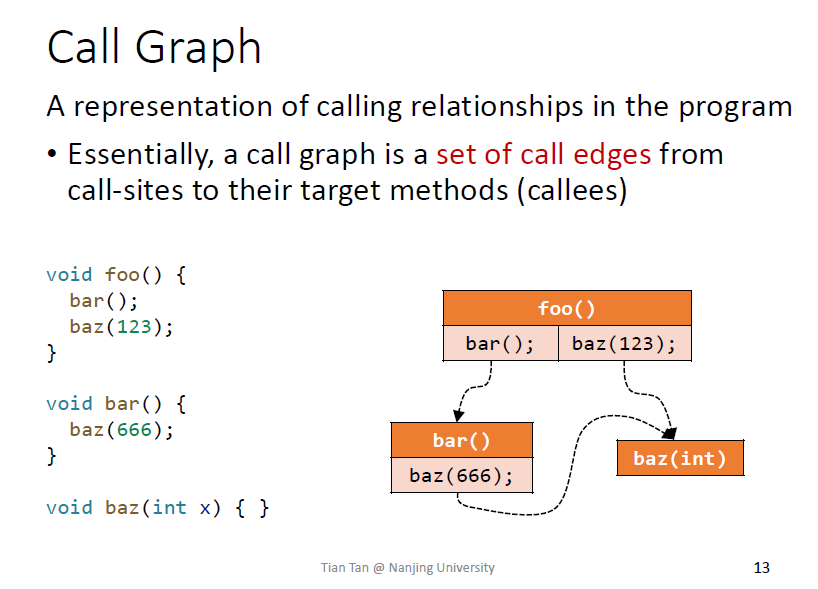

主要针对面向对象的语言,给出了4个算法

virtualcall实现多态,难以处理
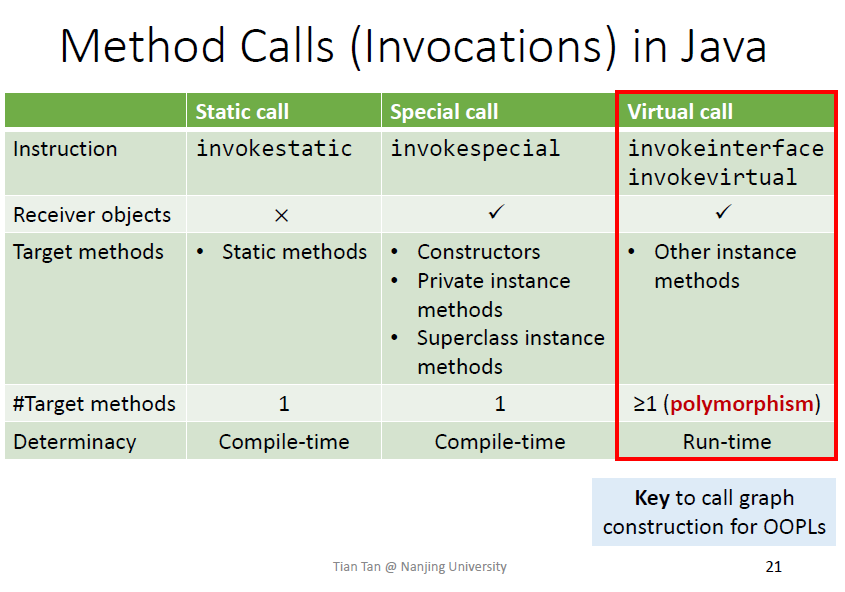
具体调用的方法在运行时确定,取决于
- 对象的类型
- 方法签名(可以唯一确定一个方法

优先当前类有方法体的方法,不能是抽象的,如果没有则去父类找

CHA需要类的继承的信息,根据A的类型来决定对应的call
OO语言的顶会

算法采用分类讨论

static call最简单
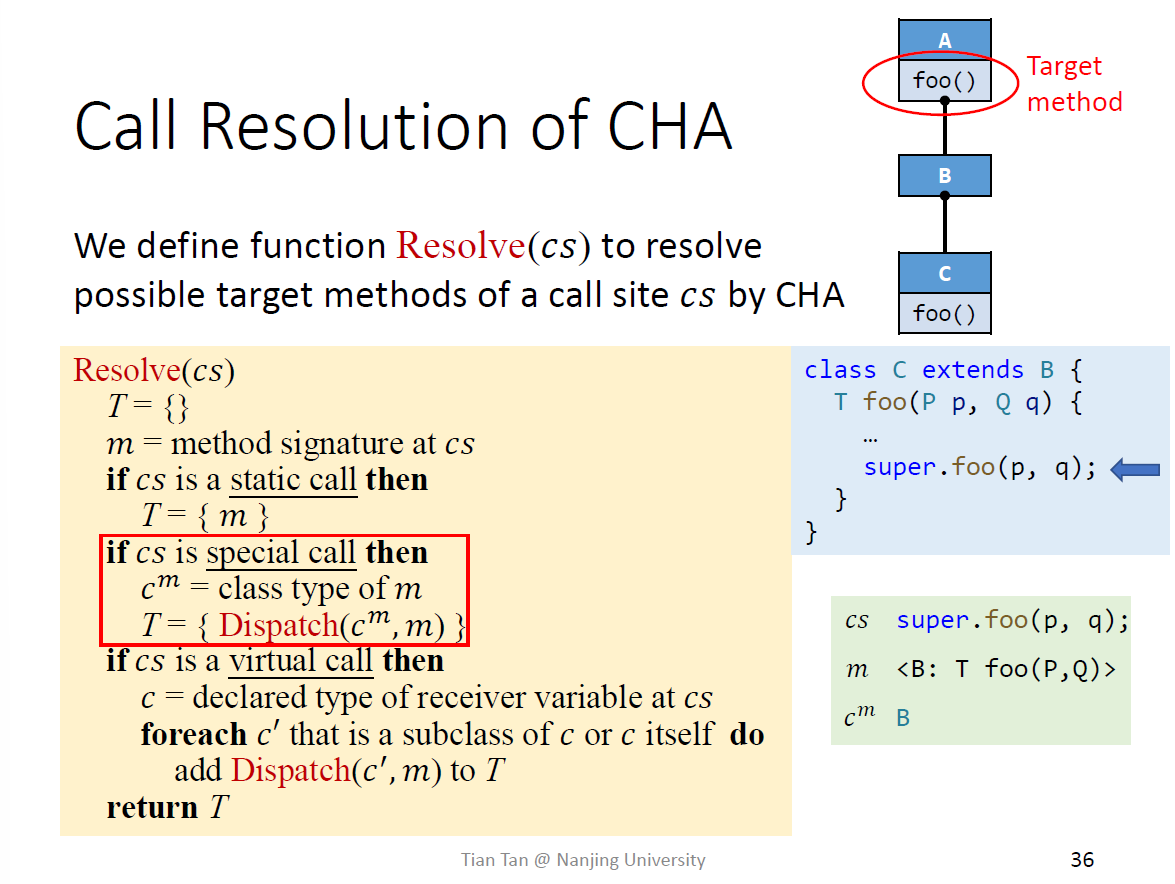
B类可能没有foo,因此需要一个Dispatch而不是直接用B.foo()\
私有和构造函数都能用dispatch解决

对于virtual call,包含了所有的子类的方法,因为

例子都属于virtual call
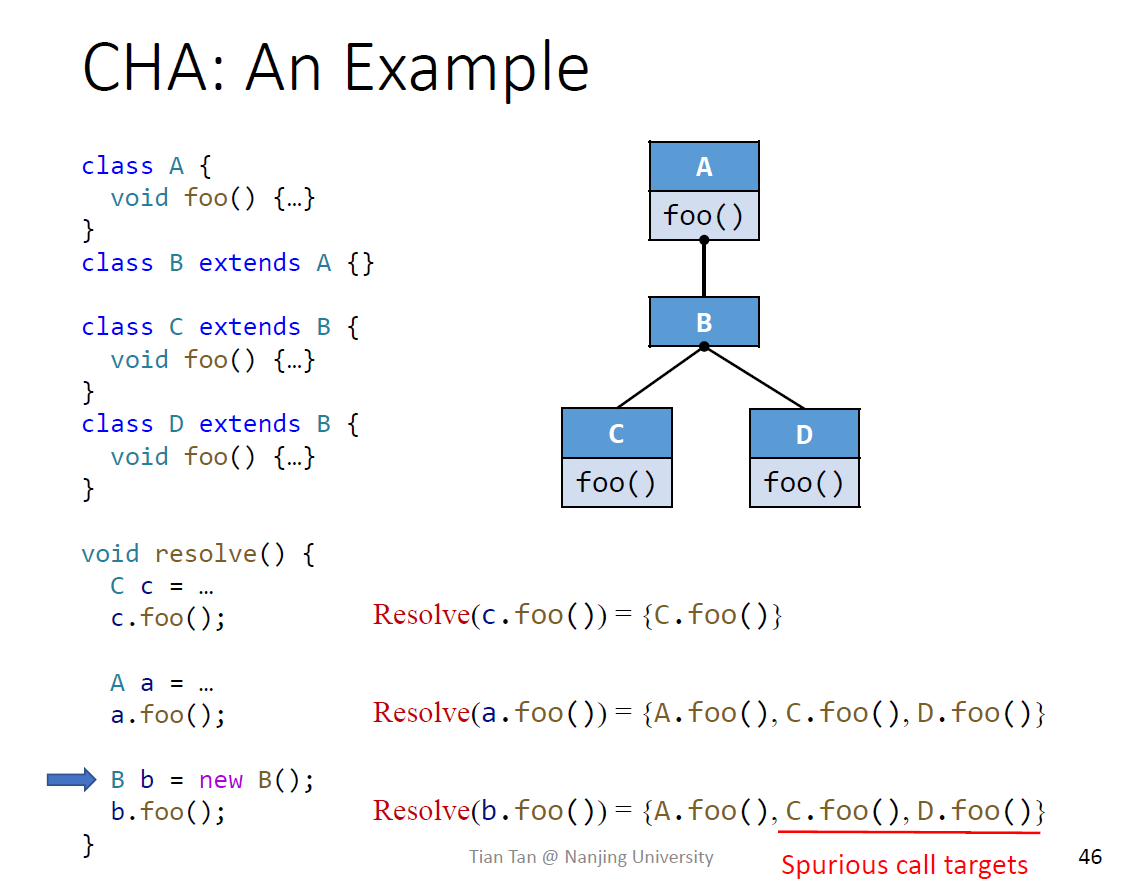
{C.foo()}
{A.foo(), C.foo(), D.foo()}
{A.foo(), C.foo(), D.foo()}
如果B b =new B(), Resolve(b.foo())={A.foo(), C.foo(), D.foo()} 结果不变
这里是一个special call吗?不是因为Java支持动态方法分配,且涉及到了继承关系
因为算法只考虑变量的声明类型
一般用在IDE中

navigate菜单中

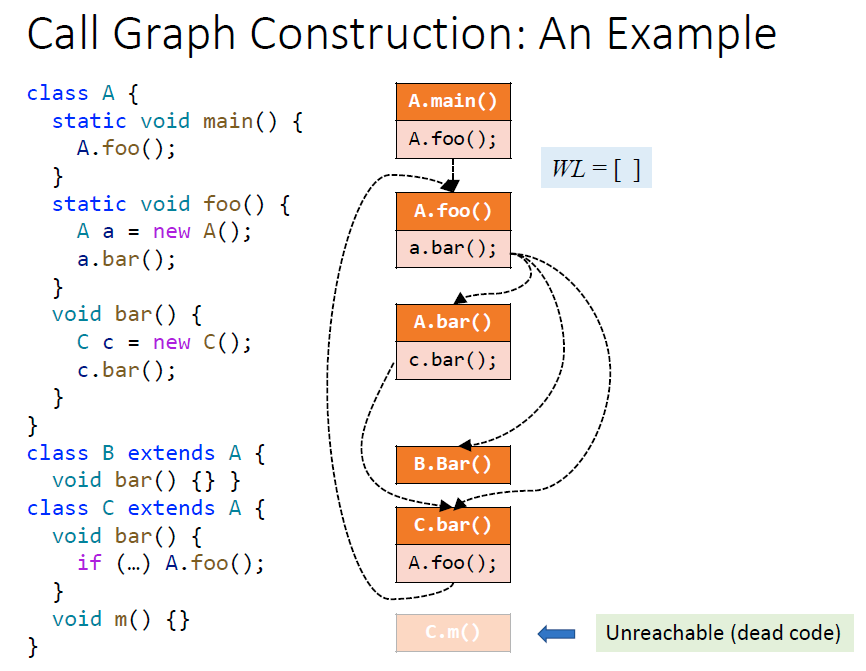
reachable是处理过的方法
通过resolve发现新的方法

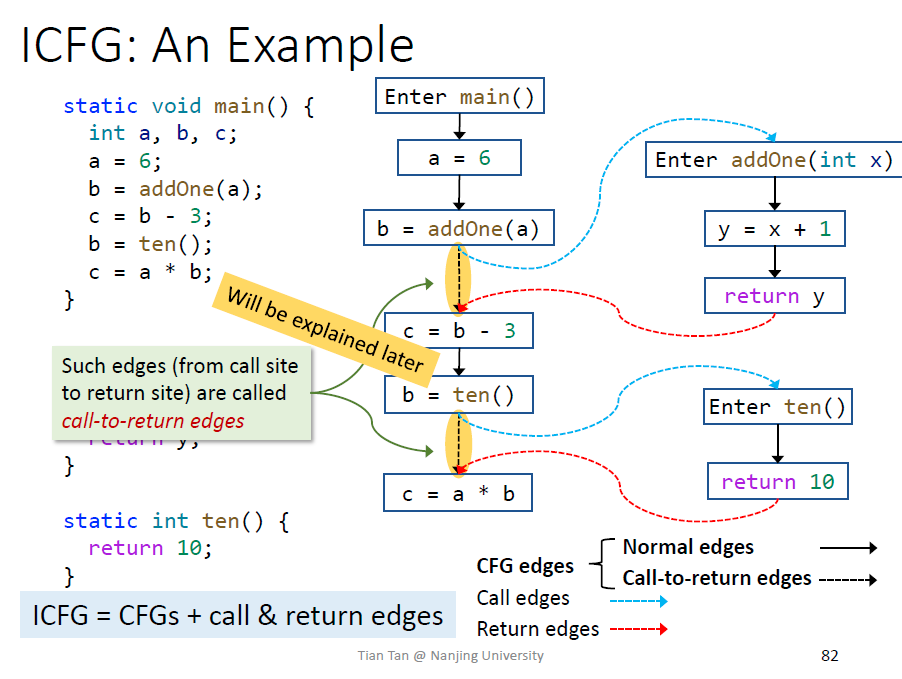
Interprocedural CFG
ICFG表示的是整个程序的结构
紧跟着call site的就是return site,利用call graph来解决ICFG

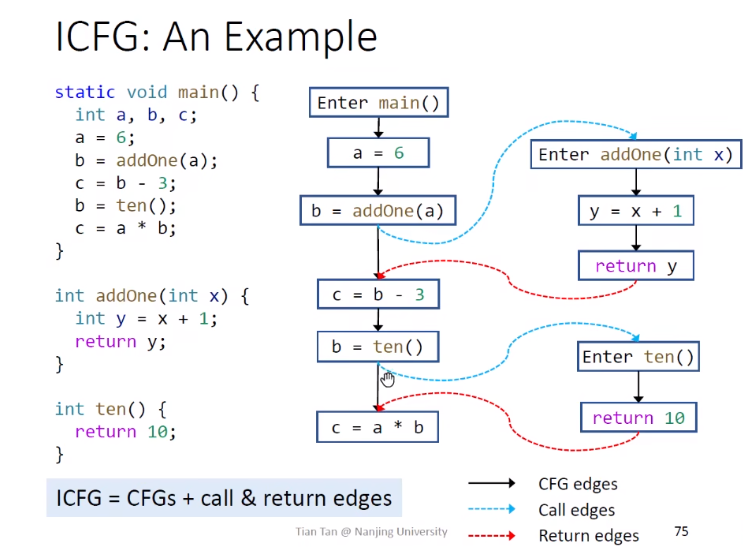
为什么还保留一条额外的边
Interprocedural Data Flow Analysis

遇到call node需要kill掉left hand side variable的值
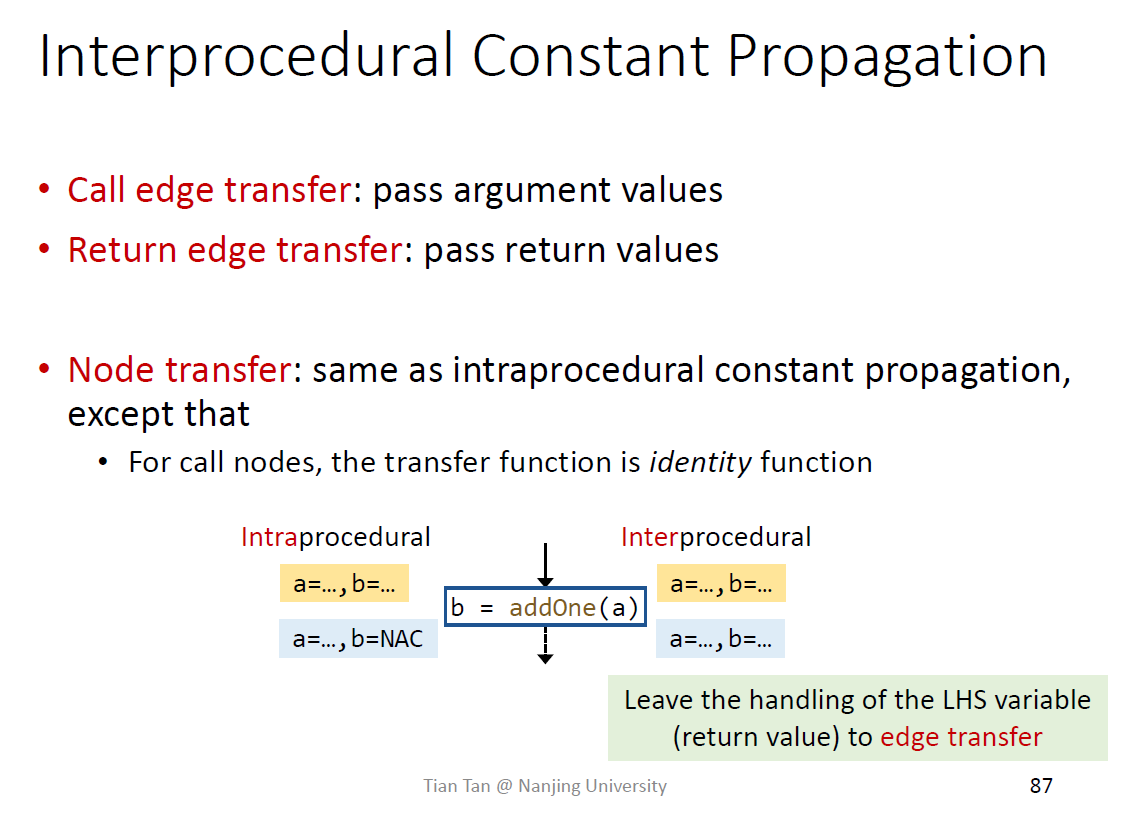
edge transfer就是给形参赋值
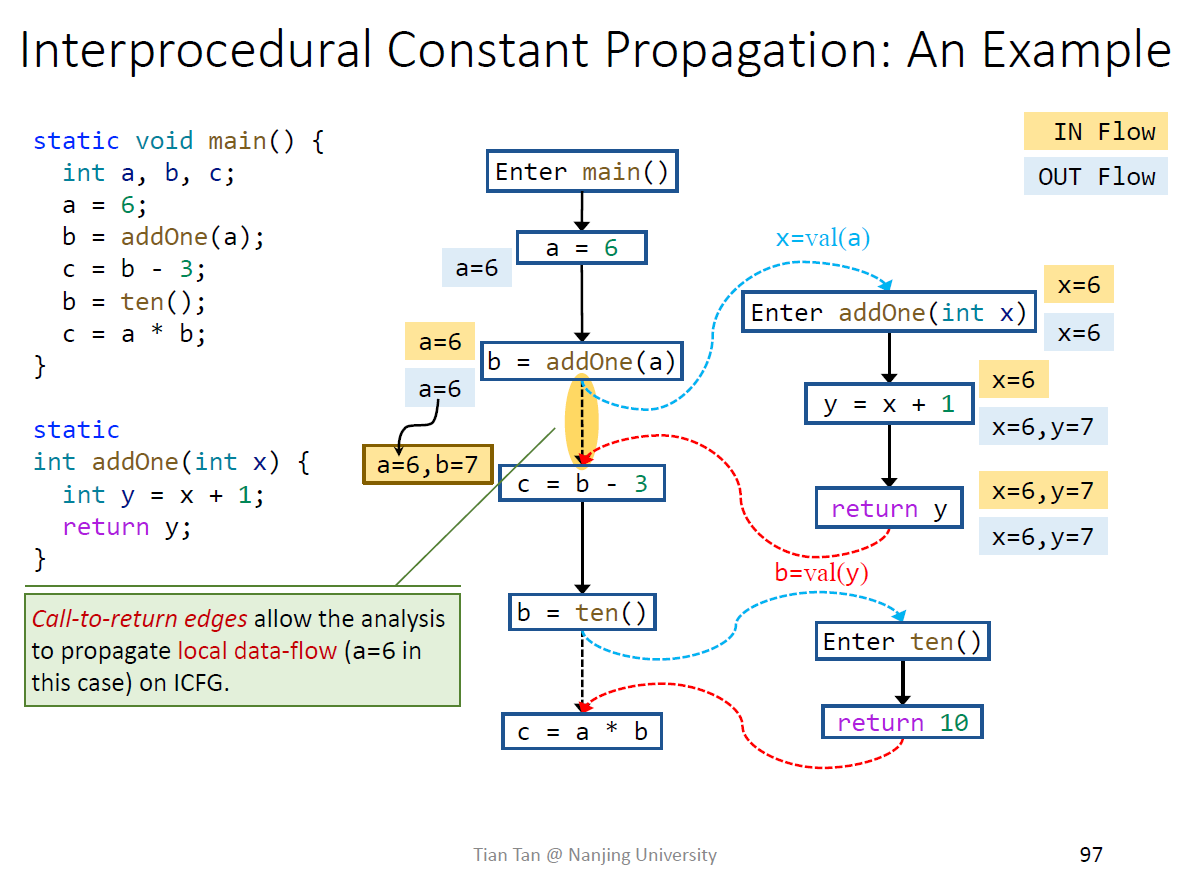
保留call to return edge是为了保证本地数据流关系的保留,即函数内部的
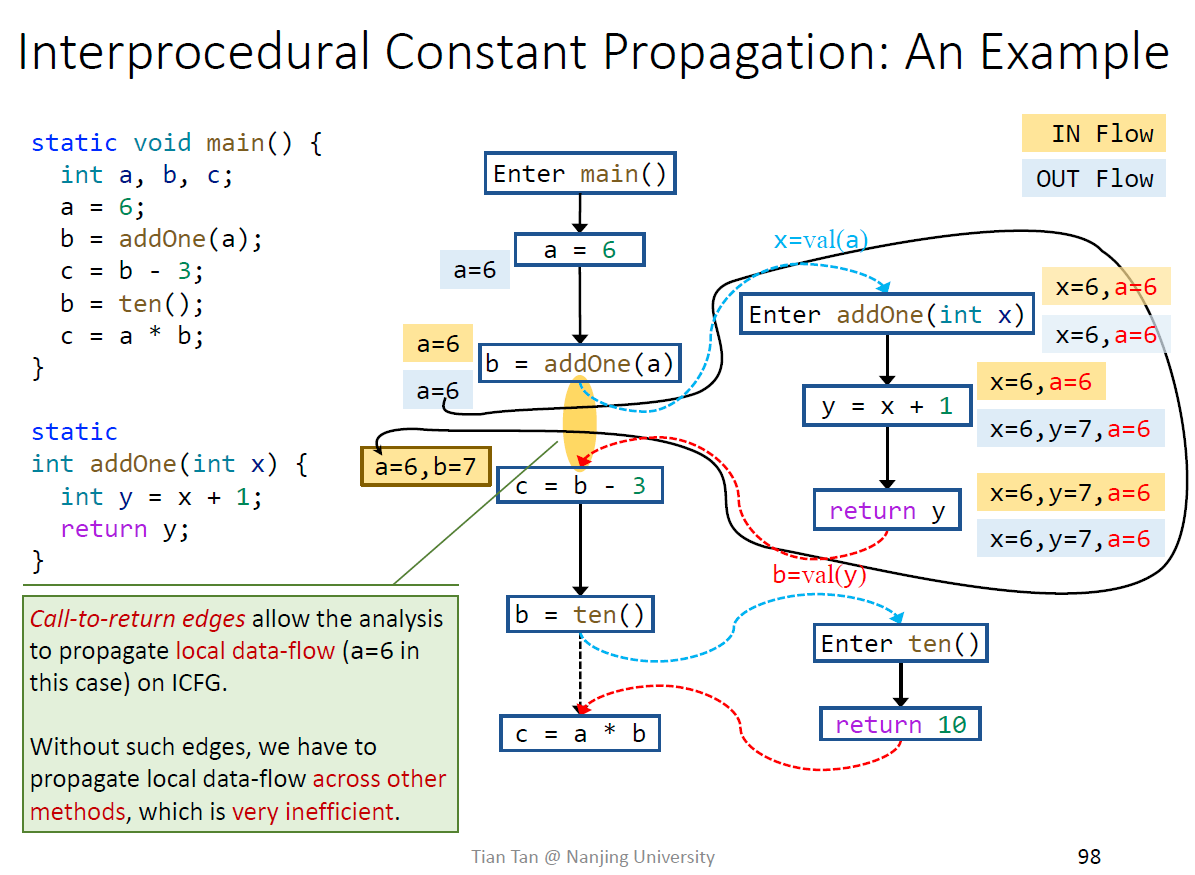
如果没有这条边,相当于函数addOne内还需要维护a的值,如下图,效率很低
kill的具体原因,需要用返回值覆盖
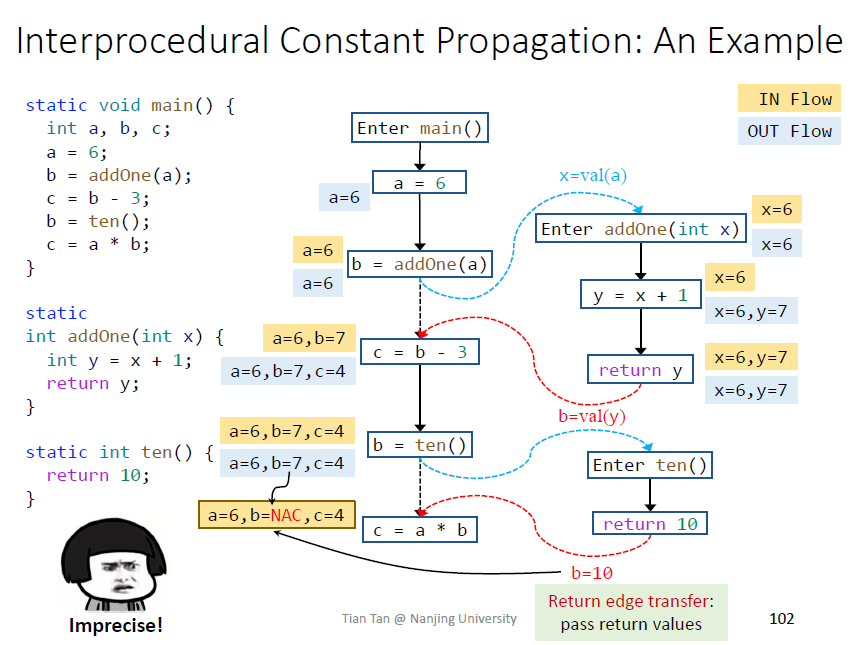
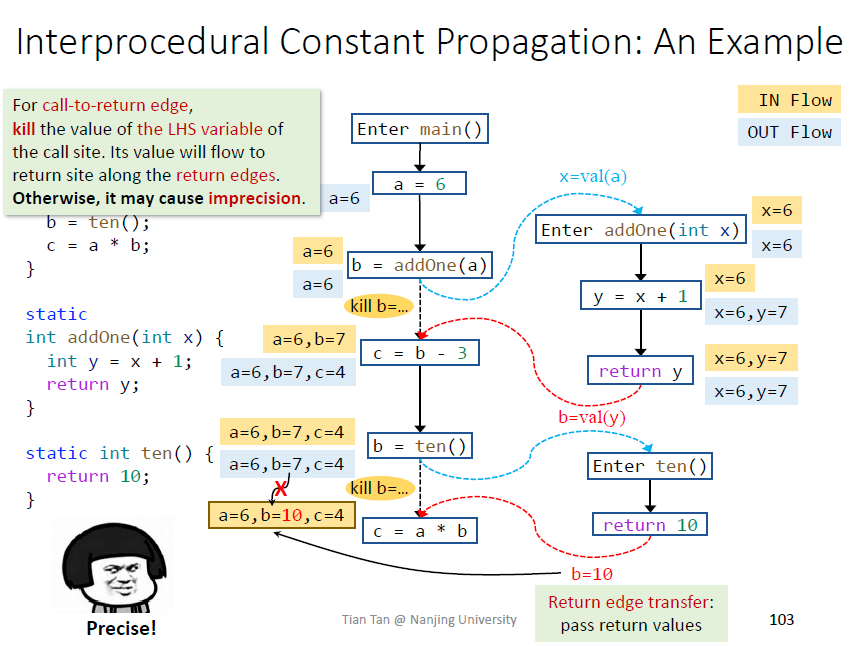
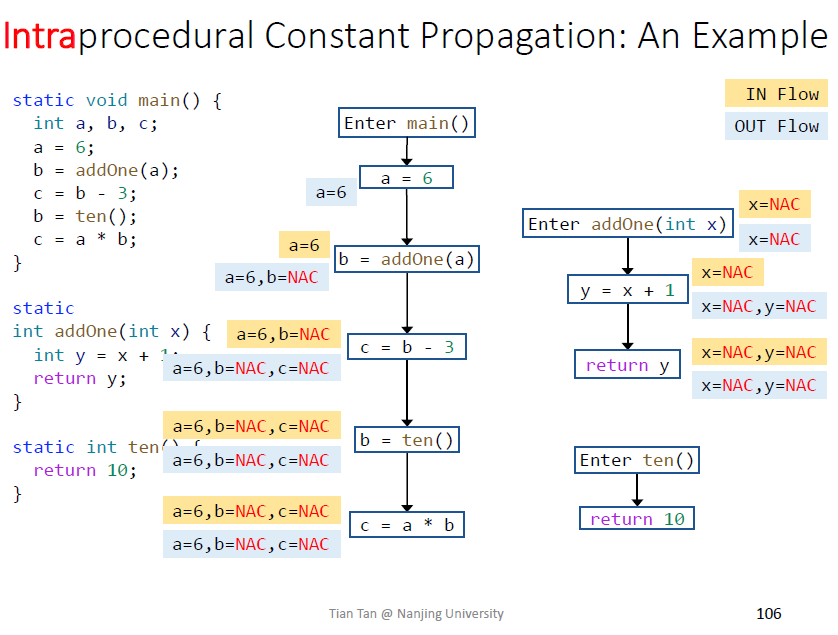
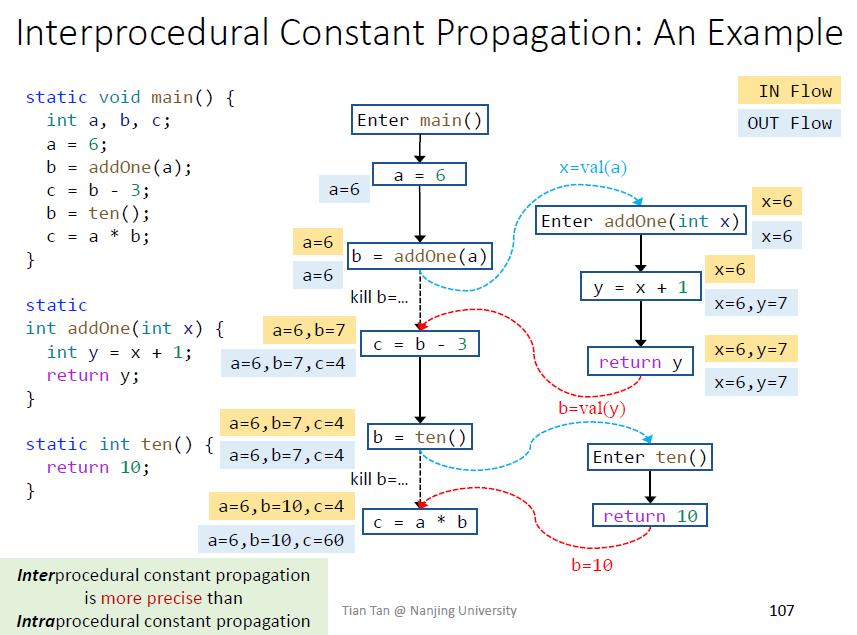
如果是过程内分析,会进行最保守的假设,所有调用返回值都是NAC,imprecise
过程间分析更加精确

Pointer Analysis Introduction
Motivation
利用CHA来求目标方法会有多个,不精确
CHA利用对象的类和子类来分析
如果对x进行常量传播,x是NAC
指针分析更精确

Introduction to Pointer Analysis
指针分析回答指针可以指向哪些地址
作为一种may analysis,过近似,给出可能指向的所有地址

OO语言内的指针包括filed和variable
指针分析的输入是一段程序,输出是如右表所示的表格

Alias Analysis别名分析
指针分析:指针可以指向哪些对象
别名分析:两个指针能否指向同一地址
显然,可以利用指针分析实现别名分析

指针分析的应用:
- 计算调用图
- 编译优化
- 漏洞检测 空指针
- …

Key Factors
非常复杂,在精度和效率之间取舍

Heap Abstraction
堆抽象:如何对堆内存建模
因为在动态执行中,堆的对象可能是无穷的,静态分析需要在一定时间内得出结果,堆抽象需要将具体的对象抽象成有限数量的抽象的对象

了解有两大流派,学习allocation sites技术
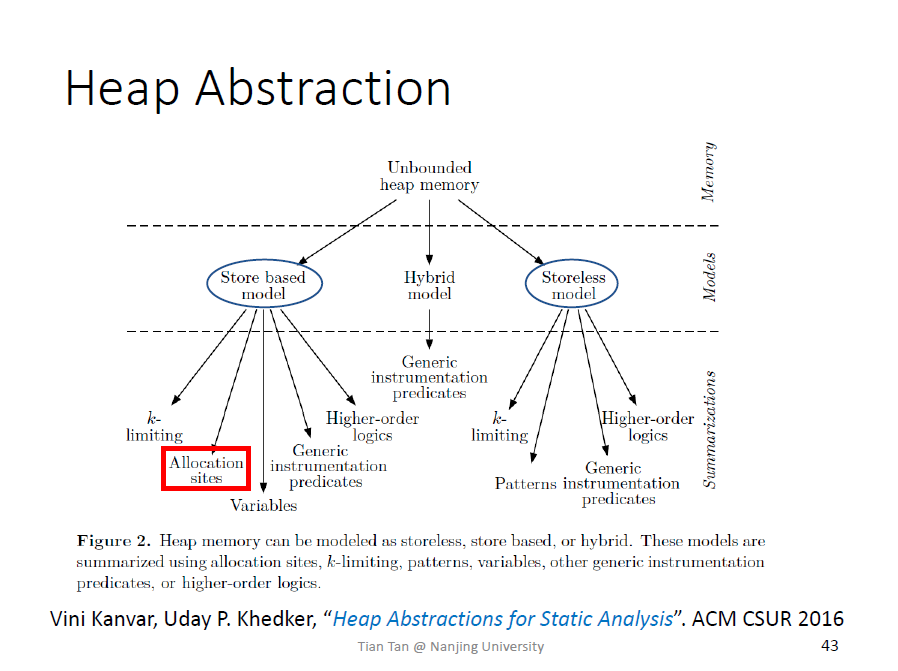
根据对象的创建点来建模,$O_2$表示创建点
因为程序中创建对象的语句是有限的,显然抽象的对象数量是有限的
Context Sensitivity
上下文:考虑如何对调用点建模
方法可能被调用很多次,对应不同的上下文时,方法内的调用可能不同
上下文敏感可以模拟 区分不同的上下文,上下文不同时,对同一个方法分析多次
上下文不敏感每个方法仅分析一次
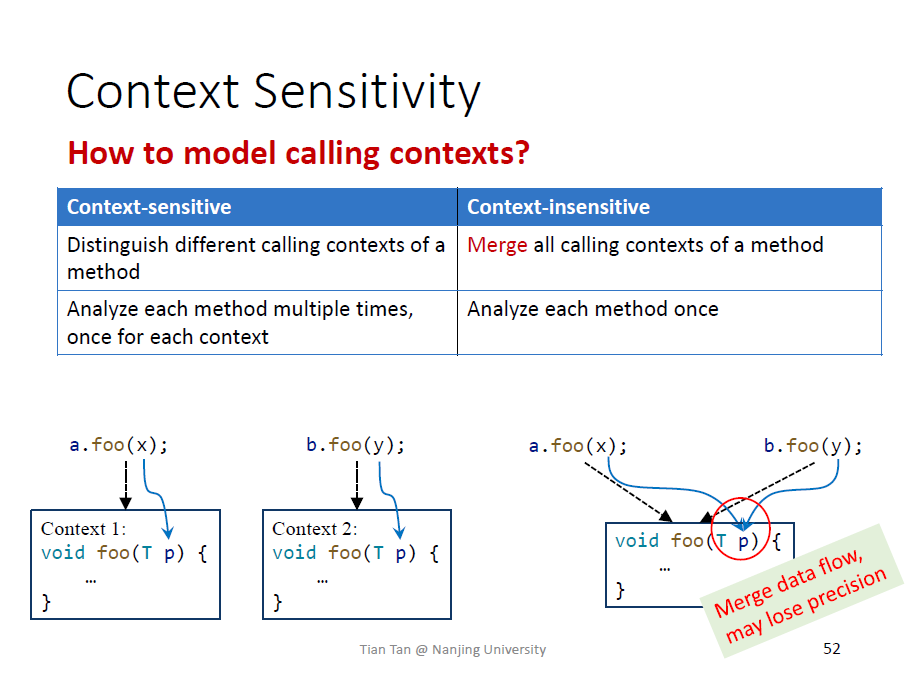
上下文敏感可以显著提高精度
学习计划是先学习不敏感,再学习敏感
Flow Sensitivity
指如何对控制流进行建模
- 控制流敏感:尊重语句的执行顺序
- 控制流不敏感:忽视控制流的顺序
java的数据类型可以分为值类型和引用类型;
- 基本类型也称为值类型,分别是字符类型 char,布尔类型 boolean以及数值类型 byte、short、int、long、float、double。
- 引用类型则包括类、接口、数组、枚举等。
Java 将内存空间分为堆和栈。基本类型直接在栈中存储数值,而引用类型是将引用放在栈中,实际存储的值是放在堆中,通过栈中的引用指向堆中存放的数据。
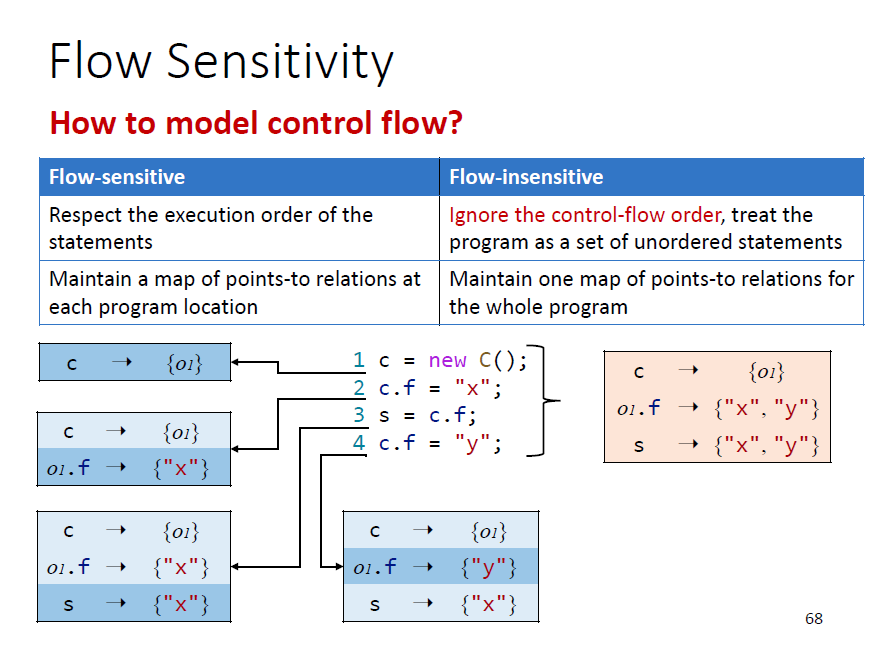
右边是flow不敏感分析的结果,目前主流是flow insensitive(对精度影响不大)
Analysis Scope
回答应该分析程序中的哪些部分
- 所有程序
- 需求驱动的分析:计算量更小;效率差异可能不够明显,仅满足特定需求
- 如果有多个client的需求,可能会有重叠,不如进行全程序分析效率高


Concerned Statements
只关心影响与指针有关的语句

- 本地变量:x 数量最多
- 静态field:C.f 和变量类似,不是重点
- Instance field:x.f 对象的field
- 数组元素 Array[i],一般会忽略index,静态分析无法得到,抽象成 只有一个field的对象,所有指都可以能取到,因此和instance field类似了
结论:学会1 3即可(不是

主要是5条语句



Pointer Analysis Foundations 1

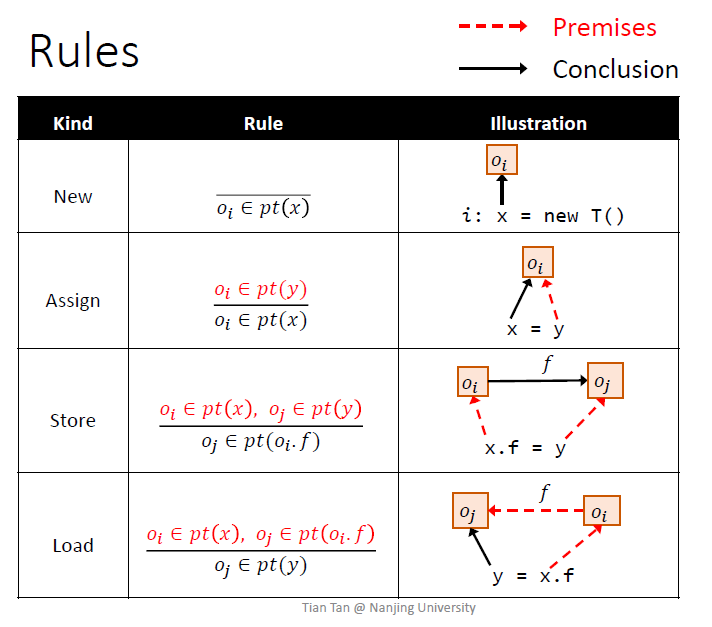
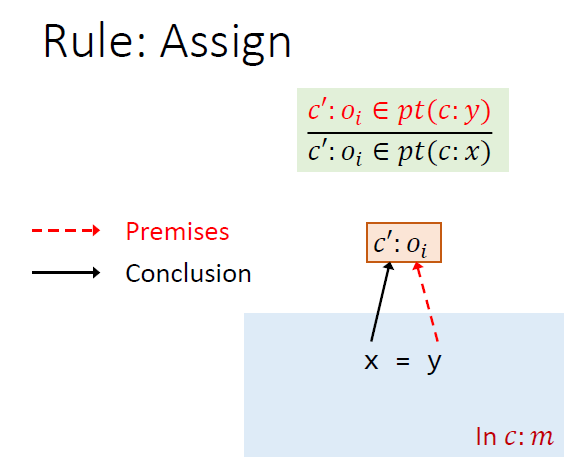
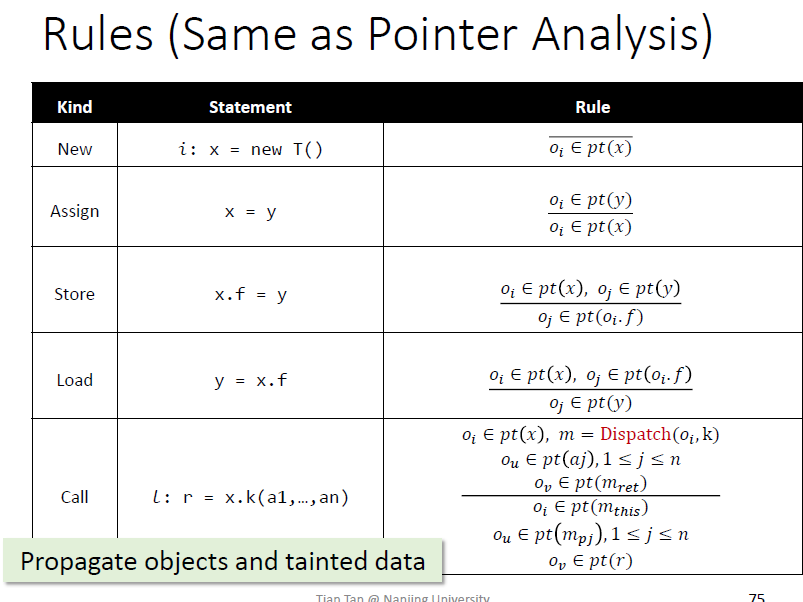
Rules
首先分析没有方法调用的程序(前4条语句),再学习如何处理方法调用

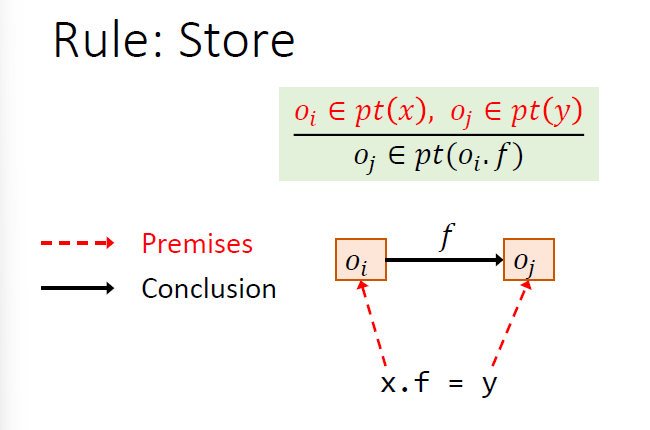
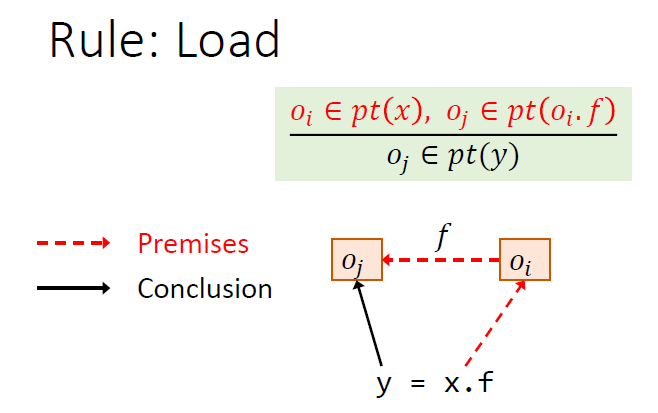
规则是推导式的,$pt(p)$指的是p指向的对象

new是将$o_i$加入到$pt(x)$中去
赋值将$y$指向的加入到$x$指向的

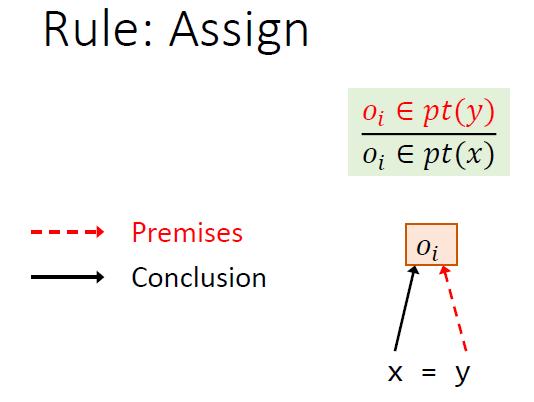
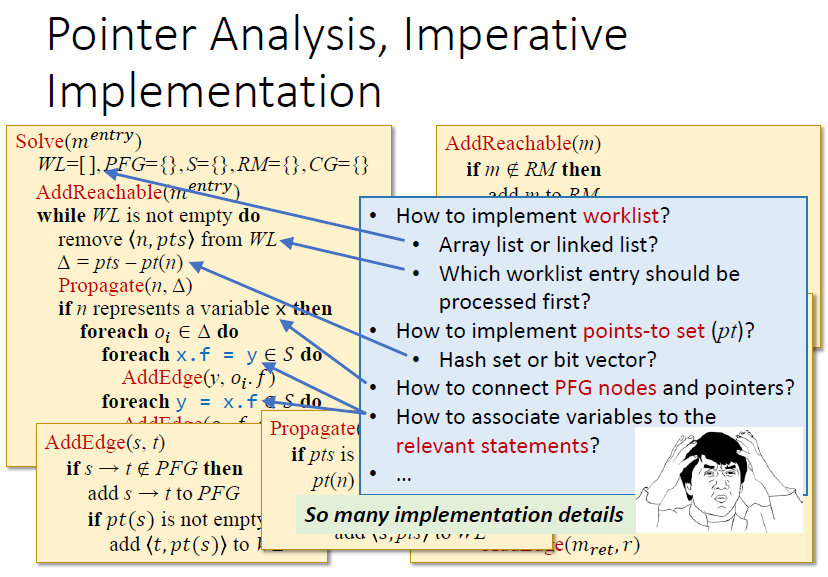
How to implement pointer analysis
本质上是将指针信息传播给其他指针,也可以理解为求解包含约束
指针分析的关键是当指针集$pt(x)$变化时,将变化传播给其他相关的指针
利用图来传播

指针流图pointer flow graph
有向图,表示对象如何在图中流动

边的含义是x的变化可能流向y
如何建立PFG的边?根据程序的语句的4条规则

c.f仅是一个指针表达式,不是一个指针,指针必须是对象

实现包括两步
- 构建指针流图
- 在PFG上传播指向信息
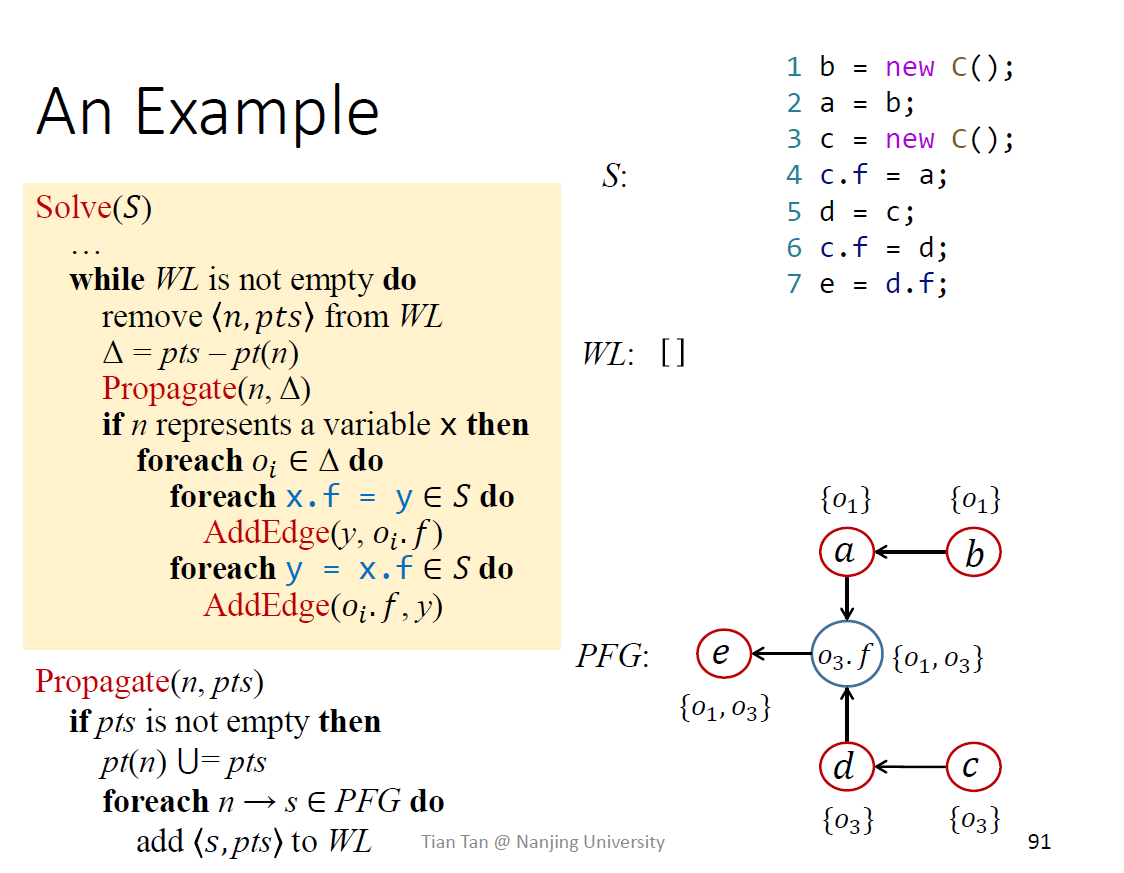
Algorithm
分别对应4个语句
S是要分析的语句的集合

WL包含了指针和指针集,是后续要分析的对象
简化只有2种语句
集合的减法是为了去重,去掉ptn已经有的指针



已经是union了为什么要去重?不影响正确性,但是可以跳过

另外两条对称的语句

可能有其他同类的不同对象已经连接了实例方法,因此是may引入新的PFG边
执行这个例子

Pointer Analysis Foundations 2
如何处理方法调用
过程间分析,需要call graph
与CHA方法对比,根据指针分析来确定call graph

实际上指针分析和call graph是一起构建的,on the fly
复杂起来了(
disptach:根据接受者对象和方法签名去找目标方法m,在做call graph
传receiver对象:$m_{this}$,OO语言很多操作通过this实现
- 传参:实参传给形参,变量之间连起来
- 传回返回值

solidity的dispatch只需要函数签名
问题:为什么this不加一个边?
连上会传递错误的信息,this只指向当前对象

实际的操作

从入口方法main函数进行分析,只分析reachable的方法,reachable对效率和精度有帮助

黄色部分是新增的步骤,和call graph相关

reachable方法
- 入口方法
- 出现新的调用边

为什么只处理new和assign,因为这两个语句不需要语境

为什么call graph存在$l\to m$就不再执行?实际上是对象的类型来决定目标方法的,虽然oi是新的对象,但是其他同类型的对象oj可能已经连过这一条边
这些判断条件存在的原因:为了实用性,减少不必要的操作
上下文非敏感,每个算法处理一次
算法的输出是每个变量的指针集以及调用图

例子,动笔自己写一写

和CHA的区别:更精确了



Pointer Analysis Context Sentivity
Java指针分析中对精度提升最明显的技术
动态执行时该程序时$i=1$
采用常量传播分析是NAC

需要上下文敏感的指针分析,每次调用id时对实参进行区分

Introduction
上下文不敏感为什么会不准确
- 动态执行时,一个方法可能在不同的语境下被多次调用
- 不同调用语境中方法的变量可能指向不同对象
- 不同语境下的对象 混合 并 传播 到了程序的其他部分
提高上下文敏感分析的效率

最古老和最著名的技术是call-site当做上下文,对调用栈的抽象

下节课介绍其他变种,后续介绍都是call-site
具体关注的是变量的上下文

上下文敏感 堆
- OO程序会频繁操作对象,heap-intensive
- 为了提高精度需要对 对象加上下文
- 粒度更细的抽象

为什么能提高精度?
动态执行时,每次调用都会创建新的对象
同一个语句,不同对象的操作可能不同

例子
动态执行指向n1,堆不敏感的程序分析指向n1 n2

有上下文敏感heap时,右边x.f语句会产生两个不同,意思是方法内对 对象的field也进行区分
如果没有变量上下文敏感,只做堆上下文敏感,相当于没做

都加上下文才能提高精度
Rules
先给出定义域和记号
程序的变量、对象都加上 上下文

策略决定c的内容,可以理解为一系列call-site
注意field没有,具体的实例的field有,因为通过对象来访问
指针也分两类,分别是变量和对象的;因此表示方式是两类的并
具体实现指针分析器需要利用这些规则
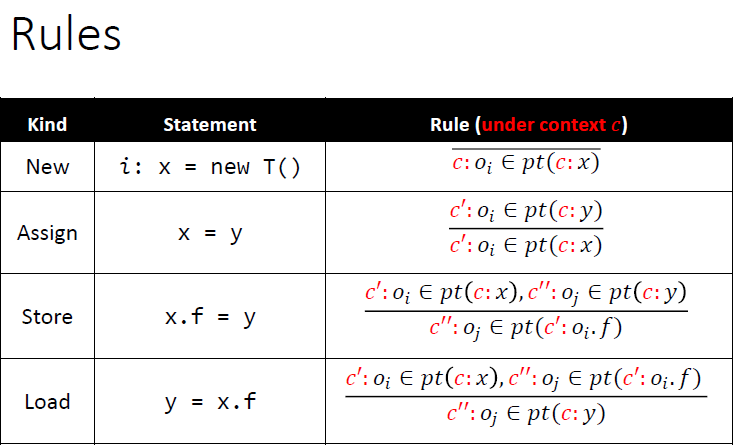
具体的理解
对于new语句,语境当中的规则:假设在方法m中,上下文是c,则给对象也加上下文
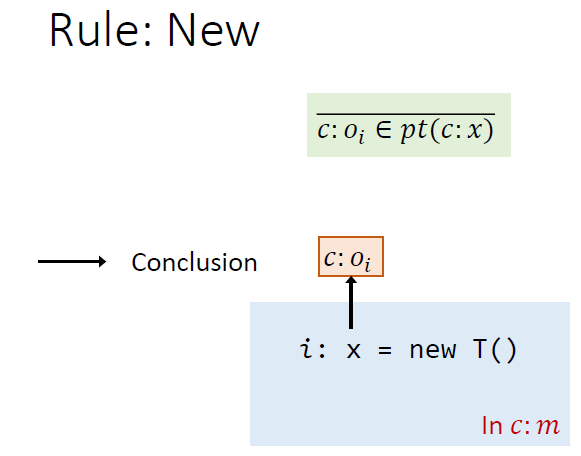
对于assign语句,比较直观
先分别取出x和y指向的对象,为什么不是同一个上下文c?
因为x和y的上下文相同,但是x和y指向的对象的语境不一定相同,上下文c和c‘可以相同
load和store对称
对于调用的规则,如何决定c
假设调用在某个方法里,当前的语境是c

- 先取出对象指向的上下文
- 选择对应方法,与上下文无关,取决于类型
- 选择上下文:为目标方法$m$选择上下文,根据当前调用点$l$能得到的信息
- 具体怎么选,请看下集
- 传receiver object
- 传返回值

好像是直接用了L?考虑如果在例子外面套个循环,就需要一个方法select进行选择了;除了还有其他的表示方法
$c^t$ 是新的一个上下文

目前Java流敏感分析的效果不够好
Algorithms
算法有两部分,构造PFG,在PFG上传播指针信息


区别在于每个节点表示的都是上下文敏感的变量或者field,节点额外带有上下文,笛卡尔积多了一个维度

连边就根据4条规则
对于call比较复杂,方法dispatch,传参数,this不连边,传返回值

打码之后和上下文不敏感的算法几乎一样

首先看solve算法

下面的集合也带有上下文信息
比如RM foo在ct下可达
CG也是上下文敏感的call-site和callee都有上下文,$c\to c^t$
入口函数的上下文为空
同一个call-site,目标函数内的context是一样的

Addedge和Propagate和CI分析一致
Variants
其他技术
给出select函数的定义
最常用的三种上下文敏感的变量
- call-site敏感
- object敏感
- type敏感

如果是上下文不敏感,可以看做是上下文敏感的特殊情况,select返回为空

每个context包括一系列的call-sites,将call site加入到caller,类似于调用栈,也叫call string,K-CFA(k-Context-Free Analysis)
call site sentivity

怎么得到当前的代码行数呢
递归调用的时候(方法调用自己),会出现无穷多次call-site

因此需要一个深度$k$,限制上下文的长度为$k$,一般$k\leq3$,会合并连续相同的callsite然后取队列末尾的$k$个

上下文层数越多,精度越高,一般是至少2层

分析x.get具体指向的方法
动态的理解:会返回1
静态分析:得到One.get()

利用调用点区分了14和15两个调用,如果是CI分析

object sensitivity

另一种表现形式的select,根据receiver object和heap context来区分

this指的是上下文本身(对象)
和1call site进行对比

换成2 call site能区分
object是否一定比call site好呢
this一样,调用的方法也一样

- 一般情况下精度是不可比较的
- 但是对Java这种OO语言,object更准确
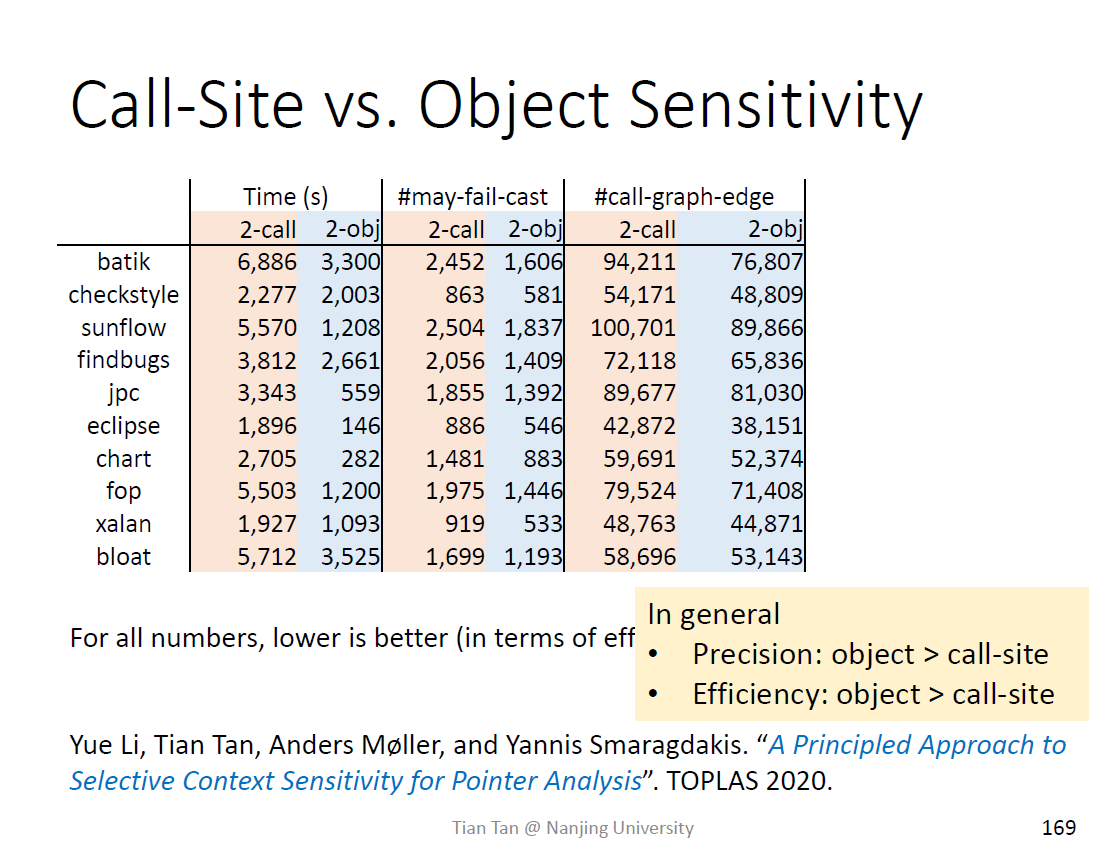
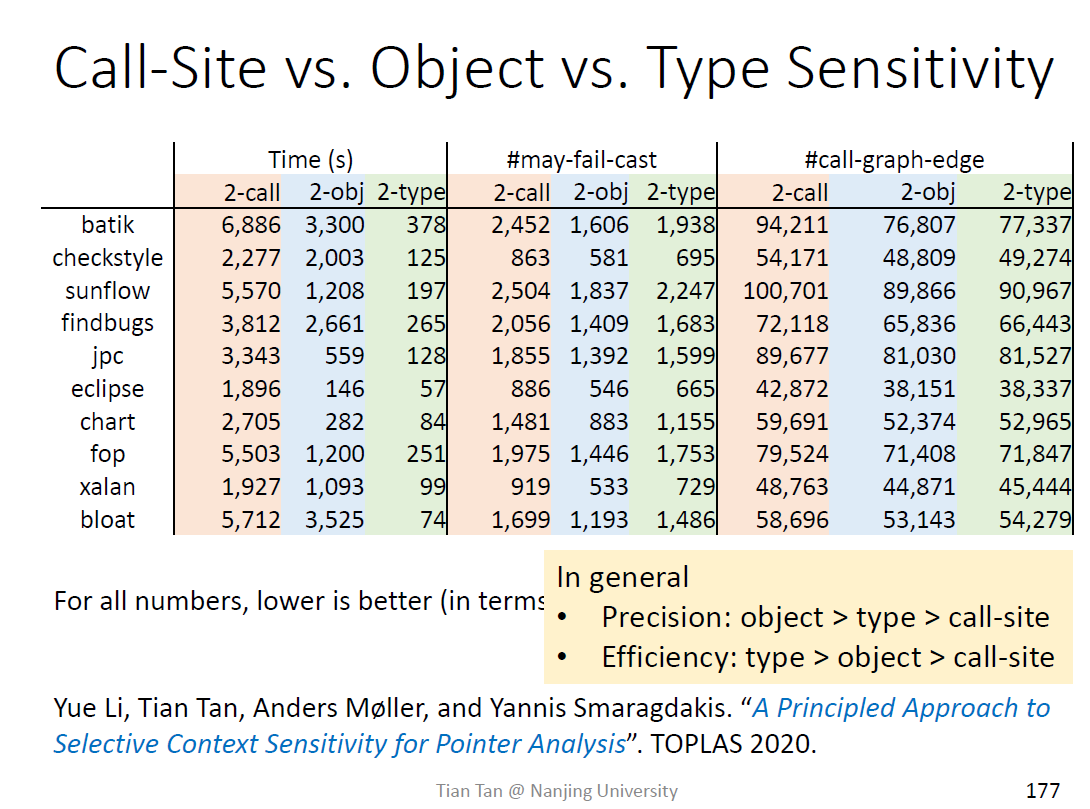
type sensitivity
实际上是对object的抽象

InType得到的不是生成的对象的类型,而是语句所在类
精度不如对象敏感技术,牺牲了精度换取速度


Security
抽象什么是安全:在敌手存在时达成某个目标

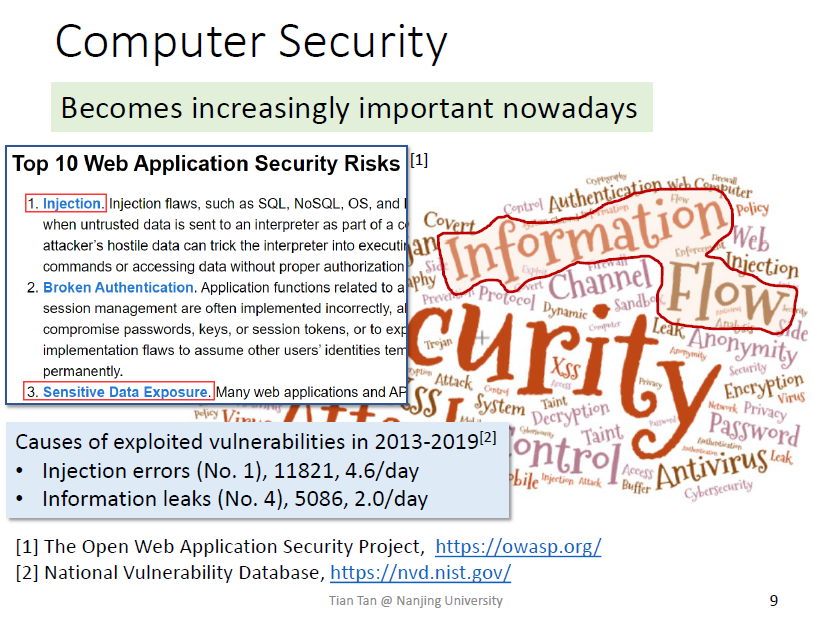
美国的NVD发现最多的漏洞是injection
injection和leak实际上是一类问题,信息流
Information Flow Security
目标:阻止不必要的信息流
- Access Control:标准方法,检查是否具有权限来访问特定信息;考虑信息是如何被处理的
- 得到信息后如何使用?
- 信息流安全 end2end
- 跟踪程序如何安全地处理信息
- 考虑信息如何传播

信息论的定义
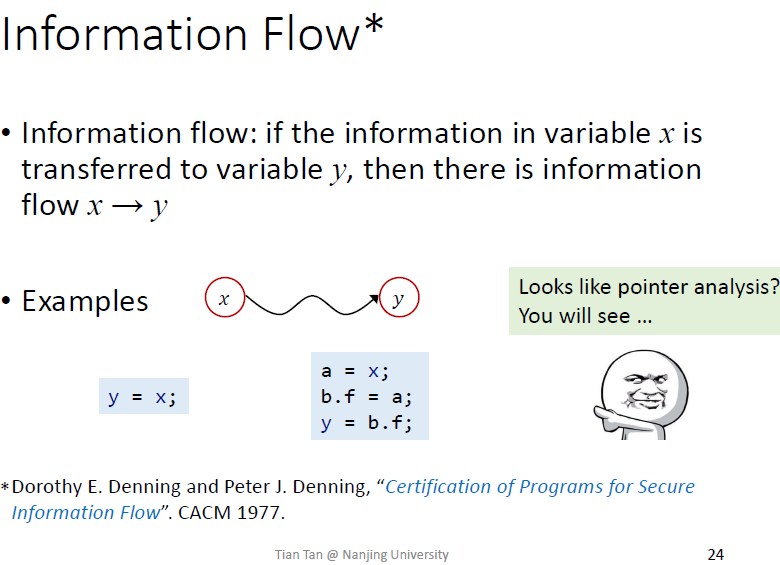
给变量分级
不同等级变量之间信息如何流动

最简单分法是2级分法(使用最广泛

可以利用偏序关系(格)来建模
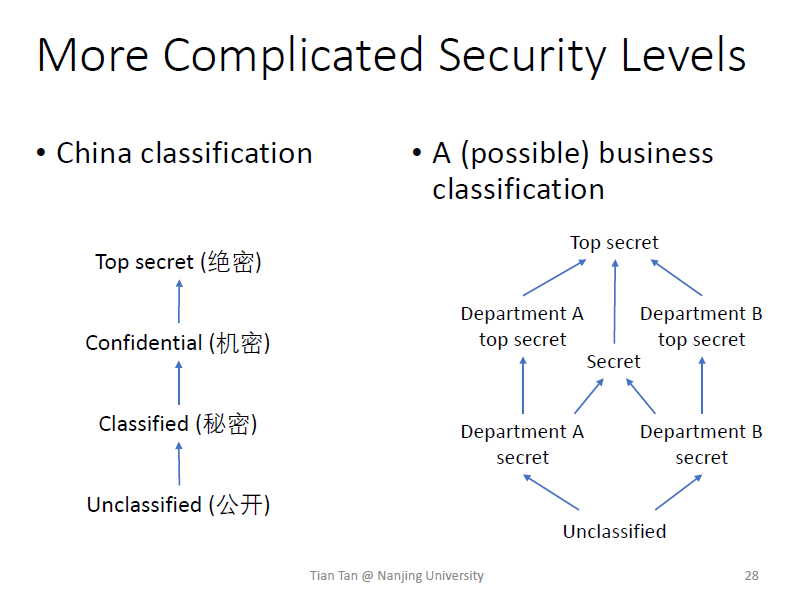
可以有比较复杂的level设置
policy:限制信息如何在不同密级之间流动

- 高级变量不能影响低级变量
- 通过观测低级信息无法推测出高级信息

Confidentiality and Integrity
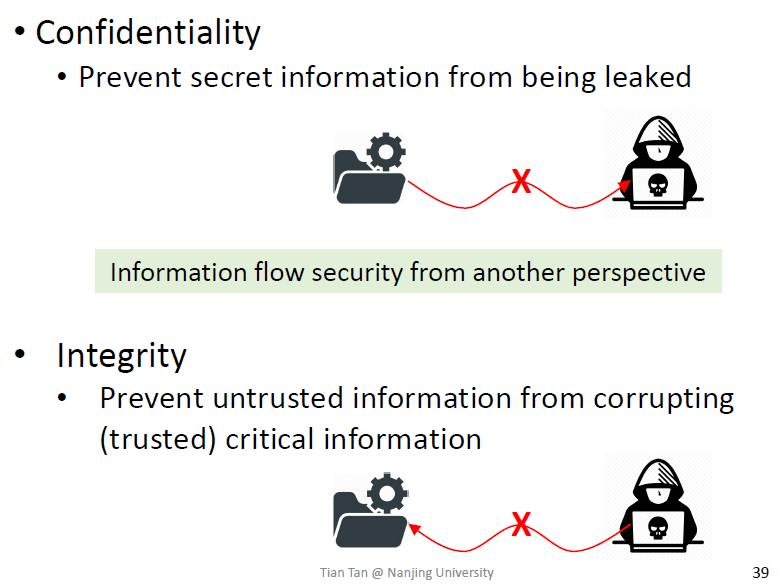
和密码学定义的Integrity不同,更像是真实性,外界信息的真实性

给US air force提出的问题
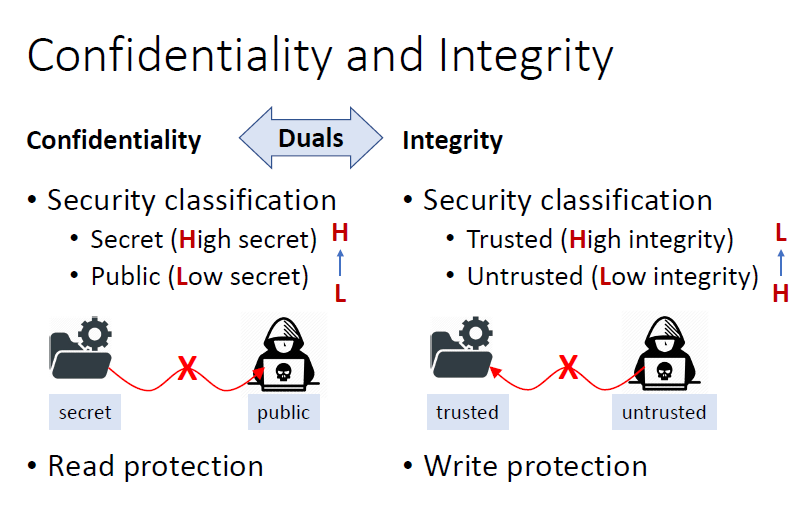
从完整性角度看,高级流向低级也不安全
扩展完整性的定义,之前的定义有点类似于正确性

数据流和信息流的区别:
数据流可以看做具体的数据
信息流更加抽象,广义,可以将数据流看做是信息流
Explicit Flows and Covert Channels

以上是显式流动
秘密可能作为条件语句的判断条件,称为隐式流

while循环 是一个信息流,但不是数据流

最后一个如果为负数,可能有error
统称上面这种类型为隐藏信道

还有侧信道,观察缓存命中率
总结所有类型的CC非常有挑战性
一般情况下,Cover Channel泄露信息有限

因此后续课程主要采用污点分析分析显式流
- 感觉后者更有意义
Taint Analysis
使用最广泛的信息流分析工具
数据分类
- 感兴趣的数据,label(同位素)
- untainted
污点数据来源于特定方法的返回值
关心污点数据是否会流动到特定的sink,一般是一些比较敏感的方法
是否存在从source到sink的流

应用
- 保密性: $\text{ secret data} \to \text{method}$
- 完整性:$\text{input} \to \text{critical command}$

两个性质的对称性
污点分析回答的问题
- 标记数据是否会流动到某个sink(sink的指针会指向标记的数据吗?)
两者是高度一致的,因此可以借助指针分析进行污点分析
- 将标记的数据视为特殊的object
- source是allocation site
- 利用指针分析进行污点数据传播

首先扩展指针分析的定义域,污点数据是指针分析的子集

输入输出

规则
call:如果dispatch方法来自source,认为可能是需要污点分析的
后续的传播和指针分析一样

检查sink?调用sink方法时,参数是否是tainted

例子
java中都是浅拷贝
x和y是别名
方便debug


对于运算符重载,需要更复杂的机制设计

Datalog-Based Program Analysis
Motivation
命令式语言:
声明式语言:sql

实现一个复杂的指针分析,采用不同语言的区别
回顾指针分析的rules和算法

还需要考虑的细节
如果用声明式语言实现

可读性更强了
Introduction
声明式逻辑编程语言,Prolog的子集
曾经是数据库的查询语言
- 程序分析
- 网络协议
- 吹牛

没有控制流?没有函数
表达能力不够
data/predicate
事实
数据的表

元组属于data,真的,称为fact
谓词由Atom表示

原子可以判定真假
下面这个类型也是原子

Rules/Logic
制定了如何推导fact

,是逻辑与

如何理解规则

考虑所有组合,如果一个组合可以让所有子目标为真,head为真,包含所有为真的谓词
交换subgoal不交换结果


问题在于初始数据来源
EDB:程序运行前定义好的;不变;
IDB:根据Rules定义,程序的输出,head只能是IDB

表示 或
写两条语句或者采用;
优先级低

表示非采用!

否 是搜索所有情况吗
支持递归,能力强大的来源

如果没有递归,只能支持基本的关系代数

需要保证规则是safe,所有的变量是有限的
- 表是有限的,表取反就是无限的

取反和递归必须分开

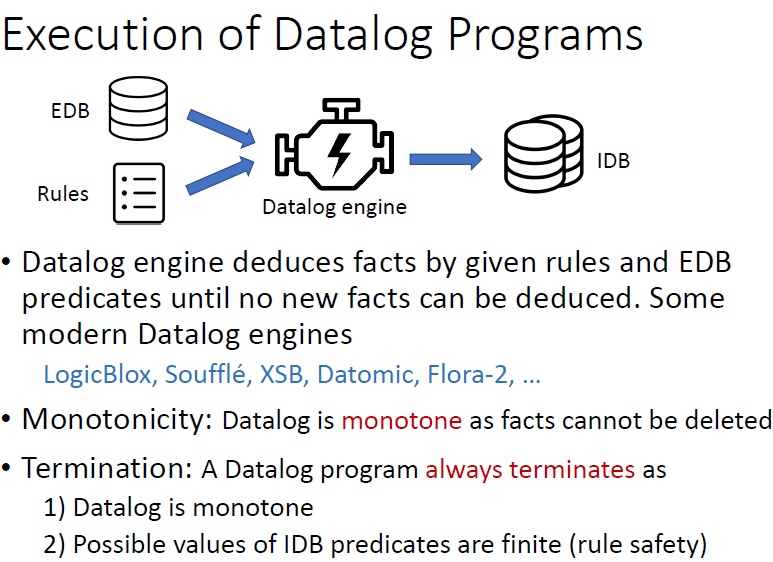
程序如何执行?engine
只能产生facts
Pointer Analysis
指针分析的EDB是语法分析可以直接获得到的信息
IDB是指针分析的结果

通过定义域定义4类语句
IDB只有2类,变量指向和fields指向


程序的可读性非常强,代码实现很干净

首先运行New,因为varpoints都是空
将整个New复制到Varpointsto

终止条件:不再能产生新的facts
如何处理函数
引入新的谓词 EDB和IDB
k应该包含参数信息,不然无法处理多态
和之前类似,传4部分信息

增加对入口方法的处理即有了全程序分析

Taint Analysis
在指针分析的基础上,修改EDB和IDB


_是因为不关心当前的下标
优势和劣势

- 简洁、可读性强
- engine优化,效率高
缺点
- 表达性受限,不是图灵完备
- 如果需要删除facts,无法实现
- 对于all的逻辑不是很好表达
- engine是黑盒,无法自行优化效率

CFL-Reachability and IFDS
context free language是IFDS的理论基础
利用图可达进行程序分析表达

放松心态,学懂50%就算成功!
Feasiable and Realizable Paths
存在一些路径是不可达的
希望程序分析尽可能不被这些不可达路径污染,然而静态分析中这个问题是不可判定的
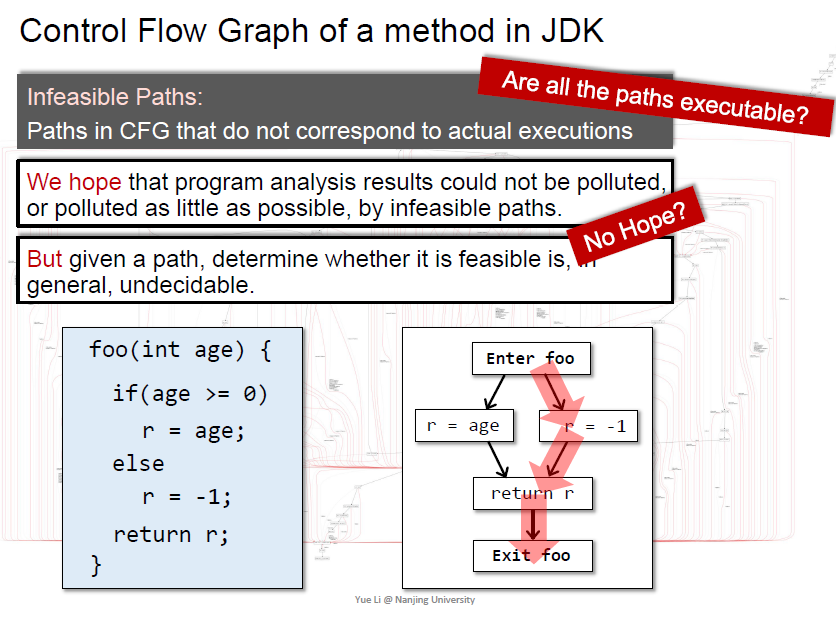
红色路径是静态分析无法避免的错误
绿色路径可以通过上下文敏感避免
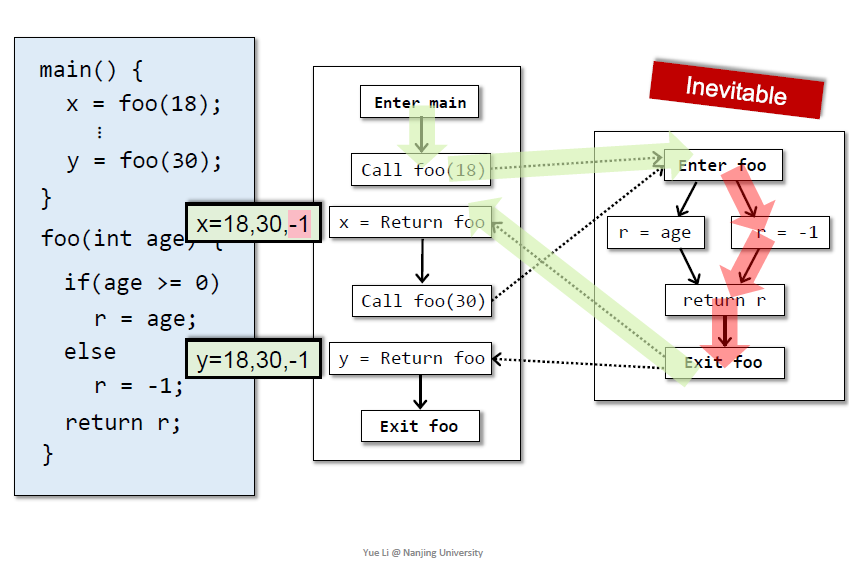
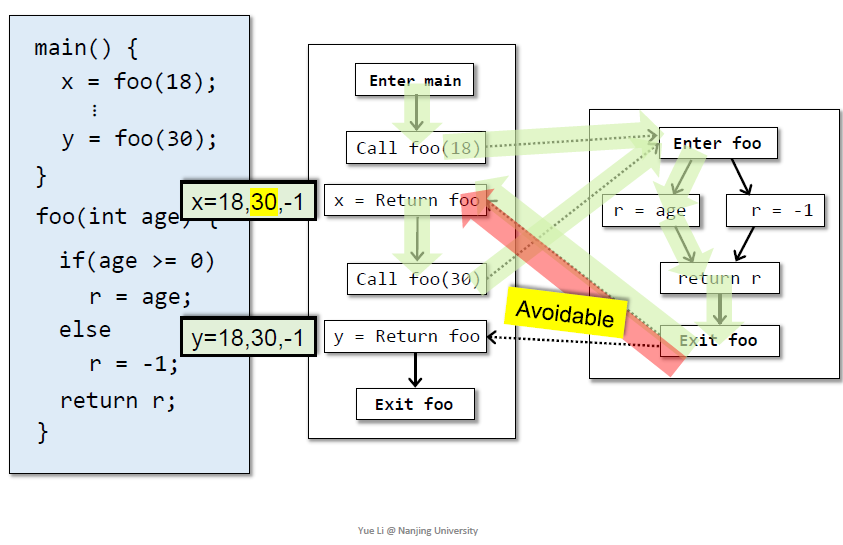
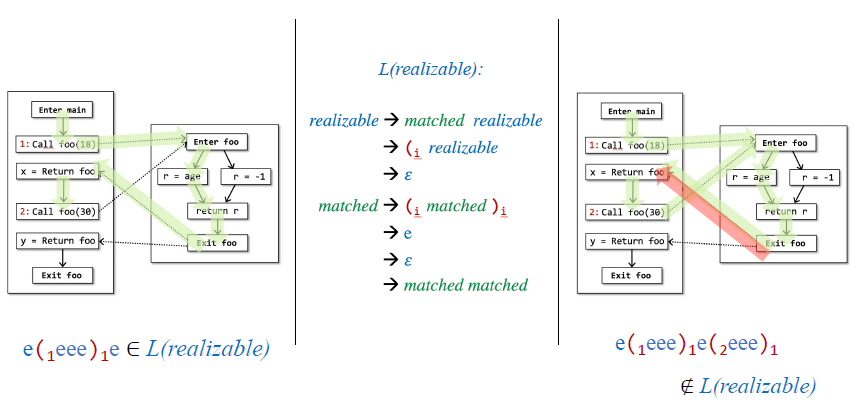
realizable path:跨函数调用的返回应该和call匹配
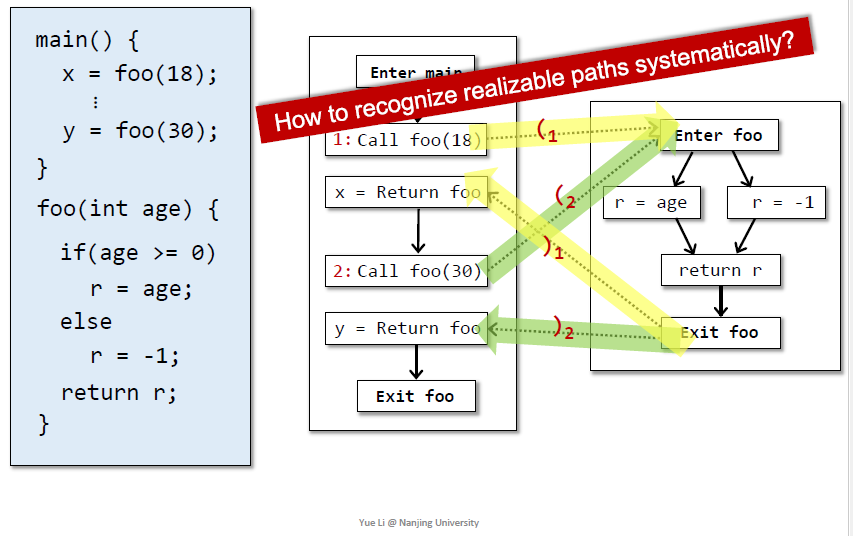
unrealizable一定是不会执行的,如何识别

括号匹配,太复杂就不适用,寻找系统的方法
CFL-reachability
上下文无关文法生成的是上下文无关语言
没学过编译但学过计算理论

编程语言文法一般是CFG

部分 括号匹配
有右括号一定有左括号,反之不一定成立(call了不一定return)
通过call-site进行括号的索引
如何形式化括号匹配的问题?写CFL的语法
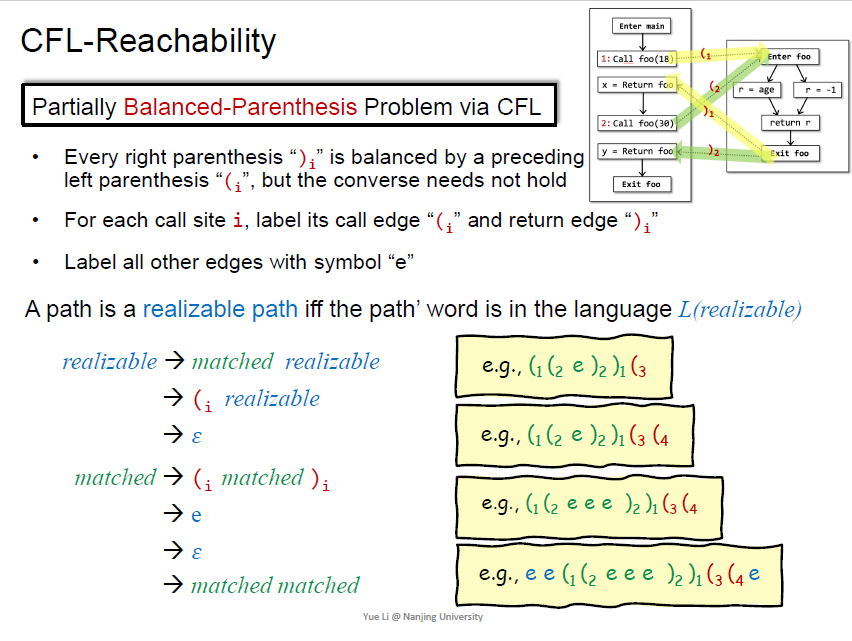
从规则来看,没有单独产生右括号的规则
IFDS

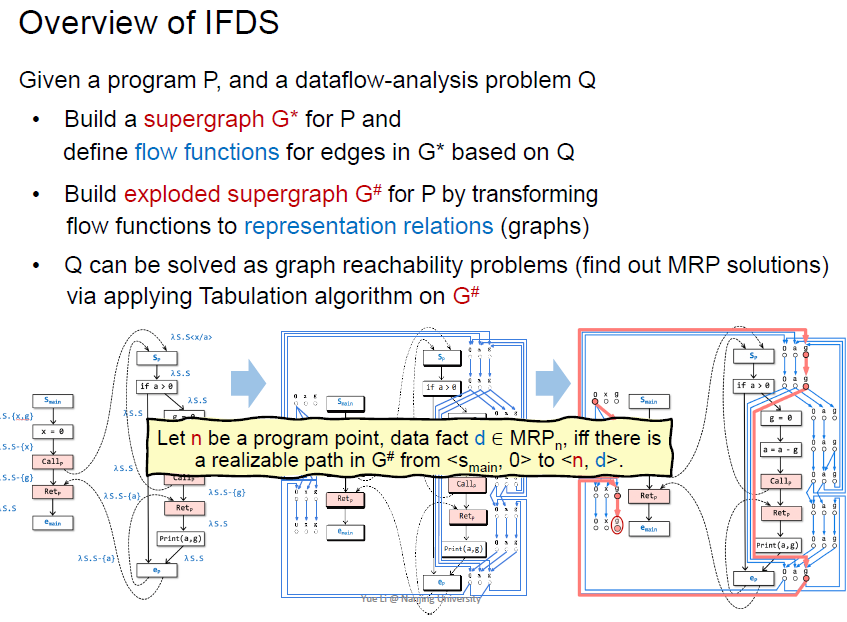
可以通过图可达性来表达的图分析算法
不再是迭代式算法,用图的方式(没有传播的过程)
过程间的 有限 可分配的 子集问题
定义域有限 流函数是distributive

具体可以认为是先meet再transfer和调换顺序结果一致
回顾MOP,利用IFDS能够给出MRP

是所有edge上的f的复合函数
MOP是把所有path的结果并起来
MRP只考虑realizaable path(返回边和callsite对应,不能返回到之前已经返回过的边),不再沿着假的边去分析,可能更精准
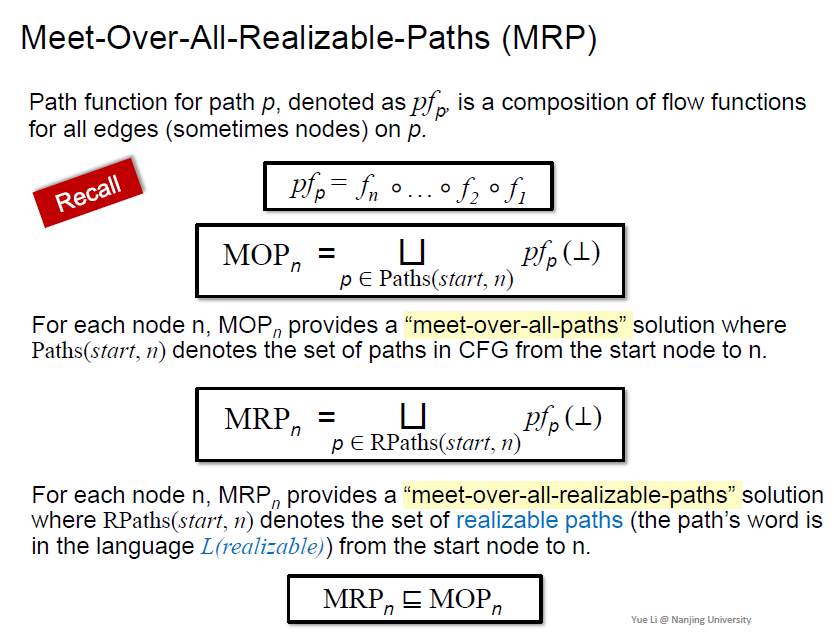
显然是MOP的子集
构造supergraph,定义flow func
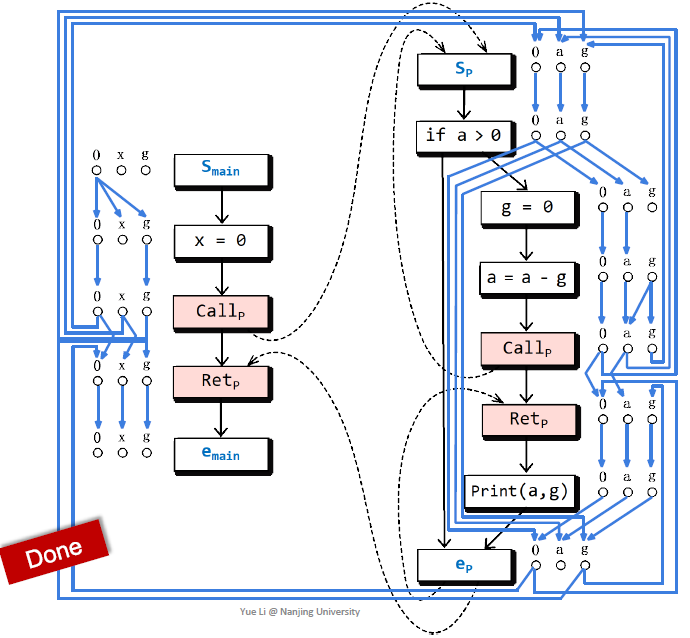
构造explded supergraph
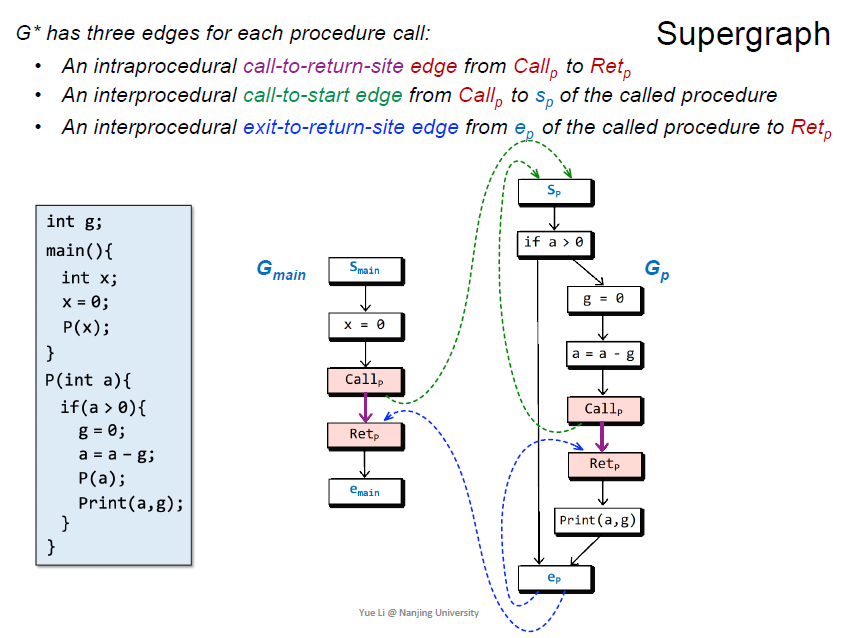
$G^*$由一系列的$G_{main}$和$G_p$组成
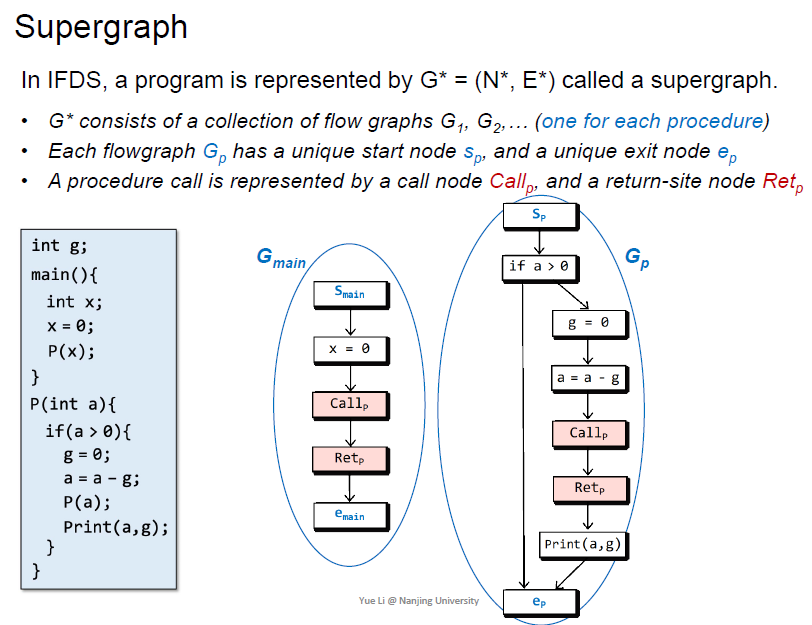
每个call site都有3条edge
flow function的设计采用 可能未初始化的变量 的设计
具体的函数形式为lambda表达式
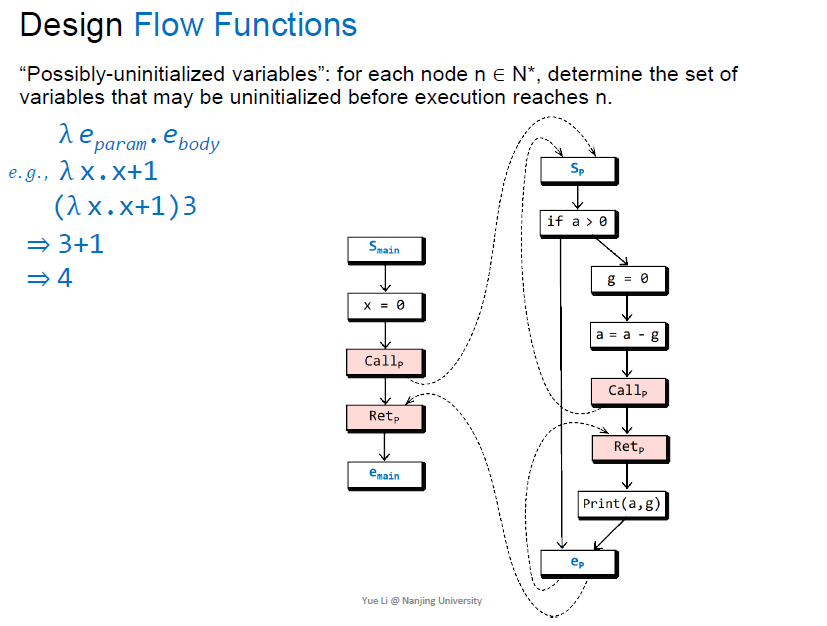
lambda表达式类似于匿名函数,$\lambda e_{param}\cdot e_{body}$
无论输入,输出$x,g$
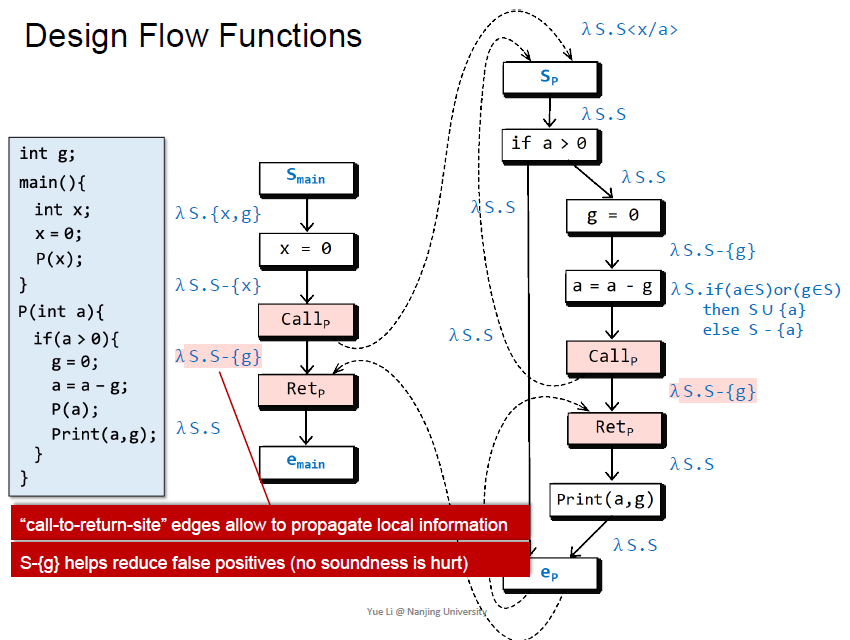
S是所有没有被初始化的值
$\lambda \ S.{S-x}$
减去g为了提高精度,真实情况不会有这条边,增加这一条边传播了本地变量的信息
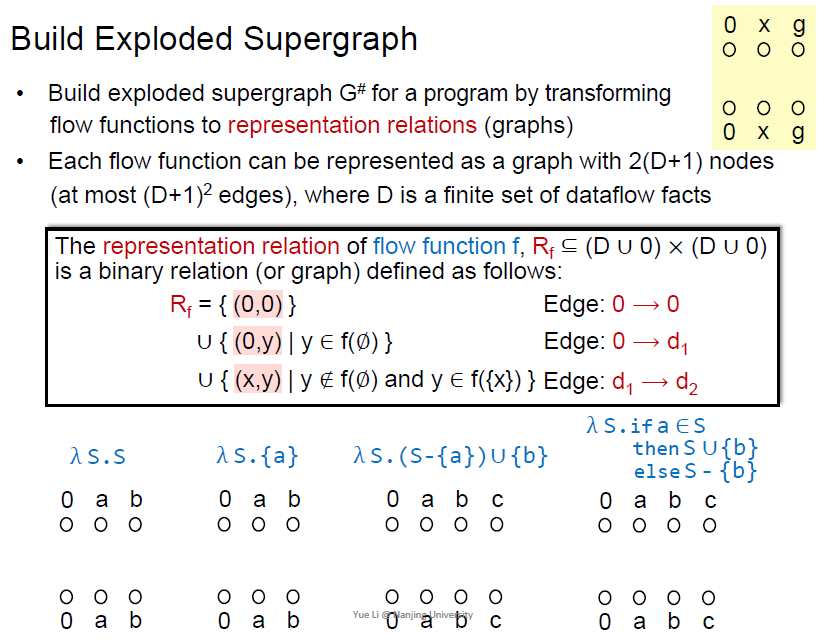
有了supergraph之后,建立exploded supergraph,拆分了flow function
D=2

和传统的程序分析的定义区分,之前通过n4的out来判断存在
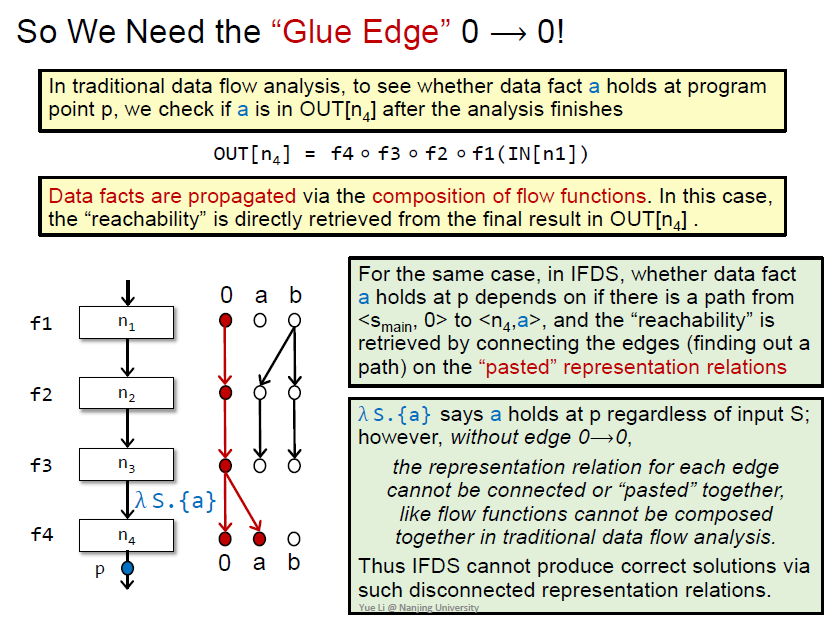
利用tabulation算法判断可达性
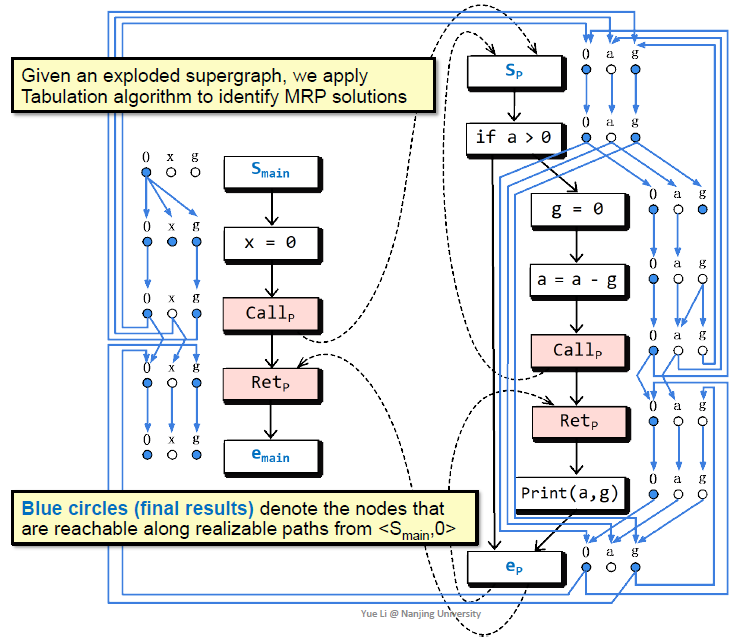
如果d可达就涂成蓝色
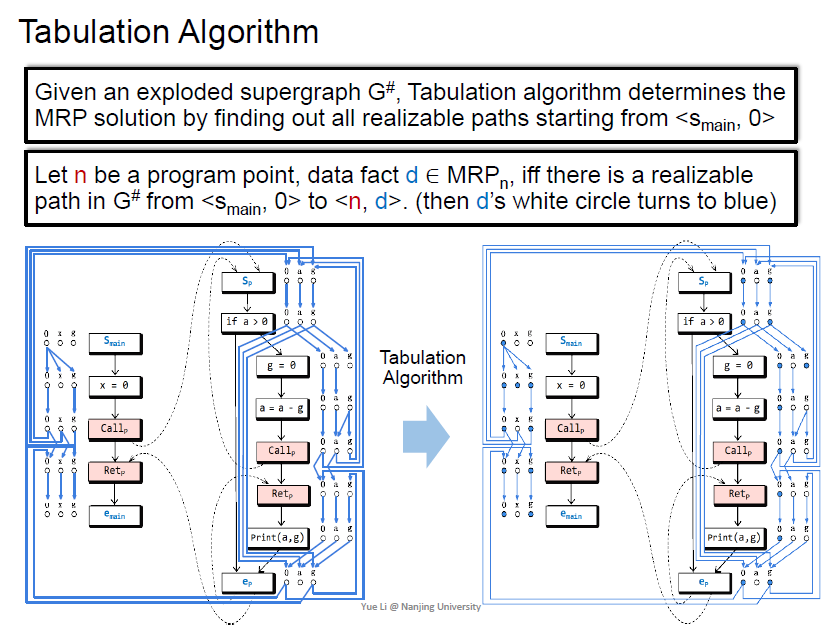
这个算法比较复杂,不做详细介绍

E是边的个数,D是domain size
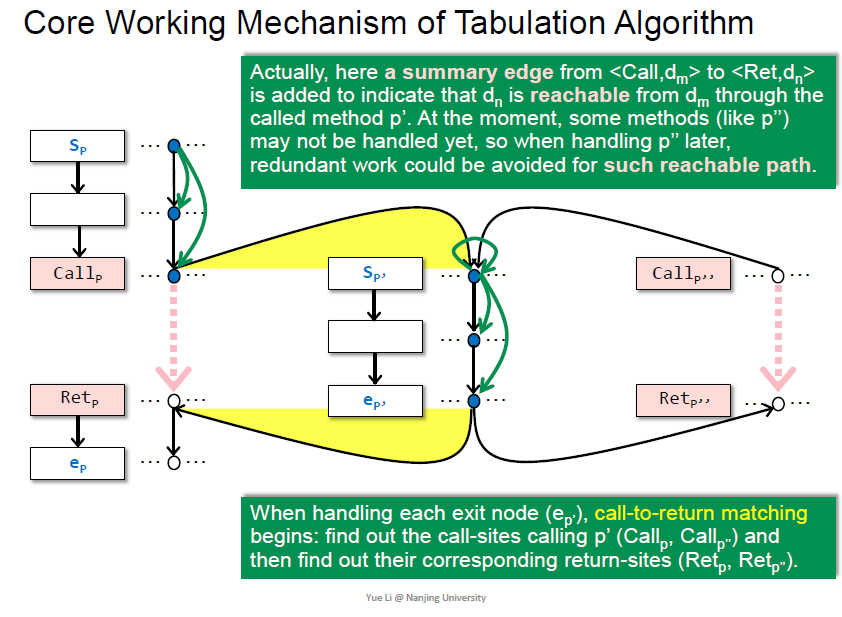
处理exit节点时, 找到对应的call边
额外还有call到return的 summary edge,加速
可分配性的理解

具体问题能够利用IFDS解决需要用可分配性判断
IFDS的flow函数只能处理一个元素

如果需要多个输入事实来判断能否产生正确的输出,不能用IFDS
最后的两个例子可以用IFDS
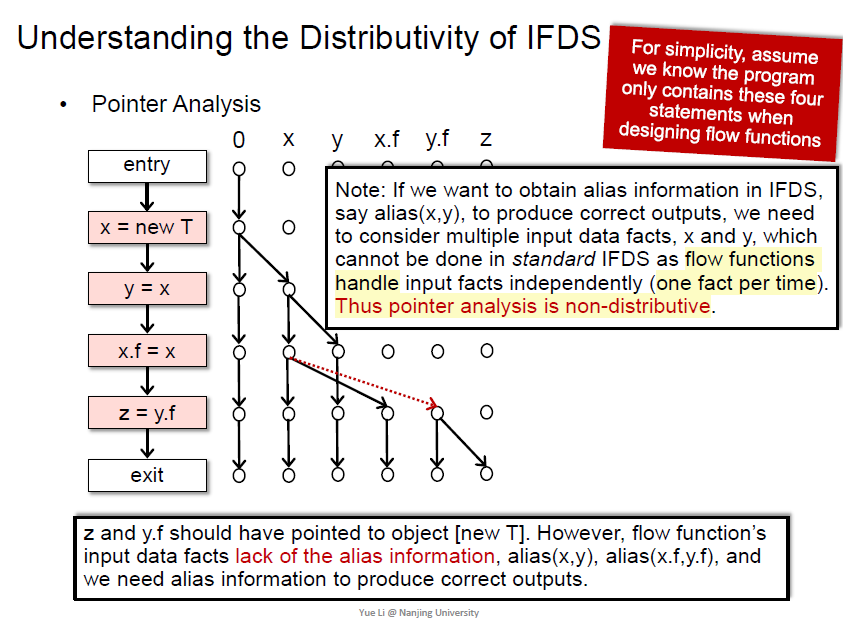
x,y,x.f指向o,正确吗

缺少别名信息,这个信息同时需要x和y,因此指针分析不能用标准的IFDS

Soundness and Soundiness
程序分析约有50年,soundiness是2015年提出的
前沿的话题
soundness
保守的近似,近似所有可能的程序行为
- 学术界:分析真实程序语言编写的完整的程序,没有sound
- 工业界:所有工具都不得不牺牲soundness

每个编程语言存在的难以分析的feature
比如js的eval,c对指针加减

因此现在论文的结果可能声称是sound,对hard one是unsound;
或者忽略
不分析会导致严重的结果吗?Java

soundiness指真实的程序没法分析一些困难的语言的特征
大佬振臂高呼,提soundiness


三类概念的区别
为什么下面的两类很困难
Hard Language Feature: Java Reflection
对java和安卓分析的噩梦,notorious

为什么难分析
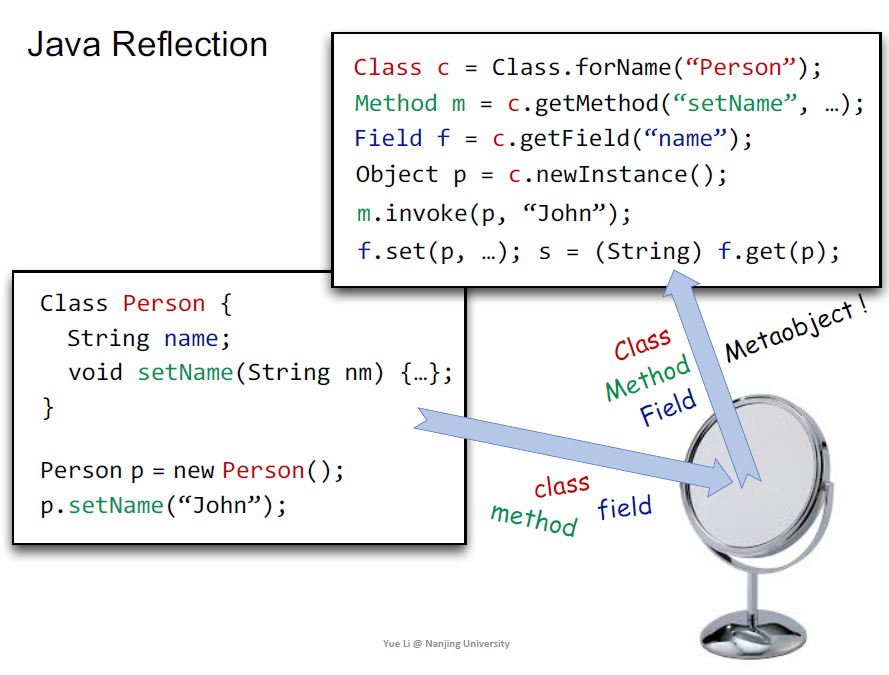
在Java编程语言中,反射(Reflection)是指在运行时动态地获取、检查和操作类、对象、方法和属性的能力。它允许程序在运行时通过名称来获取类的信息,调用方法,访问字段,创建对象等,而不需要在编译时明确地引用类或方法。
Java反射提供了一组类和接口,如Class、Method、Field等,用于在运行时检查和操作类的结构。通过使用反射,可以实现以下功能:
- 获取类的信息:通过反射,可以获取类的名称、父类、实现的接口、构造函数、方法和字段等信息。
- 动态创建对象:通过反射,可以在运行时通过类名创建对象的实例,而无需提前知道类的具体类型。
- 调用方法:通过反射,可以在运行时调用对象的方法,包括公共方法、私有方法和静态方法。
- 访问和修改字段:通过反射,可以在运行时访问和修改对象的字段(即成员变量),包括公共字段和私有字段。
- 操作数组:通过反射,可以动态创建、访问和修改数组对象。
反射是运行时行为
为什么需要分析呢(应用在哪里,松耦合,编程更灵活)
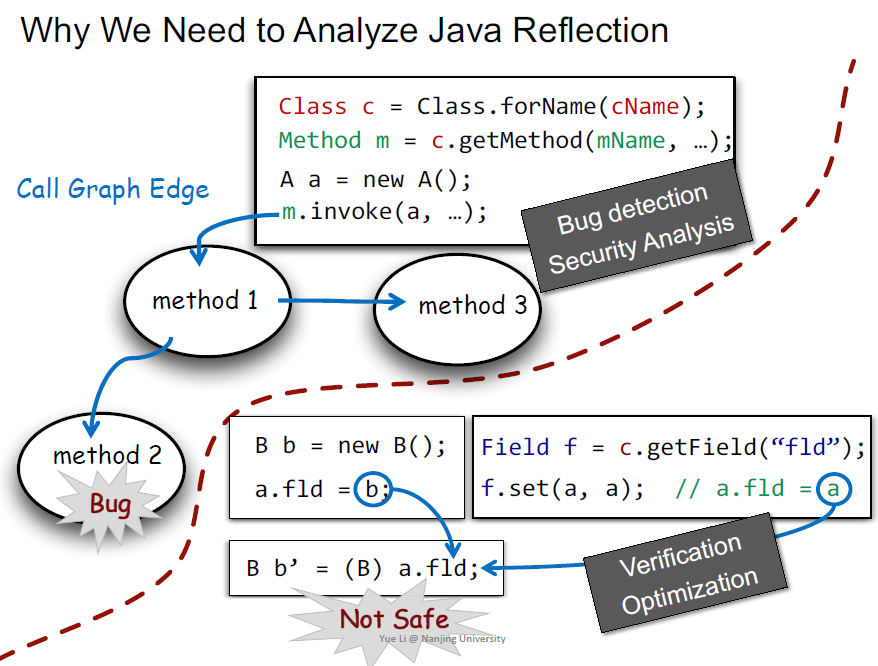
右边这个例子可能是错误的

分析反射的技术:字符串分析+指针分析
直观的想法
存在的问题:这些变量可能是从文件中读入的;编码过的

李老师和谭老师的工作绕不过去
类型推理+字符串分析+指针分析
在调用的时候利用参数来推理


目前最新的工作也是他俩做的
第三类方法,利用动态分析的结果,依赖于test case,给出的都是真的

Hard Language Feature: Native Code
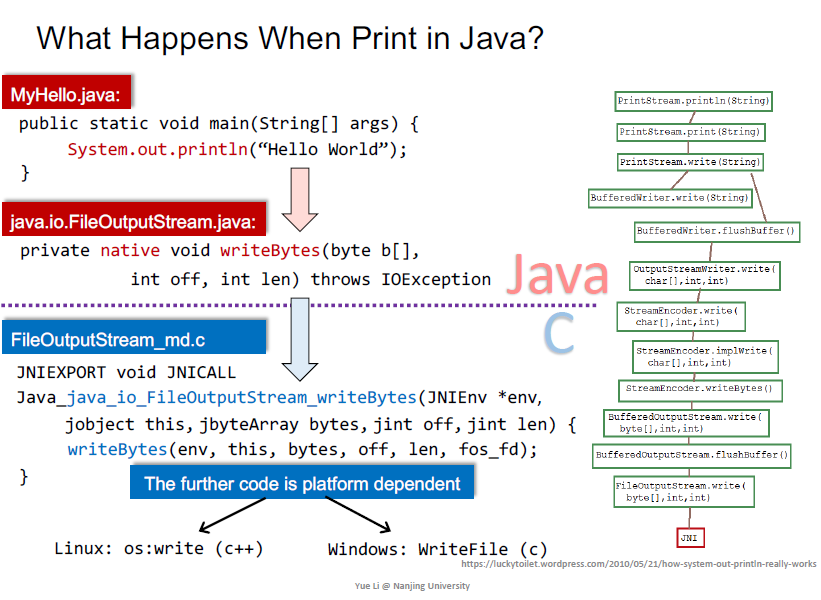
native声明指方法由外部语言实现的,如跨语言调用C/C++
JNI
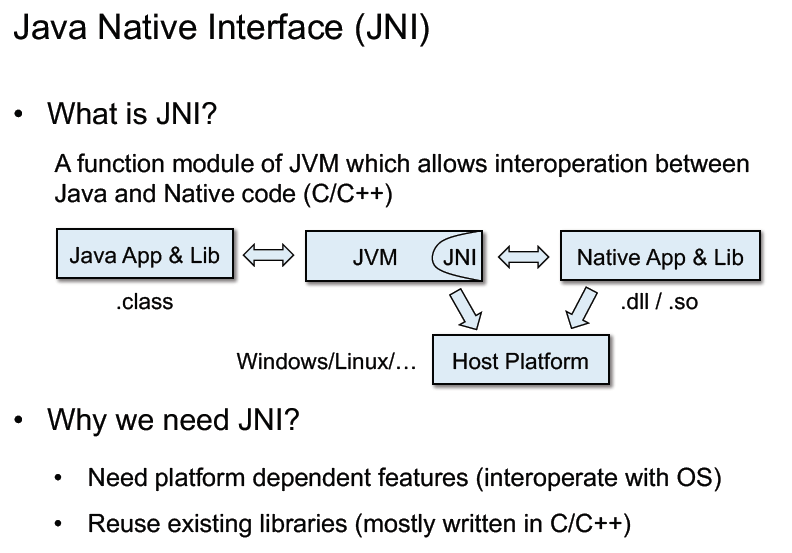
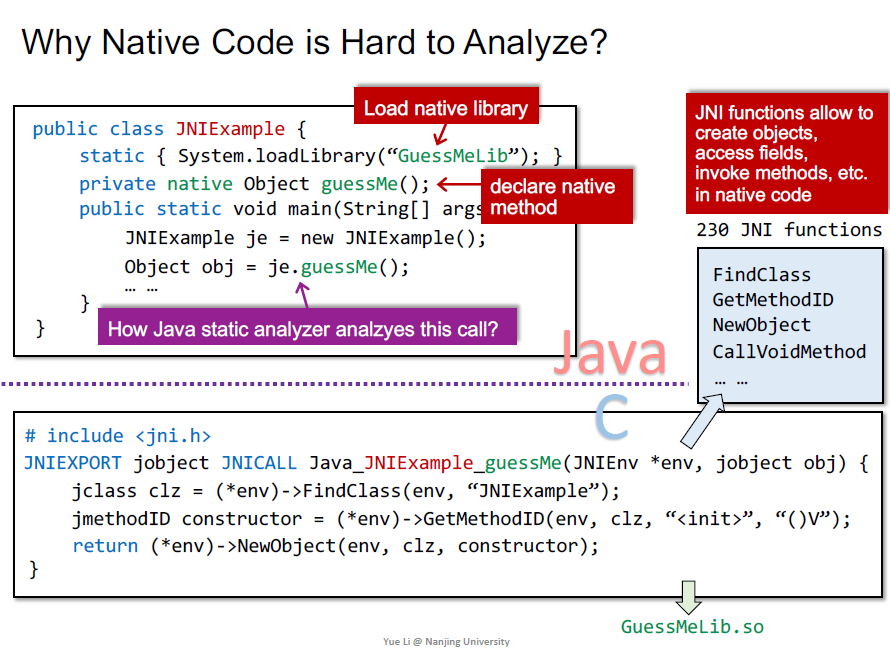
现在的解决方案:
- 手动建模native code
- 用java简单模拟一下功能
- 大概比java实现快一个数量级
- binary分析